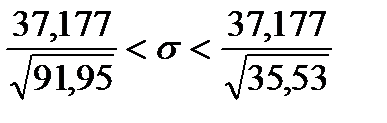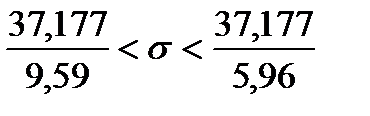Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Результаты вычисления интервальных оценок для математического ожидания и дисперсииДля вычисления интервальной оценки математического ожидания воспользуемся формулой:
где а = М(Х) – математическое ожидание, tn−1,p – процентная точка распределения Стьюдента с n-1 степенью свободы; p – доверительная вероятность. Подставляем в формулу вычисленные ранее значения
Задаёмся доверительной вероятностью Для каждого значения
При
Доверительный интервал для а = М(Х) имеет вид: 40,9403 < a < 43,4397. При
Доверительный интервал для а = М(Х) имеет вид: 40,528 < a < 43,852 Для интервальной оценки дисперсии существуют следующие неравенства:
Подставляем в неравенство известные значения N и
Задаваясь доверительной вероятностью
Для
Подставляя в неравенства
16,609
Для
Подставляя в неравенства  15,047
Для интервальной оценки среднего квадратического отклонения имеем
При
При
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 310. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
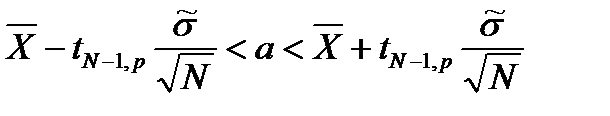 , (1.11)
, (1.11) ,
, 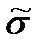 и N. В результате получим:
и N. В результате получим: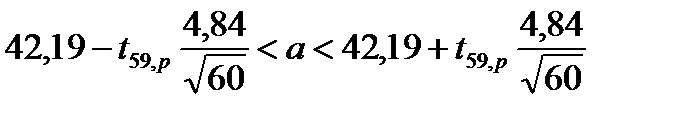
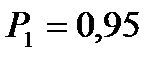 ;
; 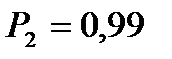 .
.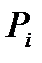 (i=1,2) находим по таблице (приложение А) значения
(i=1,2) находим по таблице (приложение А) значения 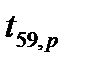 и вычисляем два варианта интервальных оценок для математического ожидания.
и вычисляем два варианта интервальных оценок для математического ожидания.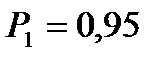 находим
находим 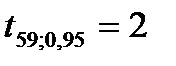
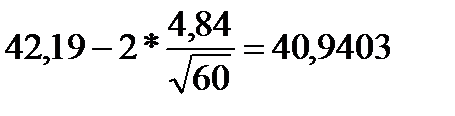
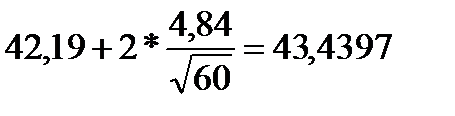
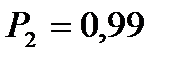 находим
находим 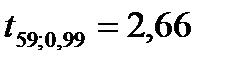
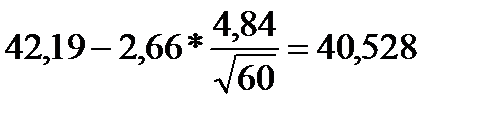
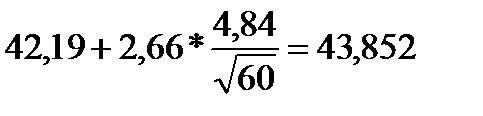
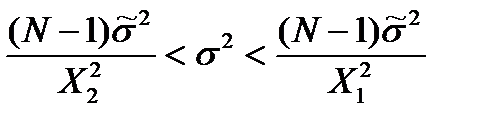 (1.12)
(1.12) получим неравенство, в котором неизвестны
получим неравенство, в котором неизвестны 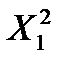 и
и 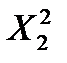 .
.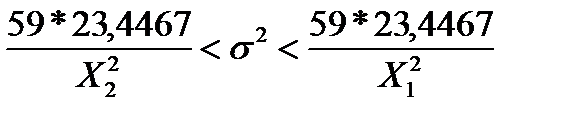
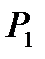 (или уровнем значимости а) вычисляем значения
(или уровнем значимости а) вычисляем значения 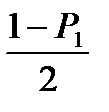 и
и 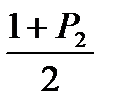 . Используем эти два значения и степень свободы V=N-1 по таблице находим
. Используем эти два значения и степень свободы V=N-1 по таблице находим 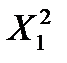 и
и 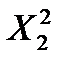
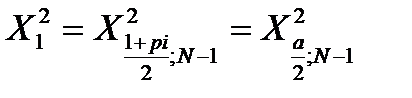
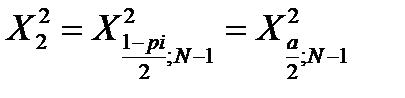
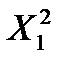 и
и 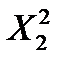 - это границы интервала, в который попадает случайная величина Х, имеющая
- это границы интервала, в который попадает случайная величина Х, имеющая 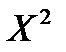 распределение вероятности
распределение вероятности 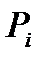 и заданной степени свободы V.
и заданной степени свободы V.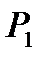 =0,95, (1 – р1)/2 = 0,025, (1 + р1)/2 = 0,975 и V=59 находим по таблице (приложение Б):
=0,95, (1 – р1)/2 = 0,025, (1 + р1)/2 = 0,975 и V=59 находим по таблице (приложение Б):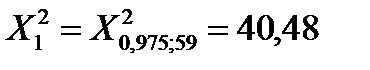
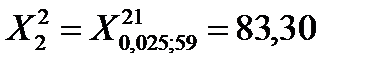
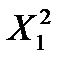 и
и 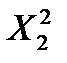 и произведя вычисления, получим интервальную оценку:
и произведя вычисления, получим интервальную оценку: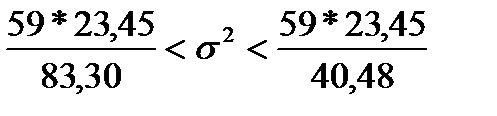
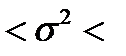 34,179
34,179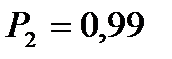 ,
, 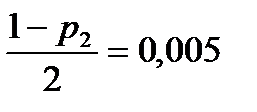 ;
; 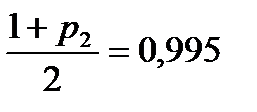 и V=59 находим по таблице приложения Б:
и V=59 находим по таблице приложения Б: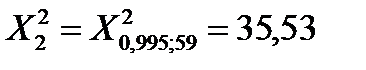
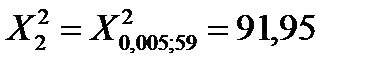
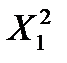 и
и 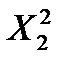 и произведя вычисления, получим интервальную оценку:
и произведя вычисления, получим интервальную оценку: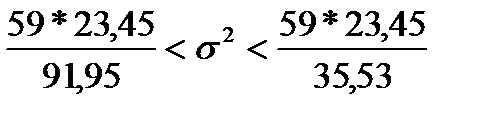
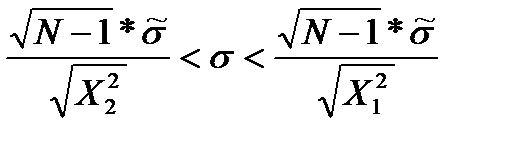 (1.14)
(1.14)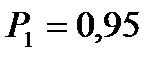 получаем доверительный интервал:
получаем доверительный интервал: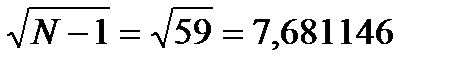
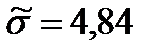
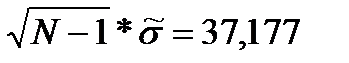

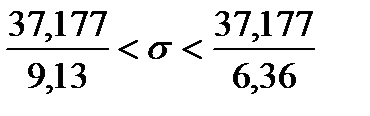
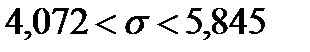
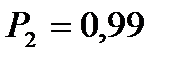 доверительный интервал:
доверительный интервал: