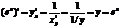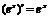Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
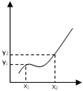
Обратная функция и её дифференцирование.⇐ ПредыдущаяСтр 19 из 19 Пусть дана монотонная функция y=f(x) (монотонно возрастающая или монотонно убывающая). Для определённости рассмотрим монотонно возрастающую функцию.
Тогда различным значениям аргумента х1 и х2 соответствуют различные значения функции: y1=f(х1) и у2= f(х2). Причём, это справедливо только для монотонной функции. Т.е. для монотонной функции существует взаимно однозначное соответствие между значениями х и y. Каждому значению y соответствует единственное значение х и в данном случае формально можно считать, то переменная х является функцией от y. X=φ(y). Эта функция X=φ(y) называется обратной по отношению к функции y=f(x) . Теорема: Если для функции y=f(x) существует обратная функция X=φ(y), имеющая в некоторой точке у производную φ’(y), то ф-ция y=f(x) имеет производную в соответствующей точке X=φ(y), кот. может быть найдена по формуле Доказательство: Дадим приращение ∆у, тогда переменная х получит приращение ∆х=φ(х+∆х)-φ(х). В силу монотонности f(x) и φ(х), ∆у≠0 и ∆х≠0. Т.к. в этом случае
Перейдём в обеих частях этого равенства к пределу при ∆х→0, тогда и ∆у→0. Имеем:
Обратные тригонометрические функции и их производные Функция y=sin x монотонно возрастает на отрезке При этом она изменяется на отрезке [-1;1]. Поэтому на отрезке [-1;1] существует обратная ей ф-ция, кот. обозначается x=arcsiny
Найдём производную. Пусть у=arcsinх, тогда х=siny. х’y=cosy, тогда Аналогично можно ввести функцию, обратную ф-ции y=cosx. Cos является монотонной ф-цией на отрезке [0;π]. Обратная ф-ция обозначается y=arccosx, определена на отрезке [-1;1]. 
Рассуждая аналогично, можно показать, что Функция у=tgx монотонна при
Ф-ция у=arcctgx, обратная по отношению к ф-ции у=ctgx, имеет производную, определяемую формулой.
Гиперболические ф-ции При решении многих практических задач ех очень часто встречается в виде некоторых комбинаций, для кот. используются специальные обозначения.
Между гиперболическими ф-циями справедливы многие соотношения, как с тригонометрическими ф-циями. ch2x-sh2x=1 Обратные гиперболические ф-ции: arshx, archx, arthx, arcthx. Производные от гиперболических ф-ций нетрудно найти, используя правило дифференцирования экспоненты.
56. Производные функций от lnx и ex Y= lnx
(lnx)’=
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 458. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
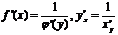

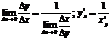 . ч.т.д.
. ч.т.д.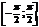 .
.
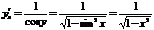 , таким образом
, таким образом 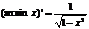

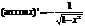
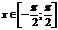 и определена на интервале (-∞;+∞); обратная функция y=arctg x определена на интервале (-∞;+∞).
и определена на интервале (-∞;+∞); обратная функция y=arctg x определена на интервале (-∞;+∞).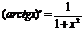
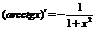
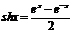 - синус гиперболический х.
- синус гиперболический х.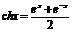 - косинус гиперболический х.
- косинус гиперболический х.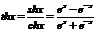 - тангенс гиперболический х.
- тангенс гиперболический х.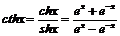 - котангенс гиперболический х.
- котангенс гиперболический х.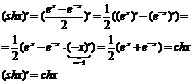
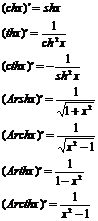
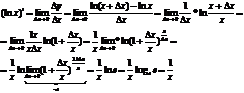
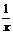
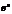 - обратная по отношению к функции lnx. Y=
- обратная по отношению к функции lnx. Y= 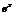 . X=lny
. X=lny