
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Простые модели сплошных средСамой простой моделью сплошной среды является идеальная жидкость. Она пригодна для описания жидкостей и газов с малой вязкостью. Для идеальной жидкости тензор напряжений задается в виде где Более полно св-ва реальных жидкостей и газов учитываются в модели вязкой жидкости. Для вязкой жидкости тензор напряжений определяется не только давлением, но и тензором скорости деформации сплошной среды. Для вязкой жидкости тензор напряжений принимается в форме Для понимания, что представляет из себя вязкая жидкость, определенная зависимостью (8.44), рассмотрим такое течение жидкости, когда скорость частиц параллельна оси ох и зависит только от координаты у. Выберем внутри жидкости 
Сплошная среда, для которой тензор напряжений и тензор деформации связаны линейной зависимостью, называется идеально упругим телом. Само уравнение линейной зависимости называется законам Гука, который для изотропных сред может быть записан в одной из двух форм:
перпендикулярно к двум его торцам в направлении оси ох, то для тензора напряжений и тензора деформаций получим
Так как
Поскольку Рассмотренные здесь модели сплошных сред базируются на значительной идеализации свойств реальных сред. Построение более полных моделей требует привлечения законов термодинамики и выходит за рамки механики.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 501. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
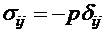 , (8.42)
, (8.42)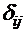 — символ Кронекера. Вследствие (8.42) для плотности поверхностной силы получим
— символ Кронекера. Вследствие (8.42) для плотности поверхностной силы получим  ,
, 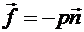 , (8.43) то есть в идеальной жидкости поверхностная сила всегда направлена по нормали к площадке. Ее величина не зависит от ориентации площадки и определяется одной скалярной функцией р, называемой давлением. Давление — положительная величина. В формуле (8.42) выбран знак минус потому, что в реальных сплошных средах, для которых пригодна модель идеальной жидкости, сила давления всегда направлена внутрь выделенного объема сплошной среды противоположно внешней нормали.
, (8.43) то есть в идеальной жидкости поверхностная сила всегда направлена по нормали к площадке. Ее величина не зависит от ориентации площадки и определяется одной скалярной функцией р, называемой давлением. Давление — положительная величина. В формуле (8.42) выбран знак минус потому, что в реальных сплошных средах, для которых пригодна модель идеальной жидкости, сила давления всегда направлена внутрь выделенного объема сплошной среды противоположно внешней нормали.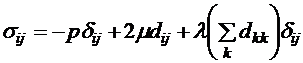 (8.44) где
(8.44) где 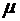 и
и 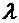 - постоянные коэффициенты, называемые первым и вторым коэффициентами вязкости. Если среда несжимаема, что выполняется для большинства жидкостей, то для нее
- постоянные коэффициенты, называемые первым и вторым коэффициентами вязкости. Если среда несжимаема, что выполняется для большинства жидкостей, то для нее 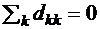 и в выражении (8.44) последнее слагаемое пропадает. Мы ограничимся только случаем несжимаемой вязкой жидкости.
и в выражении (8.44) последнее слагаемое пропадает. Мы ограничимся только случаем несжимаемой вязкой жидкости.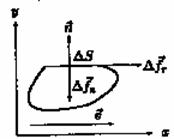 объем, имеющий площадку, нормаль к которой параллельна оси оу (рис. 8.3). Тогда тензор скорости деформаций, тензор напряжений и векторы, изображенные на рис. 8.3, будут иметь следующие компоненты:
объем, имеющий площадку, нормаль к которой параллельна оси оу (рис. 8.3). Тогда тензор скорости деформаций, тензор напряжений и векторы, изображенные на рис. 8.3, будут иметь следующие компоненты: 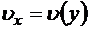 ,
, 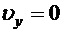 ,
, 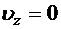 ,
, 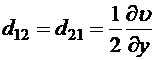 ,
, 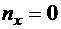 ,
, 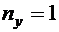 ,
, 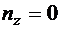 ,
,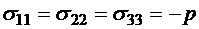 ,
, 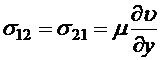 , (8.45)
, (8.45)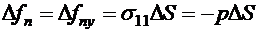 ,
, 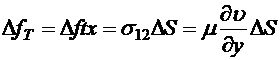 . В вязкой жидкости наряду с силой давления возникает касательная к выделенной площадке сила. Если
. В вязкой жидкости наряду с силой давления возникает касательная к выделенной площадке сила. Если 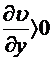 , то верхние слои жидкости увлекают нижние слои с силой, пропорциональной величине этой производной. Коэффициент пропорциональности это коэффициент вязкости
, то верхние слои жидкости увлекают нижние слои с силой, пропорциональной величине этой производной. Коэффициент пропорциональности это коэффициент вязкости 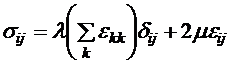 , (8.46)
, (8.46)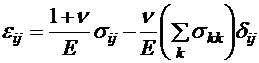 . (8.47) Постоянные
. (8.47) Постоянные 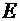 называется модулем Юнга, постоянная
называется модулем Юнга, постоянная 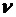 - коэффициентом Пуассона. Для того чтобы найти связь этих двух наборов постоянных, необходимо в уравнениях (8.46) и (8.47) положить
- коэффициентом Пуассона. Для того чтобы найти связь этих двух наборов постоянных, необходимо в уравнениях (8.46) и (8.47) положить 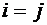 и просуммировать их. В результате получаются формулы:
и просуммировать их. В результате получаются формулы: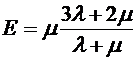 ,
, 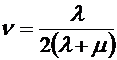 . (8.48) Для уяснения смысла закона Гука, задаваемого формулами (8.46) и (8.47), рассмотрим прямоугольный параллелепипед, ребра которого параллельны коорди
. (8.48) Для уяснения смысла закона Гука, задаваемого формулами (8.46) и (8.47), рассмотрим прямоугольный параллелепипед, ребра которого параллельны коорди 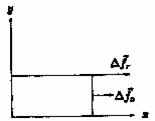 натным осям (рис. 8.4). Если поверхностные силы приложены только
натным осям (рис. 8.4). Если поверхностные силы приложены только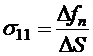 ,
, 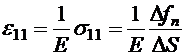 ,
, 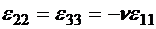 . (8.49)
. (8.49)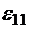 что относительное удлинение образца вдоль оси ох, то формула (8.49) дает известное выражение закона Гука для удлинения образца. Она также показывает, что при удлинении образец будет становиться тоньше. Если же поверхностные напряжения приложены по касательной к торцам, как на рисунке, вдоль оси ох, то получим деформацию сдвига, которая описывается формулами
что относительное удлинение образца вдоль оси ох, то формула (8.49) дает известное выражение закона Гука для удлинения образца. Она также показывает, что при удлинении образец будет становиться тоньше. Если же поверхностные напряжения приложены по касательной к торцам, как на рисунке, вдоль оси ох, то получим деформацию сдвига, которая описывается формулами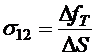 ,
, 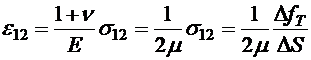 . (8.50)
. (8.50)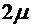 , является коэффициентом пропорциональности между касательными напряжениями и сдвигами сплошной среды, то коэффициент
, является коэффициентом пропорциональности между касательными напряжениями и сдвигами сплошной среды, то коэффициент