
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Фазовое пространство, скобки Пуассона.Для наглядного геометрического изображения решений канонических уравнений (7.6) вводится понятие фазового пространства. Фазовое пространство — это абстрактное пространство 2s измерений, на координатных осях которого откладываются обобщенные координаты и обобщенные импульсы. Система координат в фазовом пространстве считается декартовой системой координат. Решение канонических уравнений дает 2s функций
Канонические уравнения — это система обыкновенных дифференциальных уравнений первого порядка. Поэтому начальные данные для нее задаются только на сами неизвестные функции. Задание и некоторый момент времени t0 начальных данных
В статистической физике вводится понятие статист.ического ансамбля. Статистический ансамбль — это множество идентичных механических систем, для которых заданы различные начальные данные. В фазовом пространстве статистический ансамбль изобрази гея множеством точек, которые можно рассматривать как частицы сплошной среды, называемой фазовой жидкостью. Если в начальный момент времени в фазовой жидкости выделить некоторый объем, го при движении каждой частицы фазовой жидкости по своей фазовой траектории этот объем будет перемещаться и деформироваться. Однако вследствие выполнения канонических уравнений величина этого объема не меняется при его перемещении, то есть фазовая жидкость является несжимаемой жидкостью. Это утверждение носит название теоремы Лиувилля. Теорема Лиувилля применяется для обоснования функции распределения в статистической физике.  Рассмотрим произвольную функцию координат импульсов и времени мени. Так как координаты и импульсы зависят от времени, то производную считаем как производную от сложной функции. В результате получим Производные от координат и импульсов по времени с помощью канонических уравнений (7.6) заменим на производные от функции Гамильтона, Тогда выражение (7.15) приводится к виду
Определим новую величину, называемую скобкой Пуассона функций H и f, согласно формуле (7.17)
Тогда полная производная от функции
(7.18)
Формула (7.18) дает производную по времени от любой функции координат, импульсов и времени. Если в качестве таких функций возьмем обобщенные координаты qi, то получим первую группу канонических уравнений:
Точно так же при подстановке в скобку Пуассона (7.17) вместо функции f обобщенных импульсов pi из (7.18) получается вторая группа канонических уравнений. Таким образом, формула (7.18) включает в себя и канонические уравнения. При построении квантовой механики Гейзенберг использовал обобщение формулы (7.18) для получения производной по времени для операторов, описывающих физические величины в квантовой механике. Если некоторая функция координат и импульсов не зависит явно от времени и ее скобка Пуассона с функцией Гамильтона Н равна нулю, то эта функция остается постоянной при движении механической системы, и, следовательно, имеется закон сохранения. Например, скобка Пуассона функции Гамильтона с функцией Гамильтона тождественно равна нулю. Поэтому если функция Гамильтона не зависит явно от времени, то она остается постоянной. Поскольку функция Гамильтона равна энергии механической системы, то это означает, что выполняется закон сохранения механической энергии.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 733. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 В каждый момент времени эти функции определяют в фазовом пространстве одну точку. Эта точка называется изображающей точкой, и полностью определяет состояние механической системы. С течением времени значения функций
В каждый момент времени эти функции определяют в фазовом пространстве одну точку. Эта точка называется изображающей точкой, и полностью определяет состояние механической системы. С течением времени значения функций 
 изменяются и изображающая точка перемещается по фазовому пространству, описывая кривую, которая называется фазовой траекторией. Движение механической системы с любым конечным числом степеней свободы всегда изображается в фазовом пространстве как траектория изображающей точки. От размерности механической системы зависит только размерность фазового пространства.
изменяются и изображающая точка перемещается по фазовому пространству, описывая кривую, которая называется фазовой траекторией. Движение механической системы с любым конечным числом степеней свободы всегда изображается в фазовом пространстве как траектория изображающей точки. От размерности механической системы зависит только размерность фазового пространства.
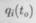 означает задание точки в фазовом пространстве. Поскольку начальные данные полностью определяют частное решение канонических уравнений, то из каждой точки фазового пространства выходит только одна фазовая траектория. Поэтому фазовые траектории не пересекаются.
означает задание точки в фазовом пространстве. Поскольку начальные данные полностью определяют частное решение канонических уравнений, то из каждой точки фазового пространства выходит только одна фазовая траектория. Поэтому фазовые траектории не пересекаются. и найдем от нее полную производную по вре-
и найдем от нее полную производную по вре- (7.15)
(7.15) (7.16)
(7.16) запишется в виде
запишется в виде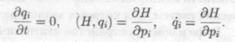 (7.19)
(7.19)