
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод Эйлера описания сплошной среды.Механика сплошной среды изучает движение газообразных, жидких и твердых деформируемых тел. При этом не учитывается молекулярное строение вещества, а предполагается его непрерывное распределение. В сплошной среде можно выделить малый объем
Частная производная при  По известной зависимости При описании сплошной среды по методу Эйлера для вычисления полных производных по времени для отдельных частиц сплошной среды следует радиус-вектор
По тому же правилу вычисляется поле ускорений сплошной среды:
27. Производная по подвижному объему, ур-ние неразрывности. (Дифференциальные и интегральные соотношения, подвижный объем). В механике сплошной среды многие величины задаются своими плотностями. Например, плотность массы, плотность импульса и плотность момента импульса определяются по формулам:
Тогда те же величины для конечного объема сплошной среды получаются интегрированием по объему: Уравнения механики сплошной среды также могут быть записаны в дифференциальной и интегральной формах. Объем, по которому ведется интегрирование, может быть фиксированным или подвижным. Под подвижным объемом в механике сплошной среды понимают объем, который движется вместе со сплошной средой. Поэтому частицы сплошной среды не пересекают поверхность, ограничивающую подвижный объем.
Если некоторая величина А задана объемной плотностью
Разделив соотношение (8.7) на
Поверхностный интеграл в формуле (8.8) с помощью теоремы Остроградского—Гаусса можно преобразовать в объемный:
Подстановка этого объемного интеграла в равенство (8.8) приводит к следующим выражениям для производной по подвижному объему:
Переход от одной формы к другой осуществляется при помощи соотношения
Если Положим в формуле (8.10) А = т. Так как частицы сплошной среды не пересекают границ подвижного объема, то т=const и производная от массы =0. Поэтому нулю должны быть равны подынтегральные выражения в (8.10), что даст уравнения Уравнения (8.12) называются уравнениями неразрывности и выражают собой закон сохранения массы. Такие же уравнения выполняются для любой физической величины (например, заряда), которая остается постоянной внутри подвижного объема. Найдем сейчас производную по времени от импульса сплошной среды, заключенной в подвижном объеме. Из определения импульса (8.5) и выражения (8.10) для производной имеем
Сумма во внутренних скобках под знаком интеграла (8.13) обращается в нуль вследствие уравнения неразрывности (8.12). В результате получаем
Аналогичным образом можно показать, что производная от момента импульса конечного объема сплошной среды вычисляется по формуле
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 571. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
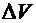 , имеющий массу
, имеющий массу 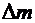 , и устремить
, и устремить 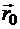 . В любой другой момент времени положение этих частиц будет задаваться радиусом-вектором
. В любой другой момент времени положение этих частиц будет задаваться радиусом-вектором 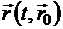 . Здесь координаты x0, y0, z0 радиуса-вектора
. Здесь координаты x0, y0, z0 радиуса-вектора 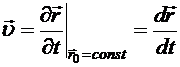 ,
, 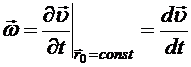 . (8.1)
. (8.1)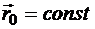 в механике сплошных сред называется полной производной и обозначается как полная производная. Метод описания сплошной среды, когда все характеристики сплошной среды отслеживаются из начальной конфигурации, называется методом Лагранжа.
в механике сплошных сред называется полной производной и обозначается как полная производная. Метод описания сплошной среды, когда все характеристики сплошной среды отслеживаются из начальной конфигурации, называется методом Лагранжа.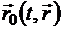 . Подстановка зависимости
. Подстановка зависимости 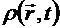 , то вычисление полной производной по времени от нее даст
, то вычисление полной производной по времени от нее даст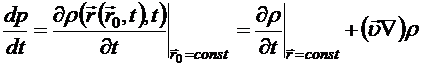 , (8.2)
, (8.2) .
. . (8.3)
. (8.3) ,
, 
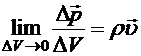 ,
, 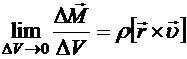 . (8.4)
. (8.4)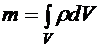 ,
, 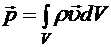 ,
, 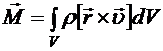 . (8.5)
. (8.5)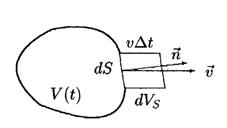 Рис. 8.1 При вычислении производных по времени по подвижному объему необходимо учитывать, что с течением времени подвижный объем может измениться. Как видно из рис. 8.1, за время
Рис. 8.1 При вычислении производных по времени по подвижному объему необходимо учитывать, что с течением времени подвижный объем может измениться. Как видно из рис. 8.1, за время 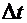 площадка
площадка 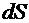 поверхности, ограничивающей объем, сместится на расстояние
поверхности, ограничивающей объем, сместится на расстояние 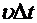 . За счет этого смещения объем увеличится на
. За счет этого смещения объем увеличится на 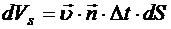 . Все изменение объема получается интегрированием этого увеличения по замкнутой поверхности, ограничивающей подвижный объем:
. Все изменение объема получается интегрированием этого увеличения по замкнутой поверхности, ограничивающей подвижный объем: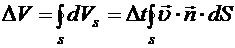 . (8.6)
. (8.6) и вычислена интегрированием по подвижному объему
и вычислена интегрированием по подвижному объему 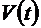 , то ее приращение за время
, то ее приращение за время 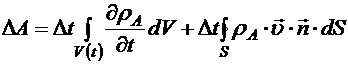 . (8.7)
. (8.7)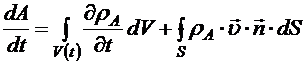 . (8.8)
. (8.8)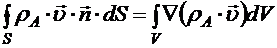 . (8.9)
. (8.9)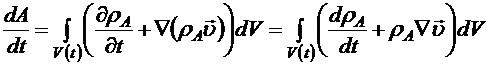 . (8.10)
. (8.10)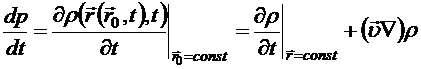 (8.2). Если положить
(8.2). Если положить 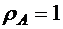 , то величина А равна подвижному объему и формула (8.10) дает производную от подвижного объема, которая равна
, то величина А равна подвижному объему и формула (8.10) дает производную от подвижного объема, которая равна 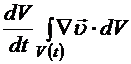 . (8.11)
. (8.11)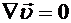 , то величина подвижного объема остается постоянной при движении сплошной среды. Такая сплошная среда называется несжимаемой средой.
, то величина подвижного объема остается постоянной при движении сплошной среды. Такая сплошная среда называется несжимаемой средой.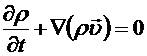 ,
, 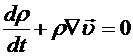 . (8.12)
. (8.12)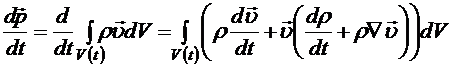 . (8.13)
. (8.13)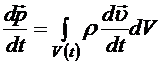 . (8.14)
. (8.14)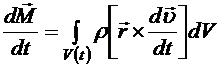 . (8.15)
. (8.15)