Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Реализация математических моделей на ЭВМ.Решение оптимизационной задачи линейного программирования в Excel Пусть предприятие (например, мебельная фабрика) производит столы и стулья. Расход ресурсов на их производство и прибыль от их реализации представлены в табл. Данные о расходе ресурсов и прибыли от реализации продукции
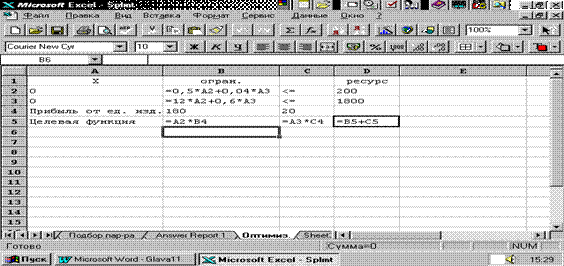
Кроме того, на производство 80 столов заключен контракт с муниципалитетом, который, безусловно, должен быть выполнен. Необходимо найти такую оптимальную производственную программу, чтобы прибыль от реализации продукции была максимальной. Пусть x 1 количество столов, х 2 количество стульев. Тогда система ограничений и целевая функция запишутся следующим образом: 180 x 1 + 20 х 2 ®max (целевая функция); 0,5 x 1 + 0,04 х 2 12 x 1 + 0,6 х 2 x 1 x 1 x 1 , х 2 целые числа. Для решения задачи в Excel запишем ее в виде, представленном на рис. 5.4. Для решения задачи вызовем меню СервисПоиск решения ( ToolsSolver ). В открывшемся диалоговом окне Поиск решения (рис. 5.5) укажем: · адрес целевой ячейки (в нашем примере D5); · диапазон искомых ячеек (А2:A3); · ограничения: А2 >= 80, A2:A3 = целое, A2:A3 >= 0, В2 <= D2, B3 <= D3.
Рис. 5.4. Запись исходных данных для решения задачи
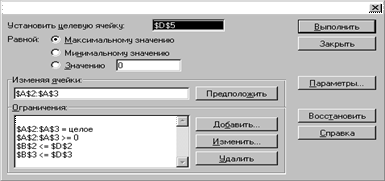
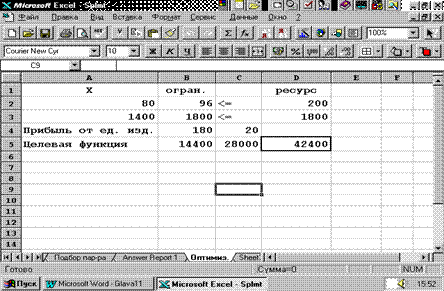
Рис. 5.5. Диалоговое окно Поиск решения Добавления, изменения и удаления ограничений производятся с помощью кнопок Добавить, Изменить, Удалить ( Add, Change, Delete ) .  Для нахождения оптимального решения нажмем кнопку Выполнить ( Solve ). В результате в таблице получим значение целевой функции 42400 млн руб. при x 1 = 80 и x 2 = 1400 (рис. 5.6).
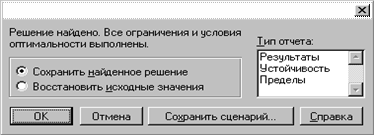
Рис. 5.6. Рабочий лист с найденным оптимальным решением Диалоговое окно Результаты поиска решения позволяет (рис. 5.7): · сохранить на текущем рабочем листе найденное оптимальное решение; · восстановить первоначальные значения; · сохранить сценарий; · выдать отчеты по результатам, устойчивости, пределам, необходимые для анализа найденного решения. Если щелкнуть по кнопке ОК, то на месте исходной таблицы получим таблицу с найденными оптимальными значениями (см. рис. 5.6).
Рис. 5.7. Диалоговое окно Результаты поиска решения Как видно из результатов решения, предприятию производить столы не очень выгодно. Поэтому оно ограничило объем их выпуска в количестве, необходимом для выполнения контракта. Остальные ресурсы направлены на производство стульев.
Общие модели развития экономики. Общие модели экономики представляются производственными функциями. Производственные функции – количественное соотношение, описывающее технологическую зависимость между затратами производственных факторов и результатами деятельности производственного объекта. Макроэкономическую функцию впервые на уровне страны использовали Кобб и Дуглас. y=A*K^α*L^β (статистическая функция Кобба-Дугласа), где К – капитал, L – труд, A,α,β – коэффициенты, причем α+β=1.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 335. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
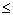 200 (ограничения по древесине);
200 (ограничения по древесине);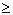 80 (контракт с муниципалитетом);
80 (контракт с муниципалитетом);