
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Регулярные методы минимизации функций (прямые методы и методы сопряженных направлений).Конспект: Прямые методы (при работе не используются производные от целевой функции) Методы сопряженных направлений (тоже не используются производные от целевой функции)
К прямым относят симплексные методы (Нелдера-Мида)
Википедия: Метод Нелдера —Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной(точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям. Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума. Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс. Более развитый подход к исключению локальных экстремумов предлагается в алгоритмах, основанных на методе Монте-Карло, а также в эволюционных алгоритмах. Липа какая-то: Метод сопряженных направлений Пауэлла Описание алгоритма: Метод ориентирован на решение задач с квадратичными целевыми функциями. Основная идея алгоритма заключается в том, что если квадратичная функция:
приводится к виду сумма полных квадратов
то процедура нахождения оптимального решения сводится к В методе Пауэлла поиск реализуется в виде:
вдоль направлений Сопряженные направления определяются алгоритмически. Для нахождения экстремума квадратичной функции  Алгоритм метода: Шаг 1. Задать исходные точки Шаг 2. Произвести одномерный поиск из точки Шаг 3. Произвести одномерный поиск из точки Шаг 4. Вычислить направление Шаг 5. Провести одномерный поиск из точки
Методы минимизации функций (случайный поиск). Применяются численные методы поиска экстремума функции. Эти методы делятся на 2 группы: 1. методы случайного поиска минимума ф-ции 2. регулярные методы
методы случайного поиска
Методы случайного поиска бывают без обучения и с самообучением. В методах без обучения величина и направление случайного вектора Методы с самообучением. При работе используется информация об оптимальных значениях параметров на предыдущих шагах поиска. Недостаток – точность недостаточная для решения практических задач. 1. метод покоординатного обучения 2. метод повторяющегося случайного поиска 3. метод случайного поиска с постоянным радиусом 4. метод переменного поиска с переменным радиусом
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 699. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 <= что это за рисунок и какому методу – без понятия.
<= что это за рисунок и какому методу – без понятия.


 одномерным поискам по преобразованным координатным направлениям.
одномерным поискам по преобразованным координатным направлениям.
 ,
,  , называемых
, называемых  -сопряженными при линейной независимости этих направлений.
-сопряженными при линейной независимости этих направлений.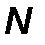 переменных необходимо выполнить
переменных необходимо выполнить  одномерных поисков.
одномерных поисков. ,
, 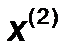 и направление
и направление  . В частности, направление
. В частности, направление 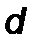 может совпадать с направлением координатной оси;
может совпадать с направлением координатной оси; в направлении
в направлении  получить точку
получить точку  , являющуюся точкой экстремума на заданном направлении;
, являющуюся точкой экстремума на заданном направлении; в направлении
в направлении  получить точку
получить точку  ;
; ;
; (либо
(либо  ) в направлении
) в направлении  с выводом в точку
с выводом в точку  .
.
 не зависят от номера шага поиска. Недостаток – медленная работа, по мере работы метода ухудшается точность.
не зависят от номера шага поиска. Недостаток – медленная работа, по мере работы метода ухудшается точность.