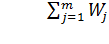Задачи оптимизации проектных решений. Понятие целевой функции.

Оптимизацией параметров работы авто и его систем имеет важное значение в процессе проектирования. Степень соответствия расчетного параметра заданному определяется скалярный метод ошибки. Оптимальным считается такое значение проектируемого параметра, которое соответствует min целевой функции.

Среди задач оптимизации выделяют задачи 2 классов:

1.Задачи безусловной оптимизации

2.Задачи условной оптимизации

1. Ф(Х*)=minФ(Х)

Х* - оптимальное значение параметра

2. Ф(Х*)=min Ф(Х)

А(X,Y)=0 B(X,Y)=0

При оптимизации параметров с использованием нескольких критериев появляется понятие частной целевой функции

Фj(X) j=1,…m

Ф(Х)=

Во многих методах решение задач безусловной оптимизации используется понятие штрафов

Ф(Х*)=minФ(Х)+Фштр(Х)

Функция штрафов позволяет контролировать ограничения, которые возникают при применении расчетной функции.

Этапы работы программы метода конечных элементов. Фаза постпроцессорной обработки.

Этапы работы программы конечных элементов: 3 Этапа

1.Препроц. Обработка

2.Анализ модели ( расч. На Пк в программе)

3.Оценка и анализ результатов.

Препроц. Обработка

Геометр.парам  характер. Нагрузок граничные условия  свойства материала

вывод.перем.         Вывод. Велич.  Графич.вывод.  вывод границ. Световая    аним.проц.

узлов.                        Нагрузок            перемещ.            Напряж.          Диференц. Нагруж.

Регулярные методы минимализации функции (градиентные и сопряженных градиентов)

Регулярные методы виды:

-Прямые – при работе не исп. Произв. От целевых функций.

-Сопряж.направл.-не исп. Произв. От цел.функций.

-Градиентные-при работе исп.первые произв. По целев. Функции.

-Квази-Ньютоновские

-Быстросход.-исп. Более высокие 2-ые произв. От целев. Функции.

Прямые методы

    -симплексные

    -Нелдера-Мида

Ф(Х₃)› Ф(Х₂)› Ф(Х₁)

Ф(Х₄)‹ Ф(Х₃)

Методы градиентные

1.Метод наискорейшего спуска. Формула метода.

         X_к+1=х_к-λ_к*𝛛ɸ(х_к)/𝛛_к

λ_к-скалярный коэффициент определяющий длину шага поиска вдоль напр. Напр.задается методом антиградиента.

        𝛛ɸ/𝛛х₁

∆ɸ=     𝛛ɸ/𝛛х_i

                𝛛ɸ/𝛛х_n

Λ_к- нах. Путем минимизации функции

Min ɸ(x_k-λ_k*𝛛ɸ(x_k)/𝛛x_k)

λ_e(0,∞)

        2. Метод сопряженных градиентов. Идея состоит в поиске минимума функции ɸ_(к) вдоль напр. S_k –опред.линией комб. Текущего напр.поиска и предыдущ. Напр. Поиска метод обл.сверхлинейной сходимостью.

Ιx_k+1-x_cΙ‹c_kΙx_k-x_k-1Ι

C_k →0 k→∞

Общая формула метода

Х_к+1=k_k+λ_kS_k

Вектор S_k опред. Черех произв. От функции ⱷ_к

S_k=F(ɸ’(x₀)….., ɸ’(x_k))

Ньютоновские методы минимализации функции

Метод Ньютона-это методы второго порядка.

X_k+1= x_k-{ɸ’’(x_k)}^-1

Метод Ньютона , имеет очень узкую область сходимости, если их оптим. лежит ближе к Х₀.

Недостатки метода Ньютона, частично устр. В модиф. Методе Ньютона.

X_k+1=x_k-λ_к{ɸ’’(x_k)}^-1ɸ’(x_k)                λ_к{ɸ’’(x_k)}^-1 -это обратная матрица Гессе

λ_k=min{ɸ(x_k-λ_k(ɸ’’(х_к))^-1ɸ’(x_k)}

В обратной матрице 2-ая производная не должна равняться -0.

Квази-Ньютоновские методы.

X_k+1 = x_k-λ_кƞ_кφ'(x_k)