
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оценка статистической совокупностиАнализ исходной информации начинается с проверки статистической совокупности относительно однородности распределения и наличия аномальных наблюдений. Для оценки статистической совокупности рассчитываются следующие показатели: 1) Средний объем закупок в квартал(
где В нашем примере:
2) Среднее квадратичное отклонение (
Исходя из показателя среднего квадратичного отклонения можно сделать вывод о наличии аномальных наблюдений в совокупности. Для этого используется правило «3 сигма», согласно которому аномальными считаются те наблюдения, которые не входят в интервал
В данном примере искомый интервал имеет значения:
Так как наименьшее значение показателя больше, чем верхняя граница интервала (33,927т > 29,384 m), а наибольшее значение – меньше, чем нижняя граница (49,783т < 59,912 m), можно сделать вывод, что аномальных значений показателя не наблюдается, и совокупность будет рассматриваться в исходном объеме. 3) Коэффициент вариации (V):
Если значение коэффициента вариации меньше, чем 33,3 %, то совокупность признается однородной и ее исследование продолжается. 
Таким образом, совокупность однородна и ее дальнейшее исследование имеет смысл.
Анализ основной тенденции развития Оценка основной тенденции развития может проводиться по разным корреляционно-регрессионным динамическим зависимостям. Однако, чаще всего используют линейную связь, которая имеет вид:
где Для определения параметров линейного уравнения прогноза используются следующие формулы:
Для выявления основной тенденции развития и построения тренда используем метод отсчета от условного нуля. Необходимые исходные данные и промежуточные расчеты приведены в таблице 1.2.
Таблица 1.2. Расчет параметров линейного уравнения прогноза
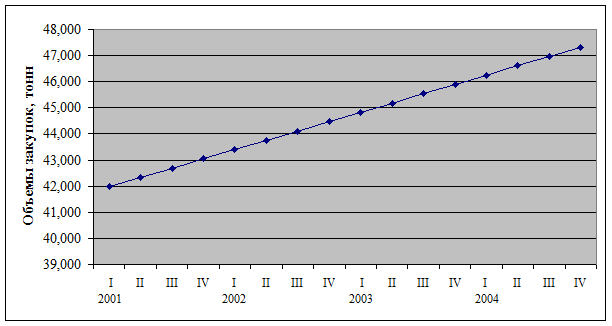
На рисунке 1.2. изображена основная тенденция (тренд) изменения объемов закупок за четыре года.
Рис. 1.2. Тренд объемов закупок продовольственных товаров длительного хранения за 2001–2004 годы Используя формулы (1.6–1.7) и необходимые значения, рассчитанные в таблице 1.2. получаем следующие значения параметров уравнения прогноза:
Уравнение прогноза закупок имеет вид:
Для оценки качества прогноза рассчитываются следующие показатели: 1) абсолютная ошибка прогноза:
2) относительная ошибка прогноза:
Так как относительная ошибка прогноза меньше 25 %, можно сделать вывод, что модель достаточно хорошо отображает происходящие изменения. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 397. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
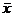 ):
):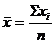 (1.1)
(1.1)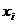 – значение объема закупок в
– значение объема закупок в 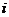 -й квартал, т; п – количество рассматриваемых кварталов.
-й квартал, т; п – количество рассматриваемых кварталов.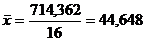 т.
т.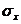 ):
):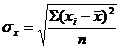 ; (1.2)
; (1.2)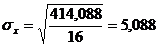 т.
т.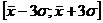 . (1.3)
. (1.3)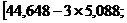
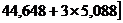 =
=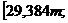
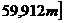 .
.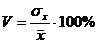 (1.4)
(1.4)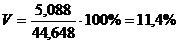 .
.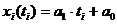 ; (1.5)
; (1.5)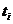 – порядковый номер периода;
– порядковый номер периода; 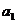 ,
, 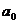 – расчетные параметры уравнения прогноза.
– расчетные параметры уравнения прогноза.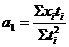 ;
; 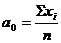 . (1.6–1.7)
. (1.6–1.7)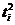
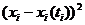
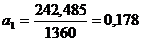 ;
; 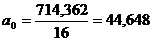 т.
т.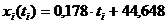 .
.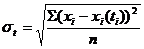 ; (1.8)
; (1.8)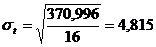 т.
т.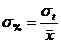 ; (1.9)
; (1.9)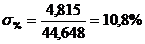 .
.