
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Координатный способ задания движения точкиСтр 1 из 13Следующая ⇒ Министерство образования и науки российской федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА (КИНЕМАТИКА)
КОНСПЕКТ ЛЕКЦИЙ И СОДЕРЖАНИЕ
Направление подготовки 270800 – Строительство_______
Профиль подготовки ______________________________ Квалификация (степень) выпускника бакалавр_______________________ Форма обучения очная ________________________
Составитель: проф. В.И.Антонов
г. Москва 2012г.
ЛЕКЦИЯ 1 (5) Кинематика – один из разделов курса теоретической механики, в котором рассматривается движение тел без учета причин, приводящих к изменению этого движения, т.е. без учета сил. Под движением в механике понимаем изменение с течением времени положения тела в пространстве по отношению к другим телам. Это означает, что изучая движение какого–либо тела, необходимо указать другое тело — тело отсчета, по отношению к которому рассматривается движение. С телом отсчета жестко связана система координат. Тело отсчета, связанная с ним система координат и счетчик времени — часы образуют систему отсчета. Поскольку в классической механике считается, что время не зависит от движения тел и одинаково во всех точках пространства и во всех системах отсчета, то, говоря о системе отсчета, обычно задают только тело отсчета, а еще чаще, только систему координатных осей, связанных с телом отсчета.  Положение точки или тела по отношению к выбранной системе отсчета определяется некоторыми параметрами — координатами. Движение будет задано, если известен закон, по которому эти координаты изменяются с течением времени. Разработка методов, при помощи которых может быть задано движение точки или тела — одна из задач кинематики. Другая задача кинематики состоит в том, чтобы зная закон движения точки или тела, определить кинематические величины, характеризующие движение (скорости, ускорения и т.д.). Движение точки по отношению к выбранной системе отсчета считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени. КИНЕМАТИКА ТОЧКИ Координатный способ задания движения точки Положение точки
координат, в которой законы движения точки имеют вид:
где Вектор
где
Непрерывная кривая, которую описывает точка при своем движении, называется траекторией точки.
Уравнения (1.1) представляют собой уравнения траектории в параметрической форме, где роль параметра играет время Намного удобнее получить уравнение траектории в координатной форме. Для этого необходимо из уравнений движения (1.1) исключить параметр
Пример
Даны законы движения точки в координатной форме:
Определить траекторию точки.
Исключая время из уравнений движения, получаем уравнение параболы:
Однако, уравнения движения и заданный интервал времени налагают ограничения на область допустимых значений координат:
при
Таким образом, траекторией будет только правая ветвь параболы (Рис. 1.2).
Скорость точки Быстроту движения точки характеризует ее скорость, к определению которой мы сейчас переходим. Пусть в момент времени (Рис. 1.3). Вектор
Понятно, что средняя скорость зависит от выбранного промежутка времени и тем точнее характеризует быстроту движения, чем меньшим выбран промежуток времени Скоростью точки в данный момент времени называется предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при величине промежутка времени, стремящейся к нулю:
Таким образом,
вектор скорости равен первой производной по времени от радиуса-вектора точки.
В пределе при
вектор скорости направлен по касательной к траектории, причем в сторону движения точки.
Пусть движение точки задано в координатной форме, т.е. уравнениями (1.1). Используя равенство (1.2) и учитывая, что орты координатных осей со временем не изменяются, получаем:
Таким образом, проекции вектора скорости на оси координат равны первым производным по времени от соответствующих координат точки:
Ускорение точки Быстроту изменения вектора скорости характеризует ускорение точки. Пусть в момент времени Ускорением точки называется предел отношения приращения вектора скорости к промежутку времени, за который это приращение произошло, при величине промежутка времени, стремящейся к нулю:
Таким образом, ускорение точки равно первой производной по времени от вектора скорости точки или второй производной по времени от радиуса-вектора точки.
Если траектория – плоская кривая, то вектор ускорения лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория – пространственная кривая, то при предельном переходе
вектор ускорения точки лежит в соприкасающейся к траектории в данной точке плоскости, причем направлен в сторону вогнутости траектории.
Пусть движение точки задано в координатной форме, т.е. уравнениями (1.1). Тогда
Таким образом, проекции вектора ускорения на координатные оси равны первым производным по времени от соответствующих проекций вектора скорости или, учитывая равенства (5.4), вторым производным по времени от соответствующих координат точки:
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
ЛЕКЦИЯ 2 (6)
|
|||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 256. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 в системе отсчета полностью определяется ее координатами. Если известна зависимость координат от времени, движение точки считается заданным. В зависимости от содержания решаемой задачи можно использовать любую систему координат (декартову, цилиндрическую, сферическую и т.д.), наиболее целесообразную для решения данной задачи. Мы, в основном, будем использовать прямоугольную декартову систему
в системе отсчета полностью определяется ее координатами. Если известна зависимость координат от времени, движение точки считается заданным. В зависимости от содержания решаемой задачи можно использовать любую систему координат (декартову, цилиндрическую, сферическую и т.д.), наиболее целесообразную для решения данной задачи. Мы, в основном, будем использовать прямоугольную декартову систему
 (1.1)
(1.1)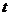 – время.
– время.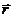 , проведенный из начала координат в точку
, проведенный из начала координат в точку  (1.2)
(1.2)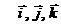 – единичные векторы (орты) координатных осей.
– единичные векторы (орты) координатных осей.

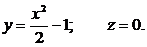
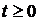 имеем:
имеем: 
 переходит в положение
переходит в положение  , радиус–вектор которого
, радиус–вектор которого 
 называется вектором перемещения точки за время
называется вектором перемещения точки за время  . Если разделить вектор перемещения на
. Если разделить вектор перемещения на 
 (1.3)
(1.3)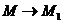 секущая
секущая  , по которой направлена средняя скорость, занимает положение касательной к траектории в точке
, по которой направлена средняя скорость, занимает положение касательной к траектории в точке 
 (1.4)
(1.4) , а в момент
, а в момент  (Рис. 1.4).
(Рис. 1.4).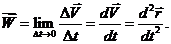 (1.5)
(1.5)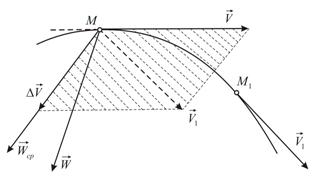
 плоскость, содержащая вектор среднего ускорения (на чертеже заштрихована), будет поворачиваться вокруг вектора
плоскость, содержащая вектор среднего ускорения (на чертеже заштрихована), будет поворачиваться вокруг вектора 
 (1.6)
(1.6)