
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Движение точки под действием восстанавливающей силы
Пусть на точку действует только восстанавливающая сила. Полагая в уравнении (2.5)
Здесь и в дальнейшем полагаем Уравнение (2.8) представляет собой обыкновенное линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общее решение уравнения (2.8) имеет вид:
где Дифференцируя решение (2.9) по времени, получаем закон изменения скорости точки:
Для определения постоянных интегрирования
при в уравнения (10.9) и (10.10). Получаем:
или
Скорость точки при этом вычисляется по формуле: 
Движение, совершаемое точкой под действием восстанавливающей силы, называется простым гармоническим или свободным незатухающим колебанием (Рис.2.2). Постоянная Как видно, движение будет периодическим. Периодом колебаний называется промежуток времени Величина
Влияние постоянной силы на свободные незатухающие колебания
Пусть кроме восстанавливающей силы (2.1) на точку действует постоянная по модулю и направлению сила, например, сила тяжести. Для наглядности рассмотрим колебания груза, прикрепленного к концу пружины (Рис.2.3). На груз действуют две силы: сила тяжести и реакция пружины, величина которой пропорциональна удлинению пружины:
Выберем начало отсчета в положении статического равновесия
Учитывая условие статического равновесия:
Таким образом, наличие постоянной силы не изменяет характера движения – оно остается простым гармоническим колебанием. Действие постоянной силы приводит только к тому, что центр колебаний смещается в сторону действия постоянной силы.
|
|||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 411. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и 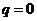 , получаем:
, получаем: (2.8)
(2.8) , имея ввиду, что в учебной литературе обычно рассматривается случай прямолинейного движения, хотя все полученные результаты справедливы для движения точки по любой криволинейной траектории.
, имея ввиду, что в учебной литературе обычно рассматривается случай прямолинейного движения, хотя все полученные результаты справедливы для движения точки по любой криволинейной траектории. (2.9)
(2.9) и
и  — постоянные интегрирования.
— постоянные интегрирования.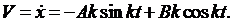 (2.10)
(2.10) (2.11)
(2.11)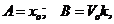 так что общее решение уравнения (10.8) принимает вид:
так что общее решение уравнения (10.8) принимает вид: (2.12)
(2.12)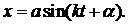 (2.13)
(2.13)
 (2.14)
(2.14) определяет наибольшее отклонение точки от положения равновесия; ее называют амплитудой колебаний. Величина
определяет наибольшее отклонение точки от положения равновесия; ее называют амплитудой колебаний. Величина  , определяющая положение и скорость точки в данный момент времени, называется фазой колебаний;
, определяющая положение и скорость точки в данный момент времени, называется фазой колебаний;  – начальная фаза.
– начальная фаза. , в течение которого точка совершает одно полное колебание
, в течение которого точка совершает одно полное колебание (2.15)
(2.15) , пропорциональная
, пропорциональная  , называется круговой или циклической частотой колебаний.
, называется круговой или циклической частотой колебаний. .
.
 ; ось
; ось  направим вертикально вниз. Тогда
направим вертикально вниз. Тогда  . Дифференциальное уравнение движения точки принимает вид:
. Дифференциальное уравнение движения точки принимает вид:  (2.16)
(2.16) приводим уравнение (2.16) к виду:
приводим уравнение (2.16) к виду: