
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальное уравнение относительного движения точки
Всякое движение точки (или тела) рассматривается по отношению к определенной системе отсчета. До сих пор мы рассматривали движение материальной точки по отношению к так называемой инерциальной системе отсчета, по отношению к которой материальная точка при отсутствии сил может оставаться в покое или движется равномерно и прямолинейно. Инерциальную систему отсчета считают условно неподвижной, а движение
по отношению к ней называют абсолютным. Однако, во многих случаях возникает необходимость рассматривать движение точки или тела по отношению к системе отсчета, которая также движется по отношению к инерциальной системе отсчета. В таком случае говорят об относительном движении точки (или тела). Основное уравнение динамики материальной точки (второй закон Ньютона) справедливо только по отношению к инерциальной системе отсчета. Возникает необходимость составить дифференциальное уравнение движения материальной точки по отношению к неинерциальной системе отсчета. Рассмотрим материальную точку В инерциальной системе отсчета справедлив второй закон Ньютона:

В соответствии с теоремой Кориолиса абсолютное ускорение точки складывается из ускорения относительного
где
Обозначая получаем: Величины Пусть подвижная система отсчета движется по отношению к инерциальной системе поступательно равномерно и прямолинейно. При поступательном движении угловая скорость равна нулю и все точки подвижного пространства движутся одинаково. Ускорение Кориолиса и, следовательно, кориолисова сила инерции обращаются в нуль. Поскольку, кроме того, движение прямолинейное и равномерное, то и переносное ускорение, а следовательно, и переносная сила инерции также обращаются в нуль. В таком случае уравнение относительного движения (1.10) совпадает с уравнением абсолютного движения (1.6) и, следовательно, подвижная система отсчета также будет инерциальной. Таким образом, если существует хотя бы одна инерциальная система отсчета, то их существует бесчисленное множество. Все они движутся друг относительно друга поступательно равномерно и прямолинейно. Из этого результата в свою очередь вытекает, что
никаким механическим экспериментом нельзя установить, находится данная система отсчета в покое или движется поступательно равномерно и прямолинейно.
Сформулированное утверждение составляет содержание принципа относительности Галилея–Ньютона.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
ЛЕКЦИЯ 2 (10) |
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 437. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 с массой
с массой  , на которую действует сила
, на которую действует сила  , являющаяся результатом механического взаимодействия точки с другими материальными телами. Другими словами, сила
, являющаяся результатом механического взаимодействия точки с другими материальными телами. Другими словами, сила  , произвольно перемещающейся по отношению к инерциальной системе отсчета
, произвольно перемещающейся по отношению к инерциальной системе отсчета  (Рис. 1.1).
(Рис. 1.1). (1.6)
(1.6) , ускорения переносного
, ускорения переносного 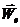 и ускорения Кориолиса
и ускорения Кориолиса  :
:  причем,
причем,  (1.7)
(1.7) – вектор угловой скорости подвижной системы отсчета. Подставляя (1.7) в (1.6), получаем:
– вектор угловой скорости подвижной системы отсчета. Подставляя (1.7) в (1.6), получаем: или
или  (1.8)
(1.8) (1.9)
(1.9)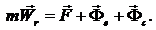 (1.10)
(1.10) и
и  , имеющие размерность силы, называются соответственно переносной и кориолисовой силами инерции. Уравнение (1.10) называется уравнением относительного движения материальной точки. Как видно, уравнение относительного движения составляется так же, как уравнение абсолютного движения, но к действующим на точку силам необходимо добавить переносную и кориолисову силы инерции.
, имеющие размерность силы, называются соответственно переносной и кориолисовой силами инерции. Уравнение (1.10) называется уравнением относительного движения материальной точки. Как видно, уравнение относительного движения составляется так же, как уравнение абсолютного движения, но к действующим на точку силам необходимо добавить переносную и кориолисову силы инерции.