
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ⇐ ПредыдущаяСтр 7 из 7 В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ
Рассмотрим движение материальной точки. Пусть на нее действуют силы На основании аксиомы Д4 имеем Учитывая (4) Если перейти к проекциям, то получим систему дифференциальных уравнений второго порядка, описывающих поведение материальной точки вдоль каждой из осей координат
УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ В ЕСТЕСТВЕННОЙ СИСТЕМЕ КООРДИНАТ
Если уравнение (10) разложить по осям естественной системы координат, получим Учитывая особенности разложения вектора ускорений в естественной системе координат (формулы 4), получим Отметим, что чисто технически решать систему уравнений (14) в два раза проще, чем уравнения (11), потому что только первое из уравнений (14) является дифференциальным второго порядка, второе имеет только первый порядок, а третье вообще не дифференциальное. Однако пользоваться уравнениями (14) можно только в том случае, если заранее известна траектория движения.
ПРИНЦИП Д’АЛАМБЕРА СИЛА ИНЕРЦИИ МАТЕРИАЛЬНОЙ ТОЧКИ – это условная сила, направление действия которой противоположно действительному ускорению точки и которая равна по величине произведению массы точки на её ускорение 
ПРИНЦИП Д’АЛАМБЕРА. Если к заданным внешним силам, действующим в системе, добавить силы инерции тел и их инерционные моменты, то можно считать, что система находится в равновесии. Доказательство. Без доказательства.
СПИСОК ТЕРМИНОВ После тире указан номер страницы, на которой дано определение термина.
Абсолютно твердое (жесткое) тело – 3 Балка - 4 Бинормаль - 18 Векторный закон движения – 16 Вращательное движение - 22 Главный вектор - 8 Главный момент - 8 Гладкая поверхность - 4 Движение инерционное - 25 Движение одномерное - 26 Динамика - 25 Естественная система координат – 18 Естественный закон движения - 18 Заделка - 5 Закон вращательного движения – 23 Инертность - 25 Инерционная система отчета – 25 Инерционный момент - 36 Касательная - 18 Кинематика - 15 Линия действия - 3 Масса материальной точки – 25 Масса тела - 29 Механическая система - 29 Момент инерции материальной точки – 32 Момент инерции тела - 32 Момент пары сил - 7 Момент силы относительно точки – 6 Неподвижный шарнир - 5 Нить - 4 Нормаль - 18 Обратная задача динамики - 25 Ось вращения - 22 Относительное движение - 24 Пара сил - 7 Переносное движение - 24 Плечо - 6 Подвижный шарнир - 5 Порядок решения задач статики – 14 Поступательное движение - 21 Принцип д'Аламбера - 36 Прямая задача динамики – 25 Равнодействующая - 9 Равнозамедленное движение – 21 Равномерное движение – 20 Равнопеременное движение –21 Равноускоренное движение – 21 Радиус инерции - 34 Радиус-вектор - 16 Реакция - 3 Свободный вектор - 3 Связанный вектор - 3 Связь - 3 Сила - 2 Сила внешняя - 29 Сила внутренняя - 29 Сила инерции материальной точки – 35 Сила инерции механической системы - 35 Система параллельных сил - 9 Система сил - 3 Скользящий вектор - 3 Скорость (мгновенная) - 16 Сложное движение - 24 Собственный момент инерции – 32 Состояние движения - 2 Состояние покоя - 2 Среднее ускорение - 17 Средняя скорость - 16 Статика - 2 Статическая неопределимость – 12 Статическая определимость – 12 Стержень - 4 Теоретическая механика –2 Траектория - 16 Угловая скорость - 23 Угловое ускорение – 23 Уравновешенная система сил – 3 Ускорение (мгновенное) – 17 Условие равновесия сил - 9 Центр инерции - 36 Центр момента - 6 Центр параллельных сил - 10 Центр тяжести - 11 Шарнир - 5 Эквивалентная пара сил – 7 Эквивалентная система сил - 3
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 704. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Так как речь идет о материальной точке, то эти силы обязательно будут сходящимися, поэтому их всегда можно заменить равнодействующей
. Так как речь идет о материальной точке, то эти силы обязательно будут сходящимися, поэтому их всегда можно заменить равнодействующей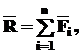 i = 1,…n.
i = 1,…n.
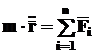 (10)
(10)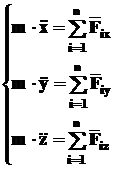 (11)
(11)
 (14)
(14)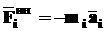 (19)
(19)