Подсчитаем момент пары сил относительно этой точки

поскольку  и точка выбиралась произвольно, теорема доказана.

Свойства пар сил:

1. Заданную пару сил можно свободно перемещать и поворачивать в плоскости ее действия.

2. Заданную пару сил можно переносить в любую точку твердого тела, сохраняя параллельность исходной плоскости ее действия.

3. Заданную пару сил всегда можно заменить другой парой сил, изменив обратно пропорционально расстояние между силами.

УСЛОВИЕ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ

Теорема С7 (лемма Пуансо). Силу, действующую на данное тело можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару сил с моментом, равным моменту исходной силы относительно новой точки ее приложения.

Рис. 9

Доказательство. Рассмотрим силу , действующую на тело в точке А (рис. 9а). Добавим в некоторой другой точке тела, например В, две силы  и , такие, что  и линии действия сил параллельны (рис. 9б). Очевидно, что  и  представляют собой уравновешенную систему сил и, следовательно, согласно аксиоме С5, состояние покоя тела не нарушится. Но силы  и  образуют пару сил и мы получаем систему, у которой имеется сила , приложенная в точке В, и пара сил с некоторым моментом m (рис. 9в), а равновесие тела сохраняется, ч. т. д.

ГЛАВНЫЙ ВЕКТОР - это сумма всех сил, действующих на рассматриваемую систему тел.

ГЛАВНЫЙ МОМЕНТ - это сумма моментов всех сил, действующих на рассматриваемую систему тел, относительно выбранного центра.

Теорема С8. Любую систему сил, действующих на данное тело, можно свести к действию одной силы, приложенной в любой наперед выбранной точке тела, и одной пары сил.

Доказательство. Рассмотрим тело, на которое действует произвольная система сил , ,…,  и пар сил с моментами , ,…,  (рис. 10а). Выбираем любую точку этого тела, например О. Перенесем все силы в эту точку. Согласно теореме С7 при этом необходимо добавить соответствующее количество пар сил с моментами , ,…,  (рис. 10б). Поскольку все силы собраны теперь в одной точке, их можно векторно сложить. В результате получим главный вектор системы

а также, используя свойства пар сил, можем сложить все действующие моменты пар сил и получим главный момент (рис. 10в)

Рис. 10

Теорема С9. Для того, чтобы тело под действием произвольной системы сил находилось в равновесии необходимо, чтобы главный вектор равнялся нулю и главный момент относительно произвольной точки тоже был равен нулю.

Доказательство. Из предыдущей теоремы С8 и следствия из аксиомы СЗ очевидно следует требуемое утверждение.

Следствие. При решении задач необходимо руководствоваться тем, что для равновесия тел необходимо  и  или же, спроектировав эти векторные равенства на соответствующие оси координат, получим для плоских задач систему из 3 уравнений равновесия

СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ

Система сил, линии действия которых параллельны, называются СИСТЕМОЙ ПАРАЛЛЕЛЬНЫХ СИЛ.

РАВНОДЕЙСТВУЮЩАЯ - одна сила, действие которой эквивалентно действию данной системы сил.

Лемма 1. Две параллельные силы всегда имеют равнодействующую.

Доказательство. Рассмотрим две параллельные силы  и  (рис.11а). Выберем некоторую точку А, лежащую между линиями действия этих сил, причем соответствующие расстояния  и  связаны следующей пропорцией .

Перенесем силы  и  параллельно самим себе в точку А. Согласно теореме С7, мы получим результирующую  и пару сил с моментом . Но правая часть выражения для момента в силу выбора точки А будет равна нулю, т.е. момент будет отсутствовать, а значит  будет действительно равнодействующей (рис. 11б). Если силы будут направлены в разные стороны, то доказательство сохраняется с маленьким изменением: точку А надо выбирать не между линий действия, а со стороны меньшей силы.

Рис. 11

Теорема С13. Система параллельных сил всегда имеет равнодействующую.

Доказательство. Очевидно, что, применяя лемму 1 к любым двум силам системы, мы получим из системы nсил систему n-1 сил. Повторив эту процедуру n-1 раз, мы наверняка получим только одну силу, заменяющую всю систему, т.е. равнодействующую.

Равнодействующая приложена к определенной точке, называемой ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ.

Координата центра параллельных сил

Рассмотрим систему , , ...,  параллельных сил (рис. 12). Заметим, что силы могут быть направлены и в противоположные стороны. Выберем систему координат таким образом, чтобы одна из осей была перпендикулярна линиям действия этих сил (ось X на рис. 12).

Рис. 12

Подсчитаем суммарный момент этих сил относительно начала координат (в приводимой формуле оперируем величинами сил)

.

Но на основании теоремы С13 мы знаем, что эти силы имеют равнодействующую, поэтому, согласно теореме С5 (теорема Вариньона), этот момент должен быть равен моменту равнодействующей относительно начала координат

следовательно, приравняв эти моменты, получим

По другим осям координат выражение получится точно таким же, только в правой части надо соответственно заменить х на у или z. Следовательно, можем записать полученную зависимость в векторной форме

                               (1)

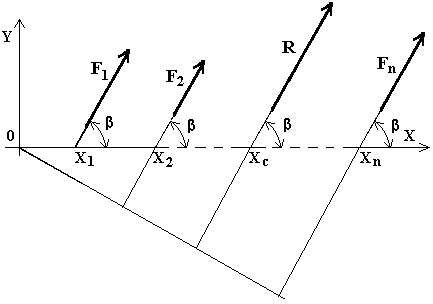
Заметим, что, если повернуть все силы на один и тот же угол b (рис. 13), а систему координат оставить на месте, то, повторив вывод формулы, получим то же самое значение, т.е. относительное положение центра параллельных сил не зависит от выбора системы координат.

Рис. 13

Центр тяжести

Силу тяжести фактически можно считать системой параллельных сил, поэтому для нее применимы все выше приведенные формулы.

Если тело является однородным, т.е. плотность его в любой точке тела одинакова, получаем, что вес элементарного объема тела , где - плотность тела, - объем i-ой части тела и тогда координата точки С по оси Х (остальные координаты находятся аналогично)