
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ДВИЖЕНИЕ В ЕСТЕСТВЕННОЙ СИСТЕМЕ КООРДИНАТ
Применяется ТОЛЬКО ТОГДА, КОГДА ИЗВЕСТНА ТРАЕКТОРИЯ ДВИЖЕНИЯ.
Рис. 19. Для регистрации движения применяется прямоугольная ЕСТЕСТВЕННАЯ СИСТЕМА КООРДИНАТ (рис. 19), которая характеризуется: - начало координат всегда совпадает с положением самой материальной точки (точка М на рис. 4); - первая ось (ось - вторая ось (ось - третья ось (ось Закон движения. В этом случае ЗАВИСИМОСТЬ ПО ВРЕМЕНИ РАССТОЯНИЯ ОТ ТЕКУЩЕГО ПОЛОЖЕНИЯ ТОЧКИ ДО НЕКОТОРОГО НАЧАЛЬНОГО, ИЗМЕРЕННОЕ ВДОЛЬ ТРАЕКТОРИИ, S(t) является ЕСТЕСТВЕННЫМ ЗАКОНОМ ДВИЖЕНИЯ (рис. 20а). Скорость. Для скорости тогда справедливо соотношение Разложение по осям вектора скорости в естественной системе координат Вектор скорости проектируется только на одну ось – ось Ускорение. Разложение по осям вектора скорости в естественной системе координат Определим величину проекций ускорения. Допустим, материальная точка движется в данный момент со скоростью 
Рис. 20
Спроектируем вектор и, следовательно, проекция ускорения на касательную (касательное или тангенциальное ускорение) аналогично
откуда
где Итак, окончательно КАСАТЕЛЬНОЕ УСКОРЕНИЕ И СКОРОСТЬ ВСЕГДА РАСПОЛАГАЮТСЯ НА ОДНОЙ ПРЯМОЙ, НО МОГУТ БЫТЬ НАПРАВЛЕНЫ В РАЗНЫЕ СТОРОНЫ (ЕСЛИ У НИХ РАЗНЫЕ ЗНАКИ). КАСАТЕЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ ВСЕГДА ПЕРПЕНДИКУЛЯРНЫ ДРУГ ДРУГУ. Связь между компонентами скоростей и ускорений. Поскольку вектора скорости и ускорения в каждый момент времени определяются однозначно, то между их компонентами при разложении в различных системах координат будут иметь место следующие зависимости
Кроме того, если продифференцировать первое из приведенных выражений, то легко получить
ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ
Прямолинейное движение. В этом случае траекторией движения точки является прямая линия, причем ее радиус кривизны равен бесконечности (
Векторы скорости и ускорения в этом случае располагаются на той же прямой, что и траектория, поэтому можно говорить, что они изменяются только численно, т. е. КАСАТЕЛЬНОЕ УСКОРЕНИЕ ХАРАКТЕРИЗУЕТ ИЗМЕНЕНИЕ СКОРОСТИ ПО ВЕЛИЧИНЕ. Равномерное криволинейное движение. Движение называется РАВНОМЕРНЫМ, если точка движется с постоянной по величине скоростью. Но, если скорость постоянная, то, следовательно, ее производная равна нулю, т. е. из (6) Так как в этом случае ускорение появляется только за счет изменения направления скорости, то, следовательно, НОРМАЛЬНОЕ УСКОРЕНИЕ ХАРАКТЕРИЗУЕТ ИЗМЕНЕНИЕ СКОРОСТИ ПО НАПРАВЛЕНИЮ. В этом случае легко определить закон движения, проинтегрировав выражение (1)
где S0 – координата начального положения материальной точки. ДВИЖЕНИЕ БЕЗ УСКОРЕНИЯ ( Равнопеременное криволинейное движение. Движение называется РАВНОПЕРЕМЕННЫМ, если оно происходит с постоянным касательным ускорением. Если ускорение положительно, такое движение иногда называют РАВНОУСКОРЕННЫМ, а если отрицательно – РАВНОЗАМЕДЛЕННЫМ. В этом случае, дважды проинтегрировав первое выражение из (6), получим где V0 – скорость точки в начальный момент времени. ДВИЖЕНИЕ МАТЕРИАЛЬНЫХ ТЕЛ
В теоретической механике рассматриваются ТОЛЬКО АБСОЛЮТНО ТВЕРДЫЕ ТЕЛА. Движение всех материальных тел можно определенным образом классифицировать и рассматривать, как ведут себя характеристики движения применительно к каждому классу движения. Причем будем считать движение тела определенным только в том случае, если нами определены характеристики движения любой точки рассматриваемого тела. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
Движение тела называют ПОСТУПАТЕЛЬНЫМ, если любой отрезок, взятый внутри тела, остается, параллелен самому себе все время движения. Рассмотрим некоторое тело, которое движется поступательно в выбранной системе координат (рис. 21). Выберем некоторый отрезок АВ внутри тела. Положение точек А и В определяют радиус – вектора
Рис. 21 По определению поступательного движения и из предположения, что мы имеем дело только с абсолютно твердыми телами, следует, что вектор Если продифференцировать предыдущее равенство, то получим Продифференцировав еще раз, также получим Таким образом, ПРИ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ ТЕЛА ЗАКОНЫ ДВИЖЕНИЯ ВСЕХ ЕГО ТОЧЕК ОТЛИЧАЮТСЯ НА ПОСТОЯННУЮ ВЕЛИЧИНУ, ТРАЕКТОРИИ ПРИ НАЛОЖЕНИИ СОВПАДАЮТ, СКОРОСТИ ВСЕХ ТОЧЕК РАВНЫ МЕЖДУ СОБОЙ И УСКОРЕНИЯ ТАКЖЕ РАВНЫ МЕЖДУ СОБОЙ. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Движение тела называются ВРАЩАТЕЛЬНЫМИ, если при движении тела существуют, по крайней мере, две (а если тело плоское и движется в своей плоскости – то одна) точки тела (или неизменно с ним связанные), которые остаются неподвижными все время движения. Линия, проходящая через эти две точки (если движение плоское, то перпендикулярно плоскости движения), называется ОСЬ ВРАЩЕНИЯ. Рассмотрим некоторое тело, которое движется вращательно (рис. 22а) и точки А и В – неподвижны. Все точки, лежащие на оси вращения, неподвижны, так как если бы было не так, т.е. точка С имела некоторую скорость VС Рассмотрим точки, лежащие не на оси вращения, например, точку М (рис. 22а). Расстояние от этой точки до оси вращения – LМС. Так как точка С неподвижна, а тело абсолютно твердое, то LМС величина постоянная, и, следовательно, траектория точки М – окружность. Все точки тела, удаленные на расстоянии LМС от оси вращения, должны двигаться по одинаковым траекториям (окружности) и с одинаковыми по величине скоростями и ускорениями (иначе изменилось бы их взаимное расположение, т.е. тело деформировалось, а это противоречило бы гипотезе об абсолютной жесткости рассматриваемого тела). Таким образом, все точки, принадлежащие любому цилиндрическому сечению внутри тела, образующая которого параллельна оси вращения, имеют одинаковые характеристики движения.
Рис. 22 Осталось рассмотреть, чем отличается движение точек, лежащих на одном луче, например СМ. Пусть точка М переместится в положение М1(рис. 22б). Луч СМ должен остаться прямым, следовательно, положение луча СМ удобно характеризовать одной характеристикой – углом поворота - угловая скорость - угловое ускорение Тогда перемещение произвольной точки С в естественной системе координат может быть выражено Если продифференцировать это выражение, получим выражение для скорости Если продифференцировать еще раз, то получим выражение для касательного ускорения Нормальное ускорение определяется соотношением Поскольку нормальное и касательное ускорение всегда перпендикулярны друг другу, то модуль полного ускорения может быть вычислен Таким образом, определены характеристики всех точек тела при его вращательном движении. СЛОЖНОЕ ДВИЖЕНИЕ ТЕЛ
До сих пор при изложении кинематики не принимался в рассмотрение один очень важный вопрос, а именно: как влияет на характеристики движения тела движение самой системы отсчета? Вопрос актуальный, так как в нашем распоряжении (в земных условиях) нет практически систем координат неподвижных или движущихся с постоянной скоростью (земная поверхность участвует во вращении нашей планеты вокруг собственной оси, сама планета движется вокруг Солнца и т. д.). Поэтому важно выяснить степень влияния движения самой системы отсчета, чтобы при необходимости вносить поправку в расчеты. Движение тела называется СЛОЖНЫМ, если оно регистрируется в подвижной системе координат. При этом движение тела относительно системы координат называется ОТНОСИТЕЛЬНЫМ, а движение самой системы координат – ПЕРЕНОСНЫМ. Рассмотрим движение точки в подвижной системе координат (рис. 24). За малый промежуток времени Рис. 24 Поскольку речь идет о малых перемещениях за малые промежутки времени, с незначительной погрешностью можно считать, что Теорема Кориолиса Если продифференцировать равенство (9), то учитывая, что относительная скорость изменяется при изменении переносной и наоборот, в правой части получится не два слагаемых, а четыре Первое слагаемое в правой части - это собственно относительное ускорение, четвертое - переносное ускорение, а второе и третье - результат взаимного влияния переносного и относительного движения друг на друга. Опуская здесь строгое доказательство, которое впервые получил Кориолис, приводим окончательный результат где ТЕОРЕМА К3. Абсолютное ускорение точки, участвующей в сложном движении, равняется векторной сумме относительного, переносного и кориолисова ускорений. Доказательство. Без доказательства. По свойствам векторного произведения Величина кориолисова ускорения может быть вычислена по формуле где Кориолисово ускорение будет отсутствовать ( 1) 2) 3) Во всех остальных случаях сложного движения кориолисово ускорение присутствует. В частности, при движении тел по поверхности Земли на них действует кориолисово ускорение, при малых скоростях незначительное.
Д И Н А М И К А ДИНАМИКА изучает поведение материальных тел как результат их взаимодействия с другими телами. Так как мерой взаимодействия является сила, то поведение сил и изменение характеристик движения во времени должны быть взаимосвязаны. При рассмотрении статики силы считались постоянными величинами, в динамике будем учитывать, что сила – величина переменная. Все задачи динамики можно условно разделить на две категории: - зная характеристики движения, определить силы, вызвавшие такое движение (ПРЯМАЯ ЗАДАЧА); - зная силы, определить характеристики движения (ОБРАТНАЯ ЗАДАЧА).
АКСИОМЫ
Те аксиомы, которые введены в статике и кинематике, сохраняют свой смысл, Однако их надо дополнить новыми. Аксиома Д1. Любое материальное тело можно представить как совокупность конечного числа материальных точек. Аксиома Д2. Если силы, действующие на материальную точку, уравновешены или вовсе отсутствуют, то эта точка сохраняет состояние покоя или движется равномерно и прямолинейно (по инерции). Движение равномерное и прямолинейное называется ИНЕРЦИОННЫМ ДВИЖЕНИЕМ. Система координат, в которой выполняется аксиома Д1, называется ИНЕРЦИОННАЯ СИСТЕМА ОТСЧЕТА. На практике следует учитывать, что безусловно инерционной можно считать только систему координат с центром в центре масс Солнца и осями, направленными на удаленные внегалактические объекты. Систему координат, располагающуюся на поверхности земли, можно считать инерционной лишь условно, так как погрешность расчетов подавляющего большинства задач о движении тел вблизи поверхности Земли может быть достаточно велика. Аксиома Д3. Если на материальную точку действует сила, то эта точка будет двигаться с ускорением, прямо пропорциональным этой силе. Коэффициент пропорциональностиm между силой Поскольку в теоретической механике рассматриваются тела, движущиеся со скоростями только гораздо меньше скорости света, то МАССУ можно СЧИТАТЬ ПОСТОЯННОЙ ВЕЛИЧИНОЙ. Возьмем две материальные точки с различными массами, например m1>m2, и подействуем на каждую из них одной и той же силой Видим, что чем больше масса точки, тем медленнее она будет двигаться под действием одной и той же силы при прочих равных условиях. ИНЕРТНОСТЬ – это способность тел сопротивляться попыткам изменить их состояние. МАССА ЯВЛЯЕТСЯ МЕРОЙ ИНЕРТНОСТИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛ. Чем больше масса, чет труднее привести тело в движение, но и труднее затем остановить его.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 827. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

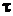 ) всегда располагается на касательной к траектории движения и направлена в ту сторону, куда движется материальная точка (КАСАТЕЛЬНАЯ);
) всегда располагается на касательной к траектории движения и направлена в ту сторону, куда движется материальная точка (КАСАТЕЛЬНАЯ); ) всегда располагается на нормали к траектории движения (всегда перпендикулярна касательной к траектории и находится в плоскости движения) и направлена в сторону вогнутости траектории (НОРМАЛЬ);
) всегда располагается на нормали к траектории движения (всегда перпендикулярна касательной к траектории и находится в плоскости движения) и направлена в сторону вогнутости траектории (НОРМАЛЬ); ) всегда располагается на бинормали к траектории (т.е. перпендикулярна и касательной, и нормали) и направлена так, чтобы образовывать с первой и второй осью правую систему координат (БИНОРМАЛЬ).
) всегда располагается на бинормали к траектории (т.е. перпендикулярна и касательной, и нормали) и направлена так, чтобы образовывать с первой и второй осью правую систему координат (БИНОРМАЛЬ).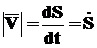 (5)
(5) . Учитывая особенности вектора скорости, получим
. Учитывая особенности вектора скорости, получим
 .
.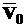 и находится в некоторой точке пространства М, имеющей координату S (рис. 20а). Через момент времени
и находится в некоторой точке пространства М, имеющей координату S (рис. 20а). Через момент времени 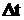 точка переместится в положение К с координатой S=S +
точка переместится в положение К с координатой S=S +  S и скоростью
S и скоростью 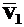 . Переместим скорость
. Переместим скорость 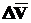 (рис. 20б).
(рис. 20б).
 и
и  , то с точностью до бесконечно малых величин можно считать, что
, то с точностью до бесконечно малых величин можно считать, что



 - радиус кривизны траектории.
- радиус кривизны траектории. (6)
(6)


 ), и, следовательно, из (6) получаем
), и, следовательно, из (6) получаем .
. .
.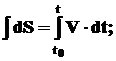

 ) ВОЗМОЖНО ЛИШЬ В СЛУЧАЕ РАВНОМЕРНОГО ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ.
) ВОЗМОЖНО ЛИШЬ В СЛУЧАЕ РАВНОМЕРНОГО ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ.
 ;
; S =
S = 
 и
и  . Дополним рисунок вектором
. Дополним рисунок вектором  . Тогда очевидно можно записать, что
. Тогда очевидно можно записать, что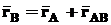 .
.


 0, то в следующий момент времени эта точка сместилась бы по направлению скорости в другую точку пространства и, следовательно, не смогла бы сохранить одновременно и расстояние ВС,и расстояниеАС, т.е. был бы нарушен принцип абсолютно твердого тела. Значит точка С - неподвижна.
0, то в следующий момент времени эта точка сместилась бы по направлению скорости в другую точку пространства и, следовательно, не смогла бы сохранить одновременно и расстояние ВС,и расстояниеАС, т.е. был бы нарушен принцип абсолютно твердого тела. Значит точка С - неподвижна.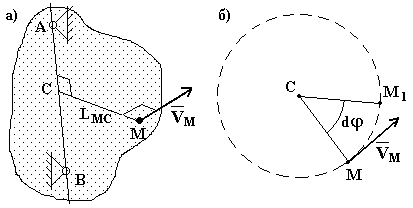
 , поэтому ЗАКОН ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ – ЭТО ЗАВИСИМОСТЬ УГЛА ПОВОРОТА ОТ ВРЕМЕНИ
, поэтому ЗАКОН ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ – ЭТО ЗАВИСИМОСТЬ УГЛА ПОВОРОТА ОТ ВРЕМЕНИ  . При этом дополнительно вводятся характеристики:
. При этом дополнительно вводятся характеристики: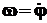 ;
; .
.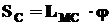
 (7)
(7) (8)
(8) (9)
(9)
 точка переместится из положения А в положение В, но одновременно с этим ведь перемещалась и система координат. Следовательно фактически точка окажется в положении С, т. е.
точка переместится из положения А в положение В, но одновременно с этим ведь перемещалась и система координат. Следовательно фактически точка окажется в положении С, т. е.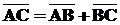

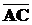 соответствует вектору абсолютной скорости
соответствует вектору абсолютной скорости  ,
,  скорости относительного движения
скорости относительного движения  ,
,  скорости переносного движения
скорости переносного движения  , т. е.
, т. е. (9)
(9)

 кориолисово ускорение, равное удвоенному векторному произведению угловой скорости переносного движения на линейную скорость относительного.
кориолисово ускорение, равное удвоенному векторному произведению угловой скорости переносного движения на линейную скорость относительного. располагается так, чтобы быть перпендикулярным и
располагается так, чтобы быть перпендикулярным и  , и
, и 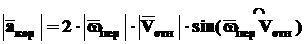
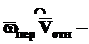 острый угол между векторами
острый угол между векторами  и
и  .
. ), если
), если это значит, что система координат движется поступательно или покоится;
это значит, что система координат движется поступательно или покоится;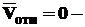 это значит, что тело покоится в выбранной системе координат;
это значит, что тело покоится в выбранной системе координат; это значит, что точка движется в данный момент параллельно оси переносного вращения.
это значит, что точка движется в данный момент параллельно оси переносного вращения. и ускорением
и ускорением 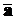 называется МАССА материальной точки.
называется МАССА материальной точки. .
.