
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Практическое занятие 2. Законы распределения случайных величинПлан занятия: 1. Повторение изученных теоретических разделов 2. Решение типовых задач у доски 3. Самостоятельное решение задач 4. Обсуждение решения и анализ основных ошибок 5. Доклады студентов по теме практического занятия Теоретические сведения
Отказы ПО являются случайными событиями. Время отказа ПО является случайной величиной. Плотность распределения случайной величины x обладает следующими свойствами. Плотность распределения случайной величины всегда неотрицательна .
Интеграл от функции плотности на всей числовой оси ( -∞;+∞) равен 1:
Плотность распределения случайной величины x связана с функцией ее распределения следующими соотношениями:
Плотность распределения случайной величины называют также дифференциальной характеристикой, функцию распределения случайной величины называют интегральной характеристикой. Функция распределения случайной величины X равна вероятности того, что значение случайной величины будет меньше или равно X.
Функция распределения случайной величины X обладает следующими свойствами. Функция распределения случайной величины всегда неотрицательна.
Функция распределения случайной величины является монотонно возрастающей функцией, причем F(+∞) = 1 . Для описания распределения случайной величины обычно используют один из стандартных законов, которые задают зависимость f(x) и F(x) в аналитическом виде. Наиболее часто в технике используют следующие законы распределения случайных величин: - равномерный, - нормальный (гауссовский), - показательный (экспоненциальный). В качестве параметров распределения используют математическое ожидание M(x) и дисперсию D(x) случайной величины.  Равномерный закон распределения случайной величины Плотность распределения случайной величины при равномерном законе распределения имеет вид:
Функция распределения случайной величины при равномерном законе распределения имеет вид:
Параметры равномерного распределения:
Равномерное распределение случайной величины на отрезке [0,1] обозначается как U[0,1] и называется стандартным равномерным распределением. |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 382. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
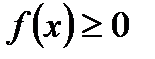 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3)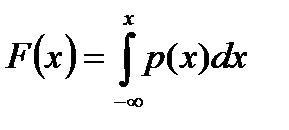 (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9)