
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
История возникновения и развития комбинаторикиСтр 1 из 20Следующая ⇒ Содержание Понятие комбинаторной задачи……………………….………...13 История возникновения и развития комбинаторики………...13 Конечные множества…………………………...……………..…..24 Операции над множествами……………………………………...25 Декартово произведение множеств А и В………………………33 Задачи для самостоятельного решения…………………………34 Нахождение числа всех подмножеств данного множества…...36 Понятие факториала………………………………….……….......38 Задания для самостоятельного решения…………….……….....39 Правила суммы и произведения……………………….………...40 Задачи для самостоятельного решения………………….….......45 Вопросы для самопроверки……………………………….….......48 Виды соединений без повторений……………………………49 Перестановки без повторений…………………………….….......49 Задачи для самостоятельного решения…….……………..…….52 Размещения без повторений………………………………….......52 Задачи для самостоятельного решения……………………........54 Сочетания без повторений………………………………...….......56 Свойства чисел Задачи для самостоятельного решения……………………........61 Почему 0!=1?......................................................................................62 Вопросы для самопроверки………………………………….…...62 Виды соединений с повторениями……………………….…..65 Сочетания и размещения с повторениями…………..…………65 Перестановки с повторениями……………………….………......69 Задачи для самостоятельного решения…..…………………......70 Бином Ньютона…………………….……………………….……...71 Задачи для самостоятельного решения…………………………77 Вопросы для самопроверки………………………………………77  Контрольные вопросы……………………………………….........78 Примеры решения некоторых комбинаторных задач...….…..79 Задачи для самостоятельного решения…………………………88 Примеры решения некоторых комбинаторных задач...….…. 90 Задачи для самостоятельного решения…………………………93 Примеры решения некоторых комбинаторных задач...….…..94 Задачи для самостоятельного решения…………………………96 Примеры решения некоторых комбинаторных задач...….…..97 Задачи для самостоятельного решения…………………………99 Формула включений и исключений…………………………...100 Примеры решения комбинаторных задач...…………………..102 Задачи для самостоятельного решения по курсу «Комбинаторика»………………………………………………….....…….........112 Задачи для самостоятельного решения………………..….…...143 Понятие комбинаторной задачи Комбинаторика – один из разделов дискретной математики, который приобрел важное значение, в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике, кибернетике. Комбинаторные соображения лежат в основе решения многих задач теории вероятностей – важного раздела современной математики, посвященного изучению случайных явлений. Решая разнообразные жизненные задачи, мы нередко сталкиваемся с теми, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи, требующие такого решения, называются комбинаторными. Область математики, в которой изучают комбинаторные задачи, называюткомбинаторикой. «Комбинаторика – раздел математики, посвящённый решению задач выбора и расположения элементов, обычно конечного, множества в соответствии с заданными условиями»[1]. Комбинаторика (теория соединений) – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, удовлетворяющих тем или иным условиям, можно составить из заданных объектов. Комбинаторика изучает количество комбинаций, удовлетворяющих определенным условиям, которые можно составить из элементов заданного конечного множества. «Особая примета» комбинаторных задач - вопрос, который можно сформулировать так, чтобы он начинался словами: «Сколькими способами…»[2]. В данном разделе математики решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств.
История возникновения и развития комбинаторики Ориентация на общее развитие личности в процессе образования включает элементы истории математики. Использование историко-математического материала на занятиях содействует повышению их общей эффективности. Математика предстает перед студентами не сформировавшейся наукой, а в процессе создания, в динамике. История науки позволяет учащимся увидеть ее движущие силы, наблюдать в действии взаимосвязь и взаимообусловленность научного познания и практической деятельности человека. «Лучший метод для предвидения будущего развития математических наук заключается в изучении истории и нынешнего состояния этих наук» отмечал А.Пуанкаре[3]. С этой точки зрения, целесообразно начинать изучение комбинаторики с истории возникновения и развития данной науки. Прежде, чем та или иная область знания сформируется в особую науку, она проходит длительный период накопления эмпирического материала, период развития в недрах другой, более общей науки, и затем выделяется в самостоятельную науку. Не является исключением и наука про общие законы комбинирования и образования различных конфигураций объектов, получившая название «комбинаторика». Еще в доисторическую эпоху люди столкнулись с проблемой выбора тех или иных объектов, расположения их в определенном порядке, нахождения среди различных расположений подходящих. Например, во время охоты необходимо было выбрать наилучшее расположение охотников, во время битвы – расположение воинов. Они находили свое применение и в часы досуга. «Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие умения рассчитывать, составлять планы и опровергать планы противника. О таких играх английский поэт У. Вордсворт писал:
Среди вещей египетского фараона Тутанхамона, который был захоронен 35 веков назад, в пирамиде, были найдены разграфленные доски, с 3 горизонталями и 10 вертикалями, и фигурки для древней игры «сенет». Ее правила не дошли до наших дней. В дальнейшем в таких играх, как нарды, шахматы и различных их вариантах (китайские и японские шахматы, японские шашки «го» и т.д.), необходимо было рассматривать различные сочетания передвигаемых фигур. И, как правило, выигрывал тот, кто лучше решал задачи по наиболее удачному расположению фигур. Вопросы, связанные с комбинаторикой, встречаются в китайских рукописях, относящихся к XIII XII вв. до н.э.[5] Китайцы считали, что «все в мире является сочетанием двух начал – мужского и женского, которые обозначались символами ― и −−.». В рукописи «Же Ким» («Книга перестановок») показаны различные соединения этих знаков по два и по три.
«Восемь рисунков из трех рядов символов изображали землю, горы, воду, ветер, грозу, огонь, облака и небо (некоторые рисунки имели и иные значения)». Неудивительно поэтому, что сумма первых 8 натуральных чисел воплощала в представлениях древних китайцев весь мир. Позже были составлены 64 фигуры, содержавшие пять рядов черточек. Видимо, автор рукописи «Же Ким» заметил удвоение числа рисунков при добавлении одного ряда символов. Это можно рассматривать как первый общий результат комбинаторики[6]. Из рукописи «Же Ким» мы можем также узнать, что император Ию, который жил примерно 4000 лет назад, «нашел на берегу реки священную черепаху, на ее панцире был изображен рисунок из черных и белых кружков».
Если заменить каждую фигурку соответствующим числом, возникнет такая таблица: Если сложить числа в каждой строке, столбце и диагонали, то получится одна и та же сумма 15. В древности китайцы давали мистическое толкование числам. Когда китайцы открыли таблицу с такими чудесными свойствами, то она произвела на них неизгладимое впечатление. Данный рисунок назвали «ло-шу», стали употреблять его при заклинаниях и считать магическим символом. «Магическим квадратом» теперь называют любую квадратную таблицу с одинаковыми суммами по каждой строке, столбце и диагонали. Комбинаторные задачи, касавшиеся перечисления небольших групп предметов, решали греки. Аристотель описал без пропусков все виды правильных трехчленных силлогизмов, а его ученик Арисксен из Тарента перечислил различные комбинации длинных и коротких слогов в стихотворных размерах. Живший в IV в. н.э. математик Папп рассматривал число пар и троек, которые можно получить из трех элементов, допуская их повторения. В XVIII веке происходит расцвет арабской науки. Арабами были переведены многие работы греческих и римских ученых. Арабские алгебраисты, при извлечении корней, вывели формулу для степени суммы двух чисел, которая в истории математики известна нам под названием «бином Ньютона». Историки считают, что эту формулу знал поэт и математик Омар Хайам (XI–XII вв.) Ее в XIII веке приводит в своих трудах Насир ад-Динат-Туси, а в XV веке она была исследована Джемшид ибн Масуд аль-Каши. Как сообщают нам некоторые европейские источники, восходящие к арабским оригиналам, «коэффициенты этой формулы высчитывали следующим образом: брали число 10001 и возводили его во вторую, третью, четвертую, …, девятую степени»[7]. Составлялась таблица, имеющая следующий вид:
При опускании в таблице лишних нулей получается треугольная таблица из биномиальных коэффициентов. Арабские ученые знали и основное свойство элементов этой таблицы, выражающееся формулой В вычислении биномиальных коэффициентов не отставали от арабов и китайские математики. Уже к XIII веку в книге алгебраиста Чжу Ши-дза «Яшмовое зеркало» приводится таблица таких чисел, вплоть до n=8. Известно также, что «в VIII веке астроном И.Синь вычислил количество различных расположений фигур в игре, которая напоминала шахматы». Интерес к сочетаниям проявлялся и в Индии. В VII веке индийский математик Бхаскара в книге «Лилавати», изучая проблемы комбинаторики, писал о применении перестановок к подсчету вариаций размера в стихосложении, различных расположений в архитектуре и т. п. В его работе мы можем найти правила для отыскания числа перестановок и сочетаний нескольких предметов. При этом им также рассматривается и случай, когда в перестановках есть повторяющиеся элементы. В результате развития торговли с Востоком в начале XII века арабская наука проникает в Западную Европу. В то время арабское учебное заведение окончил Леонардо – сын пизанского купца, торговавшего в Алжире. «Он написал книгу «Liber Abaci», которая вышла 1202 году. Леонардо получил прозвище Фибоначчи, он привел в систему всю арифметику арабов», некоторые сведения по геометрии Евклида и добавил к ним результаты своих изысканий. В работе Фибоначчи излагаются новые комбинаторные задачи, например, «об отыскании наименьшего количества гирь, с помощью которых можно получить любой целый вес от 1 до 40 фунтов»[8]. Леонардо уделял внимание и отысканию целых решений уравнений. Рассмотрение аналогичных задач в последствии привело к появлению количества натуральных решений систем уравнений и неравенств, имеющих право на рассмотрение как на одну из глав комбинаторики. Леонардо выявил новую последовательность, наряду с известными еще со времен греческих математиков, арифметической и геометрической прогрессий, каждый член которых получался по определенным правилам из предыдущих, члены новой последовательности были связаны друг с другом соотношением Существовавшие еще в глубокой древности азартные игры, получившие особенное распространение после крестовых походов, способствовали развитию комбинаторики. Наибольшее распространение получила игра в кости – два или три кубика с нанесенными на них очками бросали на стол, и ставку брал тот, у кого выпала большая сумма очков. Несмотря на грозные запреты церкви, азартные игры все же развивались. В любом городе можно было наблюдать картину, которая описана в «Божественной комедии» Данте:
В кости играли еще этруски жители Мохенджо-Даро, это известно из археологических раскопок. Однако, эти древние игры не подвергались математическому исследованию довольно долго. Позже некоторые игроки, которые наиболее часто играли в кости, подметили, что одни суммы очков выпадают часто, а другие – редко. Были составлены таблицы, показывавшие, сколькими способами можно получить то или иное число очков. Сначала допускалась ошибка – подсчитывали только число различных сочетаний, дававших данную сумму. Например, при бросании двух костей сумма 6 получается из сочетаний (1, 5), (2, 4), (3, 3), а сумма 7 – из сочетаний (1, 0), (2, 5), (3, 4). Так как три сочетания были различны в обоих случаях, то напрашивался ошибочный вывод о том, что суммы очков 6, 7 и 8 (также получаемая из трех сочетаний костей) должны выпадать одинаково часто. Но согласно опыту 7 очков выпадает чаще. Сочетание (3, 3) при бросании двух костей может быть получено единственным способом, а сочетание (3, 4) – двумя способами. Именно благодаря этому, сумма 7 выпадает наиболее часто. Таким образом, оказалось, что надо учитывать не только сочетание очков, но и их порядок. Этими вопросами занимались такие известные итальянские математики XVI века, как Д. Кардано, Н. Тарталья и др. Наиболее полно исследовал данный вопрос в XVII веке Галилео Галилей, но его рукопись оставалась неопубликованной до 1718 г. В 1713 г. была опубликована книга «Искусство предположений» Якоба Бернулли, в которой указывались формулы для числа размещений из Работы Б.Паскаля[9] и П.Ферма[10] ознаменовали рождение двух новых ветвей математической науки – комбинаторики и теории вероятностей. Ранее комбинаторные проблемы лишь затрагивались в общих трудах по астрологии, логике и математике или большей частью относились к области математических развлечений. В 1666 году В. Лейбниц[11] публикует «Диссертацию о комбинаторном искусстве», в которой впервые появляется термин «комбинаторный». Этот математический труд Лейбница должен был стать лишь началом большой работы, о которой он часто упоминал в своих письмах и печатных трудах. В. Лейбниц планировал для комбинаторики многочисленные приложения: к играм, статистике, к кодированию и декодированию, к теории наблюдений. Он считал, что комбинаторика должна заниматься «одинаковым и различным, похожим и непохожим, абсолютным и относительным расположением, в то время как обычная математика занимается большим и малым, единицей и многим, целым и частью». Иными словами, под комбинаторикой В. Лейбниц понимал примерно то, что мы теперь называем дискретной математикой. К области комбинаторики В. Лейбниц относил и «универсальную характеристику» – математику суждений, то есть прообраз нынешней математической логики. Проекты В. Лейбница казались несбыточными математикам его времени, но сейчас, после создания быстродействующих вычислительных устройств, многие его планы стали претворяться в жизнь, а дискретная математика выросла в своем значении и начала соперничать с математическим анализом. Замечательные достижения в области комбинаторики принадлежат одному из величайших математиков XVIII века Леонарду Эйлеру[12], швейцарцу, прожившему почти всю жизнь в России, где он был членом Петербургской академии наук. Основная часть научной работы Л. Эйлера посвящена математическому анализу, в котором он проложил новые пути, создал целый ряд новых областей и подвел итоги исследованиям в других областях. Но у Л. Эйлера хватало времени размышлять и над задачами, которые, казалось бы, не заслуживали его внимания,– о том, можно ли обойти мосты в Кенигсберге (ныне Калининграде) так, чтобы не побывать дважды на одном и том же мосту? – можно ли поставить 36 офицеров из 6 разных полков так, чтобы в каждой шеренге и каждой колонне было по одному офицеру каждого воинского звания из каждого полка? – сколькими способами можно разбить данное число на слагаемые и т.д. Работа о мостах явилась зерном, из которого впоследствии выросли топология и теория графов, задача об офицерах оказалась сейчас связанной с планированием экспериментов, а методы, использованные при решении задачи о разбиении чисел, после длительного и сложного пути развития превратились в науку об интегральных преобразованиях, применяемую для решения уравнений математической физики. После работ Б.Паскаля и П.Ферма, Г.Лейбница и Л.Эйлера можно было уже говорить о комбинаторике как о самостоятельном разделе математики, тесно связанном с другими областями науки, такими, как теория вероятностей, учение о рядах и т.д. Таким образом, комбинаторика как самостоятельная ветвь математики возникла в XVII веке. На протяжении долгого времени основную роль в изучении мироздания играл математический анализ – дифференциальное и интегральное исчисления, дифференциальные уравнения, уравнения математической физики, вариационное исчисление и т.д. Все процессы рассматривались как непрерывные, чтобы можно было применять к ним развитый аппарат математики непрерывного. С появлением быстродействующих вычислительных машин такие абстрактные области математики, как математическая логика, общая алгебра, стали прикладными. Тогда для составления алгоритмических языков, на которых стали писать программы для машин, понадобились специалисты именно в этих областях математики. Произошло изменение соотношения между дискретной и классической математикой. Изменилась и роль древнейшей области дискретной математики – комбинаторики. Если раньше комбинаторика применялась для составления занимательных задач, для кодирования и расшифровки древних письменностей, то со временем она превращается в важнейшую область математического знания.
Конечные множества Большинство задач комбинаторики можно сформулировать как задачи теории конечных множеств. Поэтому целесообразно напомнить некоторые положения «теории конечных множеств». Всякая совокупность объектов произвольного рода образует множество. При этом сами объекты называют элементами данного множества. Множества обозначают большими латинскими буквами, их элементы – малыми латинскими буквами. Запись Множество считают определённым, если о любом объекте можно сказать, является он элементом данного множества или нет. По количеству элементов множества делят на пустые, конечные и бесконечные. Пустым называют множество, не содержащее ни одного элемента. Обозначают такое множество символом Æ. Если каждый элемент множества В принадлежит множеству А, то В называют подмножеством множества А. Обозначают: Читают: множество В входит в множество А или множество Теорема 1. Если ÿ Доказательство проведем методом «от противного». Пусть множества Теорема доказана. На основе теоремы 1основан метод доказательства равенства множеств, который называют«методом включения». Непустое подмножество Несобственными подмножествами множества Бесконечным называют множество равномощное некоторому собственному подмножеству. Конечным называют множество, которое не равномощно ни какому собственному подмножеству. Количество элементов множества Операции над множествами Суммой или объединением множеств Обозначают: C=A Если A Операцию нахождения объединения называют сложением множеств. Сложение множеств обладает свойствами коммутативности и ассоциативности. То есть, для произвольных множеств A A Первое из этих равенств вытекает из определения суммы. Второе есть следствие того, что A Множество Обозначают: C=A Если A Операцию нахождения пересечения называют пересечением множеств. Пересечение множеств коммутативно и ассоциативно. То есть, для произвольных множеств A A Напомним, что операции объединения и пересечения множеств обладают также свойством дистрибутивности. То есть, для произвольных множеств A A Наглядно операции над множествами можно иллюстрировать, изображая множества в виде кругов (их называют «кругами Эйлера» или «диаграммами Эйлера-Венна») или других фигур на плоскости. Разностью множеств Обозначают Операцию нахождения разности множеств называют вычитанием множеств. Вычитание множеств не коммутативно и не ассоциативно, то есть, существуют множества
Сформулируем и докажем некоторые утверждения теории множеств, необходимые для изложения дальнейшего материала. Лемма 1. Для любых множеств А и В справедливо равенство: B=(A ÿ Докажем данное утверждение методом включения, то есть покажем что B Таким образом, лемма 1 доказана. Лемма 2. Для произвольных множеств А и В справедливо равенство: (A ÿ Доказательство проведем методом «от противного». Предположим, что равенство (2) не выполняется. Тогда, существует хотя бы один элемент, который принадлежит множеству (A Пусть x Лемма 2 доказана. Теорема 2.Число элементов в объединении двух непересекающихся множеств равно сумме чисел элементов в каждом из них, то есть, если п(A)=a, n (B)=b и A Замечание. Данное утверждение справедливо для любого конечного числа попарно непересекающихся конечных множеств. n(A Лемма 3. Для любых множеств А и В справедливо равенство: n (B \ A) = n (B) – n (A ÿ Согласно лемме 1 B=(A Отсюда, n(B \ A)=n(B)–n(A Теорема 3. Число элементов в объединении двух произвольных конечных множеств равно сумме чисел элементов в каждом из них, уменьшенной на число элементов в пересечении данных множеств, то есть n (A ÿ Докажем сначала, что для произвольных множеств A и B выполняется равенство A Пусть x произвольный элемент множества A Аналогично доказывается включение A Докажем теперь, что для любых множеств A и B выполняется равенство A Предположим, что существуют множества A и B такие, что A Таким образом, учитывая равенства (*), (**) и теорему 2, получаем n(A Теорема. 3 доказана. Рассмотрим задачу, при решении которой используются приведенные теоретические положения. Задача 1. В классе «Грифендор» учатся 40 студентов. У них есть возможность посещать предметы по выбору. 23 студента занимаются наукой прорицания, 11 занимаются предметом защиты от темных сил и 8 студентов, используя часы для возвращения в прошлое, занимаются и наукой прорицания, и предметом защиты от темных сил. Есть ли в группе студенты, которые не занимаются ни наукой прорицания, ни предметом защиты от темных сил? Решение.Анализ условия показывает, что в задаче речь идёт о множестве А – студентов группы (n(A)=40), множестве В – студентов, которые занимаются наукой прорицания (n(B)=23), множестве С – студентов, посещающих уроки по защите от темных сил (n(C)=11).
Чтобы найти число студентов, которые не занимаются ни наукой прорицания, ни предметом защиты от темных сил необходимо из числа всех студентов группы вычесть число студентов, занимающихся или наукой прорицания, или предметом защиты от темных сил, то есть число n(B п(B Так как всего в группе 40 студентов, то не занимаются ни наукой прорицания, ни предметом защиты от темных сил: 40–6=14 (студентов). Ответ: 14 студентов, которые не занимаются ни наукой прорицания, ни предметом защиты от темных сил. Теорема 3.1. Справедлива следующая формула для нахождения числа элементов в объединении трех произвольных конечных множеств: n(A ÿ Данное утверждение является следствием теоремы 3. В самом деле, так как сложение множеств обладает свойством ассоциативности, то A n (A Применяя далее свойства дистрибутивности пересечения множеств относительно сложения, ассоциативности и идемпотентности пересечения множеств, а также теорему 3, получим: n((A −n((A и n(A Таким образом, подставляя равенства (**) и (***) в (*), получаем: n(A =n(A)+n(B)–n(A =n(A)+n(B)+n(С)–n(A Теорема. 3.1 доказана. Задача 2. Из 28 студентов группы 14 человек занимаются плаванием, 18 человек – баскетболом, 12 студентов – легкой атлетикой, 8 – плаванием и баскетболом, 7 – легкой атлетикой и баскетболом, 6 – плаванием и легкой атлетикой, 3 студентов занимаются и плаванием, и баскетболом, и легкой атлетикой. Сколько в группе студентов, которые не занимаются ни одним из данных видов спорта? Решение.Анализ условия показывает, что в задаче речь идёт о нескольких множествах. Пусть К – множество студентов группы (n(K)=28), В – множество студентов, занимающихся плаванием (n(B)=14), С – множество студентов, занимающихся баскетболом (n(C)=18), А – множество студентов, занимающихся легкой атлетикой (n(А)=12), М – множество студентов, занимающихся плаванием и легкой атлетикой (n(М)=6), Р – множество студентов, занимающихся баскетболом и легкой атлетикой (n(Р)=7), У – множество студентов, занимающихся плаванием и баскетболом (n(У)=8), L – множество студентов, занимающихся и плаванием, и баскетболом, и легкой атлетикой (п(L)=3). Изобразим описанную ситуацию с помощью кругов Эйлера (Рис.6). Пусть 1 – множество студентов, которые занимаются и плаванием, и баскетболом, и легкой атлетикой;
Чтобы найти число студентов, которые не занимаются ни плаванием, ни баскетболом, ни легкой атлетикой, необходимо из числа всех студентов группы вычесть число студентов, занимающихся хотя бы одним видом спорта, то есть n(А По теореме 3.1 имеем n(А +n(A Так как всего в группе 28 студентов, то не занимаются ни плаванием, ни баскетболом, ни легкой атлетикой: 28–26=2 (студента). Ответ: 2 студента. |
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1455. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ………………………………………………...58
………………………………………………...58 Рис. 1
Рис. 1 Рис.2
Рис.2 .
. . Это было первой формулой, где каждый следующий член последовательности выражался через два предыдущих. Подобные формулы получили название рекуррентных (от лат. recurrere – возвращаться). Метод рекуррентных формул оказался впоследствии полезен для решения комбинаторных задач.
. Это было первой формулой, где каждый следующий член последовательности выражался через два предыдущих. Подобные формулы получили название рекуррентных (от лат. recurrere – возвращаться). Метод рекуррентных формул оказался впоследствии полезен для решения комбинаторных задач. элементов по
элементов по  , выводились выражения для степенных сумм и т. д.
, выводились выражения для степенных сумм и т. д. обозначает, что a есть элемент A, или а принадлежит А, а запись
обозначает, что a есть элемент A, или а принадлежит А, а запись 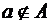 – a не является элементом множества A, или а не принадлежит множеству А.
– a не является элементом множества A, или а не принадлежит множеству А. или
или  .
.  содержит множество В.
содержит множество В. , то
, то  .
. не совпадают. Тогда без ограничения общности можно считать, что существует элемент
не совпадают. Тогда без ограничения общности можно считать, что существует элемент  из множества
из множества  .
.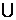 B.
B. , A
, A  …A
…A 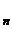 – некоторые множества, то A
– некоторые множества, то A  является множеством, состоящим из всех тех и только тех элементов, которые входят хотя бы в одно из множеств A
является множеством, состоящим из всех тех и только тех элементов, которые входят хотя бы в одно из множеств A  справедливы равенства:
справедливы равенства: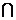 B.
B. Рис.3
Рис.3 Рис.4
Рис.4 (A
(A 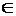 (A
(A  и
и 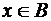 , или
, или  . Отсюда, по дистрибутивному закону конъюнкции относительно дизъюнкции, получаем, что
. Отсюда, по дистрибутивному закону конъюнкции относительно дизъюнкции, получаем, что 



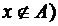 . Отсюда
. Отсюда 
 )=a
)=a  ), A
), A  =Æ, i¹j (i,j=
=Æ, i¹j (i,j= 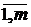 ) Þ n(
) Þ n(  A
A  ) =
) =  a
a  .
. (x
(x  A). Отсюда, по дистрибутивности дизъюнкции относительно конъюнкции, имеем ( x
A). Отсюда, по дистрибутивности дизъюнкции относительно конъюнкции, имеем ( x 
 Из условия также следует, что B
Из условия также следует, что B  Изобразим описанную ситуацию с помощью кругов Эйлера (Рис.5).
Изобразим описанную ситуацию с помощью кругов Эйлера (Рис.5). Рис.5
Рис.5 Рис.6
Рис.6