
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Односторонние реакции третьего порядкаСитуация одного вещества или разных веществ одинаковой концентрации Уравнение реакции: Кинетическое уравнение:
Константа скорости третьего порядка имеет размерность (время)‑1 × (концентрация)‑2. Соответственно, выражение для времени полупревращения:
Уравнение времени полупревращения для реакций n порядка:
Двусторонние (обратимые) реакции Двусторонние реакции первого порядка состоят из прямой и обратной элементарных реакций первого порядка:
Материальный баланс этой реакции:
Здесь следует учесть принцип детального равновесия: в состоянии равновесия любая элементарная стадия протекает с одинаковой скоростью как в прямом, так и в обратном направлении. Общая скорость протекания процесса будет определяться разностью скоростей прямой и обратной реакций.
В приближении первого порядка реакции:
Дифференциальное уравнение общей скорости процесса через пробег реакции:
После интегрирования получаем
где K ‒ константа равновесия реакции; Решая полученную систему получим:
Последовательные реакции Рассмотрим реакцию, состоящую из двух последовательных стадий первого порядка:
Для вывода уравнений зависимости степени превращения веществ от времени потребуется составить материальный баланс:
Скорость первой реакции (считая ее протекающей по первому порядку): 
Скорость образования продукта реакции:
Решение этого дифференциального уравнения дает:
т.е. на кинетической кривой
Времени tmax отвечает максимальная концентрация промежуточного вещества В:
При при при Уравнения для констант скоростей реакций отвечают стандартным уравнениям первого порядка:
Зависимость скорости реакции от температуры Правило Вант-Гоффа Зависимость скорости гомогенной реакции от температуры приближенно выражается правилом Вант-Гоффа, согласно которому при увеличении температуры на скорость химических реакций возрастает в 2 – 4 раза.
где Уравнение Аррениуса Более точно и теоретически обосновано зависимость константы скорости от температуры выражается уравнением Аррениуса:
где В логарифмической форме уравнение имеет вид:
Связь между энергией активации и температурным коэффициентом
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 500. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||
 или
или 
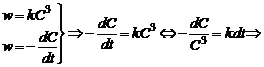


 .
. .
.
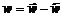
 ;
;
 .
.
 ,
,





 .
.

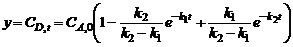 ;
;

 для промежуточного вещества В должен быть максимум. Координаты этого максимума (
для промежуточного вещества В должен быть максимум. Координаты этого максимума (  ) определяются из условия
) определяются из условия  .
. ,
,

 ,
, 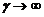 , т.е. медленной первой стадии
, т.е. медленной первой стадии  ;
; ,
,  , т.е. медленной второй стадии
, т.е. медленной второй стадии  ;
; ,
,  .
.
 .
.
 и
и  – константы скорости при температурах
– константы скорости при температурах  и
и  соответственно;
соответственно;  ‑ температурный коэффициент скорости реакции (коэффициент Вант-Гоффа), который обычно изменяется в пределах 2¸4.
‑ температурный коэффициент скорости реакции (коэффициент Вант-Гоффа), который обычно изменяется в пределах 2¸4.
 ‒ энергия активации, A - постоянная (предэкспоненциальный множитель).
‒ энергия активации, A - постоянная (предэкспоненциальный множитель).
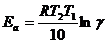 .
.