
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧПО ТЕОРИИ РЯДОВ Задача 37.Найти область сходимости степенного ряда Решение. Данный степенной ряд можно записать так:
Применяем признак Даламбера:
Как видно, ряд будет сходиться для тех значений х, для которых
Выясним вопрос о сходимости ряда на концах интервала. При
Ряд (2) является знакочередующимся; его общий член по абсолютному значению стремиться к нулю при n®¥. По признаку Лейбница о сходимости знакочередующихся рядов заключаем, что ряд (2) сходится. Следовательно, значение х=-2/3 принадлежит области сходимости данного ряда. Подставив в (1) х=2/3, получим
Ряд (3) расходится (для этого достаточно сравнить его с гармоническим рядом). Следовательно, значение х=2/3 не принадлежит области сходимости данного ряда. Таким образом,
Задача 38.Вычислить интеграл Решение. Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд функции sinx, будем иметь
Тогда
Мы получили знакочередующийся ряд, который удовлетворяет условиям теоремы Лейбница. Так как в полученном ряде четвертый член по абсолютному значению меньше 0,0001, то ограничиваемся только первыми тремя членами. Итак,
Задача 39.Разложить в ряд Фурье периодическую функцию f(x), заданную на интервале – периоде (-p,p):
Решение. Заданная функция f(x) удовлетворяет условиям разложения в ряд Фурье, поэтому имеем равенство
 где an и bn определяются по формулам
Положив в (2) n=0, получим коэффициент а0:
Используя формулу (2) и заданную функцию, имеем
Интегрируя по частям, получаем
Определим коэффициенты bn:
Интегрируя по частям, получаем
Подставляя найденные значения коэффициентов Фурье в (1), получаем
Задача 40. Функцию Решение.Так как по условию ряд заданной функции должен содержать только косинусы кратных дуг, то продолжим функцию в интервале (-p;0) четным образом. В результате будет получена четная функция, которая совпадает с заданной на интервале (0;p). Известно, что ряд Фурье для четной функции имеет вид
где
При n=0 получаем:
Интегрируем по частям:
Подставив найденные значения коэффициента Фурье в (1), получим
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Задача 41.Найдите общее решение уравнения 2хуdx+(y2-x2)dy=0. Решение.Данное уравнение является однородным, так как коэффициенты при dx и dy суть однородные функции одного и того же измерения (второго) относительно переменных х и у. Применяем подстановку у=хt, где t – некоторая функция аргумента х. Если у=хt, то дифференциал dy=d(xt)=tdx+xdt, и данное уравнение примет вид
Сократив на х2, будем иметь:
Мы получили уравнение с разделенными переменными относительно х и t. Интегрируя, находим общее решение этого уравнения:
Потенцируя, находим
Задача 42.Найти общее решение уравнения Решение. Данное уравнение является линейным, так как оно содержит искомую функцию у и ее производную у’ в первой степени и не содержит их произведений. Применяем подстановку у=uv, где u и v – некоторые неизвестные функции аргумента х. Если у=uv, то y’=(uv)’=u’v+uv’ и данное уравнение примет вид
или
Так как искомая функция у представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию u так, чтобы выражение, стоящее в круглых скобках левой части равенства (1), обращалось в нуль, т.е. выберем функцию u так, чтобы имело место равенство
При таком выборе функции u уравнение (1) примет вид
Уравнение (2) есть уравнение с разделяющимися переменными относительно u и х. Решим это уравнение:
(Чтобы равенство(2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной С=0). Подставив в (3) найденное выражение для u, получим:
Задача 43.Дано уравнение: Решение. Данное дифференциальное уравнение второго порядка не содержит явно функцию у. Положим у’=р, где р – некоторая функция аргумента х. Если у’=р, то
Определим численное значение С1 при указанных начальных условиях. Имеем 3=С1(0+1). Следовательно, С1=3. Теперь решаем уравнение первого порядка
Определим численное значение С2 при указанных начальных условиях. Имеем 1=0+0+С2; С2=1. Таким образом,
Задача 44. Дано уравнение Решение.Данное уравнение второго порядка не содержит явно аргумента х. Положим у’=р, где р – некоторая функция переменной у. Если у’=р, то
Если приравнять нулю первый множитель, то получаем: р=0; у’=0; у=С – решение данного уравнения. Приравняем нулю второй множитель:
Используя начальные условия, находим С1:
Далее решаем уравнение
Теперь определим значение С2:
Тогда
- искомое частное решение, удовлетворяющее указанным начальным условиям.
Задача 45.Решить систему уравнений и выделить частные решения, удовлетворяющие заданным начальным условиям:
Решение. Обе части первого уравнения системы продифференцируем по переменной t:
В полученном уравнении заменим
Составим и решим соответствующее однородное линейное уравнение:
Характеристическое уравнение k2-k-6=0 имеет корни: k1=-2, k2=3. Следовательно, общее решение (2) имеет вид
Находим частное решение х=Аt+В. Дважды дифференцируя, получим (х)'=А, (х)’’=0. Подставив в (1), находим А=-3 и В=0. Следовательно, х=-3t и
Из первого уравнения системы находим, что
Подставив начальные условия в (3) и (4), получим систему С1+С2=1 и 3С1-2С2=3. Решение этой системы дает С1=1 и С2=0. Следовательно,
- частные решения, удовлетворяющие заданным начальным условиям.
Задача 46.Найти первые три (отличные от нуля) члена разложения в ряд Маклорена функции у(х), являющиеся частным решением дифференциального уравнения у’=х+х2-у2+сosх, если у(0)=1. Решение. Положим, что у(х) является решением данного дифференциального уравнения при указанных начальных условиях. Если у(х) допускает разложение в ряд Маклорена, то имеем
Свободный член разложения (1), т.е. у(0), дан по условию. Чтобы найти значения y'(0), y’’(0), y’’’(0),…, можно данное уравнение последовательно дифференцировать по переменной х и затем вычислить значения производных при х=0. Значение у’(0) получаем, подставив начальные условия в данное уравнение:
Подставив найденные значения производных при х=0 в (1), получим разложение искомого частного решения заданного уравнения:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 243. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 (1)
(1)

 ряд (1) примет вид
ряд (1) примет вид (2)
(2) (3)
(3) - область сходимости исследуемого ряда.
- область сходимости исследуемого ряда. с точностью до 0,0001.
с точностью до 0,0001.



 (1)
(1)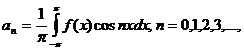 (2)
(2) (3)
(3)




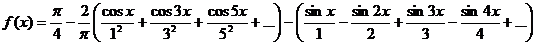
 в интервале (0;p) разложить в ряд косинусов.
в интервале (0;p) разложить в ряд косинусов. (1)
(1) (2)
(2)


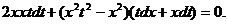


 , или
, или  . Из введенной подстановки следует, что
. Из введенной подстановки следует, что  . Следовательно,
. Следовательно,  или
или  - общее решение данного уравнения.
- общее решение данного уравнения. .
.
 (1)
(1) (2)
(2) (3)
(3)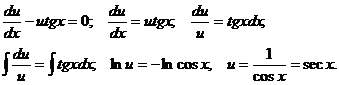
 . Интегрируя, получаем
. Интегрируя, получаем  . Тогда
. Тогда  - общее решение данного уравнения.
- общее решение данного уравнения. . Найти частное решение, удовлетворяющее начальным условиям: у(0)=1; у’(0)=3.
. Найти частное решение, удовлетворяющее начальным условиям: у(0)=1; у’(0)=3. и данное уравнение примет вид
и данное уравнение примет вид  . Мы получили уравнение первого порядка относительно переменных р и х. Решим это уравнение:
. Мы получили уравнение первого порядка относительно переменных р и х. Решим это уравнение:
 :
:
 есть частное решение, удовлетворяющее указанным начальным условиям.
есть частное решение, удовлетворяющее указанным начальным условиям. . Найти частное решение, удовлетворяющее начальным условиям: у(-1)=4; у’(-1)=1.
. Найти частное решение, удовлетворяющее начальным условиям: у(-1)=4; у’(-1)=1. . Тогда данное уравнение примет вид
. Тогда данное уравнение примет вид


 :
: 




 правой частью второго уравнения системы. В результате получим однородное линейное уравнение второго порядка:
правой частью второго уравнения системы. В результате получим однородное линейное уравнение второго порядка: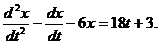 (1)
(1) (2)
(2)
 (3)
(3) , или
, или  , откуда
, откуда (4)
(4)
 (1)
(1)
