
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 27. Обыкновенные дифференциальные уравненияВысших порядков. Дифференциальные уравнения высших порядков. Основные понятия. Уравнения, допускающие понижение порядка. Однородные и неоднородные линейные дифференциальные уравнения. Учебная литература. Основная: 1, 3, 4, 6. Дополнительная: 4, 5, 9, 14, 16, 17. î Контрольная работа №6. Дифференциальные уравнения. Тема 28. Уравнения математической физики.
Физические задачи, приводящие к дифференциальным уравнениям в частных производных. Теплопроводность. Уравнение Лапласа. Формулировка краевых задач. Учебная литература. Основная: 1, 3, 4, 6. Дополнительная: 4, 5, 9, 14, 16, 17.
Раздел 13. Функциональный анализ Тема 29. Элементы функционального анализа
Понятие о линейных пространствах. Линейные функционалы и линейные операторы. Учебная литература. Основная: 3, 6. Дополнительная: 11, 15. Раздел 14. Численные методы и конечные разности Тема 30. Численные методы и конечные разности. Численное решение уравнений. Конечные разности и разностные уравнения. Интерполяция функций. Аппроксимация функций. Численное интегрирование дифференциальных уравнений. Учебная литература. Основная: 3, 4, 6. Дополнительная: 2, 4, 5, 9, 10, 16, 17. Раздел 15. Элементы теории вероятностей, случайных процессов и математической статистики Тема 31. Комбинаторика. Случайные события. Вероятность Случайного события. Элементы комбинаторики. Определение и представление вероятностных моделей. Понятие случайного события. Вероятность случайного события. Аксиоматический подход к определению вероятности. Геометрические вероятности. Произведение и сумма событий, теоремы сложения и умножения вероятностей. Формулы полной вероятности и Байеса. Повторение испытаний, схема Бернулли. Локальная и интегральная теоремы Лапласа.  Учебная литература. Основная: 2, 3. Дополнительная: 6, 7, 8, 12.
Тема 32. Случайные величины, одномерные и многомерные распределения вероятностей. Понятие случайной величины, дискретные и непрерывные случайные величины. Функция и плотность распределения. Числовые характеристики случайных величин. Одномерные и многомерные распределения вероятностей. Функции от случайных величин. Замена переменных. Сходимость по вероятности и предельные теоремы. Специальные методы решения вероятностных задач. Специальные распределения вероятностей. Учебная литература. Основная: 2, 3. Дополнительная: 6, 7, 8, 12. î Контрольная работа №7.Вероятность и законы распределения.
Тема 33. Элементы теории случайных процессов Стационарные случайные процессы. Корреляционные функции и спектральные плотности. Типы случайных процессов. Действия над случайными процессами. Учебная литература. Основная: 2, 3. Дополнительная: 6, 7, 8, 12.
Тема 34. Математическая статистика Статистические методы, статистическое описание, определение и вычисление статистик случайной выборки, типовые распределения вероятностей, оценки параметров, выборочные распределения, проверка статистических гипотез, некоторые статистики, выборочные распределения и критерии для многомерных распределений, статистика и измерения случайного процесса. Учебная литература. Основная: 2, 3. Дополнительная: 6, 7, 8, 12. î Контрольная работа №8. Математическая статистика.
Тема 35. Элементы теории массового обслуживания Основы теории массового обслуживания. Формулировка прикладных задач экозащиты, безопасности и риска. Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска. Моделирование оперативной деятельности подразделений МЧС как системы массового обслуживания. Учебная литература. Основная: 2, 3. Дополнительная: 6, 7, 8, 12. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ ПО АЛГЕБРЕ И ГЕОМЕТРИИ
Задача 1. Данную систему записать в матричной форме и решить с помощью обратной матрицы:
Решение. Пусть А – матрица коэффициентов при неизвестных; Х – матрица-столбец неизвестных х1, х2, х3 и Н – матрица-столбец из свободных членов:
Левую часть системы (1) можно записать в виде произведения матриц А.Х, а правую – в виде матрицы Н. Следовательно, имеем матричное уравнение А.Х=Н. (2) Если определитель матрицы А отличен от нуля, то матрица А имеет обратную матрицу А-1. Умножим обе части равенства (2) слева на матрицу А-1, получим А-1.А.Х=А-1.Н. Так как А-1.А=Е, где Е – единичная матрица, а Е.Н=Х, то Х= А-1.Н. (3) Формулу (3) называют матричной записью решения системы линейных уравнений. Чтобы воспользоваться формулой (3), необходимо сначала найти обратную матрицу А-1: определитель
Заменив (3) соответствующими матрицами, имеем
Откуда х1=2, х2=4, х3=-1.
Задача 2. Решить методом Гаусса следующую систему линейных уравнений:
Решение. Исключим из последних двух уравнений х1. Для этого умножим первое уравнение на -5 и результаты прибавим соответственно ко второму уравнению, затем обе части первого уравнения умножим на -3 и результаты прибавим к третьему уравнению. В результате получим систему эквивалентную данной:
Разделив обе части второго уравнения системы (1) на 2 получим систему
Теперь исключим из третьего уравнения системы (2) х2. Для этого обе части второго уравнения этой системы умножим на -7 и результаты прибавим к третьему уравнению. В результате получим систему
Откуда х3=3, х2=1 и х1=-2. Приведение данной системы к ступенчатому виду (3) практически более удобно, если использовать преобразования расширенной матрицы данной системы, т.е. матрицы, составленной из коэффициентов при неизвестных и свободных членов. Для удобства столбец свободных членов этой матрицы отделим вертикальной чертой. Расширенная матрица данной системы имеет вид
Умножим элементы первой строки матрицы на -5 и результаты прибавим к элементам второй строки, затем умножим элементы первой строки на -3 и результаты прибавим к элементам третьей строки. Получим матрицу
Разделив элементы второй строки на 2, получим
Элементы второй строки умножим на -7 и результаты прибавим к элементам третьей строки. Получим матрицу
которая позволяет данную систему привести к виду (3) и затем решить ее.
Задача 3.Решить методом Гаусса систему уравнений
Решение. Составим расширенную матрицу системы:
Умножив элементы первой строки последовательно на -2, -4 и -5. Полученные результаты прибавим соответственно к элементам второй, третьей и четвертой строк. Получим матрицу
Элементы второй строки умножим на 6 и результаты прибавим к элементам третьей строки, затем элементы второй строки прибавим к элементам четвертой строки. Получим матрицу
Элементы третьей строки разделим на -2 и затем элементы четвертой строки прибавим к элементам третьей строки. Получим матрицу
Теперь элементы третьей строки умножим на 13 и результаты прибавим к элементам четвертой строки. Получим матрицу
Следовательно, данную систему можно записать так:
Откуда х4=0, х3=2, х2=-1 и х1=3. Матрицы, получаемые после соответствующих преобразований, являются эквивалентными. Их принято соединять знаком ~.
Задача 4.Исследовать систему уравнений и решить ее, если она совместна:
Решение. Пусть А – матрица, составленная из коэффициентов при неизвестных. Она называется матрицей системы. Если к матрице а присоединить столбец свободных членов, то полученная матрица В называется расширенной матрицей системы. При исследовании систем линейных уравнений пользуются теоремой Кронекера-Капелли: для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы. При этом если ранг матрицы А равен рангу матрицы В и равен числу неизвестных, то система имеет единственное решение. Если же ранг матрицы А равен рангу матрицы В, но меньше числа неизвестных, то система имеет бесконечное число решений. Если ранг матрицы А меньше ранга матрицы В, то система несовместна и решения не существует. Определим ранг матрицы системы:
Преобразуем матрицу А. Сумму элементов первых двух столбцов прибавим к соответствующим элементам третьего столбца:
Так как все элементы третьего столбца оказались равными нулю, то единственный минор третьего порядка, который имеет эта матрица, равен нулю. С другой стороны минор второго порядка
Преобразуем матрицу В. Сумму элементов первых двух столбцов прибавим к соответствующим элементам третьего столбца. Тогда все элементы третьего столбца будут равны нулю. Затем элементы первого столбца умножим на 2 и их сумму вычтем из соответствующих элементов четвертого столбца:
Так как в полученной матрице, которая эквивалентна расширенной матрице В, элементы двух последних столбцов равны нулю, то все миноры третьего порядка матрицы В равны нулю и, следовательно, ранг матрицы В не может быть равен трем. Таким образом, ранг матрицы В тоже равен 2, т.е. r(В)=2. Итак, r(A)=r(В)=2, но заданная система содержит 3 неизвестных. Поэтому система имеет бесконечное число решений. Выбираем в качестве базисного минора
Решая последнюю систему относительно базисных неизвестных х1 и х2, находим х1=3+х3, х2=2+х3. Полученное решение называется общим. Если свободное неизвестное х3 примет определенное значение, то можно найти соответствующие значения базисных неизвестных х1 и х2. Например, пусть х3=-2, тогда х1=1, х2=0. Легко проверить, что эти решения удовлетворяют всем трем уравнениям заданной системы уравнений. Задача 5.Даны координаты вершин треугольника АВС: А (4; 3), В (16; -6), С (20; 16). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты СD и ее длину; 5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой CD; 6)уравнение прямой, проходящей через точку К параллельно стороне АВ; 7) координаты точки М, расположенной симметрично точке А относительно прямой CD. Решение. 1. Расстояние d между точками A (x1; y1) и B (x2; y2) определяется по формуле
Применяя (1), находим длину стороны АВ:
2. Уравнение прямой проходящей через точки А (x1; y1) и B (x2; y2), имеет вид
Подставляя в (2) координаты точек А и В, получим уравнение стороны АВ:
Решив последнее уравнение относительно y, находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:
Подставив в (2) координаты точек В и С, получим уравнение прямой ВС:
3. Известно, что тангенс угла j между двумя прямыми, угловые коэффициенты, которых соответственно равны k1 и k2, вычисляется по формуле
Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых найдены: kAB=-¾; kВС=5,5. Применяя (3), получим
4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид
Высота CD перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты CD, воспользуемся условием перпендикулярности прямых. Так как kAB=-¾, то kCD=
Чтобы найти длину высоты UD, определим сперва координаты точки D – точки пересечения прямых АВ и CD. Решая совместно систему
находим По формуле (1) находим длину высоты CD:
5. Чтобы найти уравнение медианы АЕ, определим сначала координаты точки Е, которая является серединой стороны ВС, применяя формулы деления отрезка на две равные части:
Следовательно,
Подставив в (2) координаты точек А и Е, находим уравнение медианы:
Чтобы найти координаты точки пересечения высоты CD и медианы АЕ, решим совместно систему уравнений
6. Так как искомая прямая параллельная стороне АВ, то ее угловой коэффициент будет равен угловому коэффициенту прямой АВ. Подставив в (4) координаты найденной точки К и угловой коэффициент k=-¾, получим
Рис. 1. Рис. 2
7. Так как прямая АВ перпендикулярна прямой CD, то искомая точка М, расположенная симметрично точке А относительно прямой CD, лежит на прямой АВ. Кроме того, точка D является серединой отрезка АМ. Применяя формулы (5), находим координаты искомой точки М:
Треугольник АВС, высота CD, медиана АЕ, прямая KF и точка М построены в системе координат хОy на рис. 1.
Задача 6.Составить уравнение геометрического места точек, отношение расстояний которых до данной точки А (4;0) и до данной прямой х=1 равно 2. Решение. В системе координат xOy построим точку А (4;0) и прямую х=1. Пусть М (x;y) – произвольная точка искомого геометрического места точек. Опустим перпендикуляр МВ на данную прямую х=1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно В (1;y) (рис. 2). По условию задачи МА:МВ=2. Расстояния МА и МВ находим по формуле (1) задачи 1:
Возведя в квадрат левую и правую части, получим
Полученное уравнение представляет собой гиперболу, у которой действительная полуось а=2, а мнимая Определим фокусы гиперболы. Дли гиперболы выполняется равенство Определим эксцентриситет полученной гиперболы:
Уравнения асимптот гиперболы имеют вид
Задача 7.Составить уравнение геометрического места точек, равноудаленных от точки А (4;3) и прямой y=1. Полученное уравнение привести к простейшему виду. Решение. Пусть М (х;у) – одна из точек искомого геометрического места точек. Опустим из точки М перпендикуляр МВ на данную прямую у=1 (рис. 3). Определяем координаты точки В. Очевидно, абсцисса точки В равна абсциссе точки М, а ордината точки В равна 1, т.е. В (х;1). По условию задачи МА=МВ. Следовательно, для любой точки М (х;у), принадлежащей искомому геометрическому месту точек, справедливо равенство:
или
Полученное уравнение определяет параболу с вершиной в точке О’ (4;2). Чтобы уравнение параболы привести к простейшему виду, положим х-4=Х и у+2=Y; тогда уравнение параболы принимает вид: Y= ¼Х2(*). Чтобы построить найденную кривую перенесем начало координат в точку О’ (4;2), построим новую систему координат ХО’Y оси которой соответственно параллельны осям Ох и Оy, и затем в этой новой системе построим параболу (*) (рис. 3).
Рис. 3. Рис. 4
Задача 8.Составить каноническое уравнение гиперболы, фокусы которой расположены на оси абсцисс, если она проходит через точки А (-8;12), В (12; Решение. Каноническое уравнение гиперболы имеет вид
По условию точки А и В лежат на гиперболе. Следовательно, координаты этих точек удовлетворяют уравнению (1). Подставив в уравнение (1) вместо текущих координат х и у координаты точек А и В, получим систему двух уравнений относительно неизвестных а и b:
Решая систему, получаем: а2=16, b2=48. Таким образом, уравнение искомой гиперболы Уравнение окружности, проходящей через начало координат, имеет вид
где R – радиус окружности. Так как по условию окружность проходит через фокусы гиперболы, то R=c=8. Следовательно,
В результате получим 4 точки пересечения: М1 (
Задача 9.Даны координаты вершин пирамиды АВСD: А (2;1;0), В (3;-1;2), С (13;3;10), D (0;1;4). Требуется: 1) записать векторы Решение. 1. Произвольный вектор а может быть представлен в системе орт i, j, k следующей формулой:
где ах, ау, аz – проекции вектора а на координатные оси Ох, Оу и Оz, а i, j, и k – единичные векторы, направления которых совпадают с положительным направлением осей Ох, Оу и Оz. Если даны точки М1 (х1;у1;z1) и М2 (х2;у2;z2), то проекции вектора
Тогда
Подставив в (3) координаты точек А и В, получим вектор
Аналогично, подставляя в (3) координаты точек А и С, находим
Подставив в (3) координаты точек А и D, находим вектор
Если вектор а задан формулой (1), то его модуль вычисляется по формуле
Применяя (4), получим модули найденных векторов:
2. Косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей. Находим скалярное произведение векторов
Модули этих векторов уже найдены:
3. Проекция вектора
Площадь грани АВС равна половине площади параллелограмма, построенного на векторах
5. Объем параллелепипеда, построенного на трех некомпланарных вектора, равен абсолютной величине их смешанного произведения. Вычислим смешанное произведение
Следовательно, объем параллелепипеда равен 144 куб. ед., а объем заданной пирамиды АВСD равен 24 куб. ед.
Задача 10.Даны координаты четырех точек: А (0;-2;-1), В (2;4;-2), С (3;2;0) и М (-11;8;10). Требуется: 1) составить уравнение плоскости Q, проходящей через точки А, В и С; 2) составить канонические уравнения прямой, проходящий через точку М перпендикулярно плоскости Q и с координатными плоскостями хОу, хОz и уОz; 4) найти расстояние от точки М до плоскости Q. Решение. 1. Уравнение плоскости, проходящей через три данные точки А (х1;у1;z1), В (х2;у2;z2), С (х3;у3z3), имеет вид
Подставляя в (1) координаты точек А, В и С, получим:
Разложим определитель по элементам первой строки:
Сократив на 5, получим уравнение искомой плоскости Q:
2. Канонические уравнения прямой в пространстве имеют вид
где х0, у0, z0 – координаты точки, через которую проходит прямая (3), а m, n, p – направляющие коэффициенты этой прямой. По условию прямая проходит через точку М (-11;8;10) и перпендикулярна плоскости Q. Следовательно, подставив в (3) координаты точки М и заменив числа m, n и p соответственно числами 2;-1;-2 [коэффициенты общего уравнения плоскости (2)], получим
3. Чтобы найти точки пересечения прямой (4) с плоскостью (2), запишем сначала уравнения прямой (4) в параметрическом виде. Пусть
Подставляя (5) в (2), получим значение параметра t:
Подставив в (5) t=6, находим координаты точки Р пересечения прямой (4) с плоскостью (2):
Пусть Р1 – точка пересечения прямой (4) с координатной плоскостью хОу; уравнение этой плоскости z=0. При z=0 из (5) получаем
Пусть Р2 – точка пересечения прямой (4) с плоскостью хОz; получаем уравнение этой плоскости у=0. При у=0 из (5) получаем
Пусть Р3 – точка пересечения прямой (4) с плоскостью уОz. Уравнение этой плоскости х=0. При х=0 из (5) получаем
4. Так как точка М лежит на прямой (4), которая перпендикулярна плоскости Q и пересекается с ней в точке Р, то для нахождения расстояния от точки М до плоскости Q достаточно найти расстояние между точками М и Р:
Задача 11.Даны координаты трех точек: А (-5;2;-2), В (-1;4;-6), С (-4;1;-6). Требуется найти: 1) канонические уравнения прямой АВ; 2) уравнение плоскости, проходящей через точку С перпендикулярно прямой АВ и точку пересечения этой плоскости с прямой АВ; 3) расстояние от точки С до прямой АВ. Решение. 1. Уравнения прямой, проходящей через две данные точки А (х1;у1;z1) и В (х2;у2;z2), имеют вид
Подставив в (1) координаты точек А и В, получим
2. Запишем уравнение плоскости в общем виде Ах+Ву+Сz+D=0. Если плоскость проходит через точку М (х0;у0; z0), то уравнение пучка плоскостей имеет вид
Так как искомая плоскость перпендикулярна прямой АВ, то А:В:С=2:1:-2. Заменив коэффициенты А, В, С, в уравнении пучка плоскостей соответственно числами 2, 1, -2 и подставляя координаты точки С (-4;1;-6), получим
Определим координаты точки пересечения плоскости (q) с прямой АВ. Для этого решим систему трех уравнений
Решая эту систему, находим х=-3, у=3, z=-4. Следовательно, плоскость и прямая пересекаются в точке Р (-3;3;-4). 3. Чтобы найти расстояние от точки С до прямой АВ, достаточно найти расстояние от точки С (-4;1;-6) до пересечения Р(-3;3;-4) (так как прямая перпендикулярна плоскости q). Имеем
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 238. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1)



 (1)
(1) (2)
(2) (3)
(3)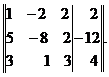
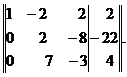




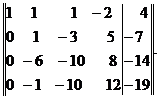






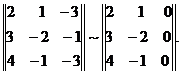
 . Следовательно, ранг матрицы А равен 2, т.е. r(A)=2. Определим теперь ранг расширенной матрицы В:
. Следовательно, ранг матрицы А равен 2, т.е. r(A)=2. Определим теперь ранг расширенной матрицы В:

 , а в качестве базисных неизвестных х1 и х2. Составляем подсистему, состоящую из первых двух уравнений заданной системы (третье уравнение отбрасываем). Свободное неизвестное х3 переносим в правую часть. Получаем
, а в качестве базисных неизвестных х1 и х2. Составляем подсистему, состоящую из первых двух уравнений заданной системы (третье уравнение отбрасываем). Свободное неизвестное х3 переносим в правую часть. Получаем
 (1)
(1)
 (2)
(2)


 (3)
(3)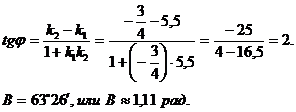
 (4)
(4) . Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим
. Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим



 (5)
(5)







 .
. . Следовательно,
. Следовательно,  – фокусы гиперболы. Как видно, заданная точка А (4;0) является правым фокусом гиперболы.
– фокусы гиперболы. Как видно, заданная точка А (4;0) является правым фокусом гиперболы.
 и
и  . Следовательно,
. Следовательно,  , или
, или  и
и  – асимптоты гиперболы. Прежде чем построить гиперболу, строим ее асимптоты.
– асимптоты гиперболы. Прежде чем построить гиперболу, строим ее асимптоты.


 ). Найти все точки пересечения этой гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы.
). Найти все точки пересечения этой гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы.

 . Определим фокусы этой гиперболы. Имеем с2=а2+b2=16+48=64; с=8; F1 (-8;0), F2 (8;0).
. Определим фокусы этой гиперболы. Имеем с2=а2+b2=16+48=64; с=8; F1 (-8;0), F2 (8;0).
 - уравнение окружности. Чтобы найти точки пересечения гиперболы с окружностью, решим систему уравнений
- уравнение окружности. Чтобы найти точки пересечения гиперболы с окружностью, решим систему уравнений
 ;6), М2 (-
;6), М2 (-  в системе орт i, j, k и найти модули этих векторов; 2) найти угол между векторами
в системе орт i, j, k и найти модули этих векторов; 2) найти угол между векторами 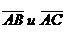 ; 3) найти проекцию вектора
; 3) найти проекцию вектора 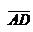 на вектор
на вектор  ; 4) найти площадь грани АВС; 5) найти объем пирамиды АВСD.
; 4) найти площадь грани АВС; 5) найти объем пирамиды АВСD. (1)
(1) на координатные оси находятся по формулам:
на координатные оси находятся по формулам: (2)
(2) (3)
(3)
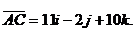

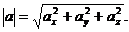 (4)
(4)
 :
:
 . Следовательно,
. Следовательно,
 на вектор
на вектор 

 :
: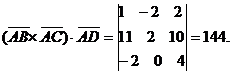
 (1)
(1)

 (2)
(2)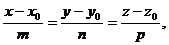 (3)
(3) (4)
(4) , где t – некоторый параметр. Тогда уравнения прямой можно записать так:
, где t – некоторый параметр. Тогда уравнения прямой можно записать так: (5)
(5)



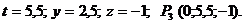

 (1)
(1)



