Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ИСЧИСЛЕНИЮ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХЗадача 31.Исследовать на экстремум функцию z=-4+6x-x2-xy-y2. Решение.Чтобы исследовать данную дважды дифференцируемую функцию z=f(x,y) на экстремум, необходимо: 1. Найти частные производные первого порядка
Каждая пара действительных корней этой системы определяет одну стационарную точку исследуемой функции. Пусть Р0 (х0;у0) одна из этих точек. 2. Найти частные производные второго порядка Положим, что 3. Составить и вычислить определитель второго порядка 4. Если в исследуемой стационарной точке Р0 (х0;у0) D>0, то функция z=f(x,y) в этой точке имеет максимум при А<0 и минимум при А>0; если D<0, то в исследуемой точке нет экстремума. Если D=0, то вопрос об экстремуме требует дополнительного исследования. Находим стационарные точки заданной функции:
Решение системы Следовательно, данная функция имеет только одну стационарную точку Р0 (4,-2). Находим частные производные второго порядка и их значения в найденной стационарной точке:
Как видно, частные производные второго порядка не содержат х, они постоянны в любой точке и, в частности в точке Р0 (4,-2). Имеем А=-2; В=-1; С=-2.
Так как D>0 и А<0, то в точке Р0 (4;-2) данная функция имеет максимум:
Задача 32. Написать уравнение касательной плоскости и уравнение нормали к поверхности 3ху2-2уz+4xz-2=0 в точке М0 (х0;у0;z0), если х0=-1 и у0=2. Решение. Определим аппликату z0 точки касания; для этого подставляем значения х0 и у0 в данное уравнение поверхности:
Таким образом, М0 (-1;2;-2) – точка касания. Уравнение касательной плоскости, проведенной к поверхности F (x,y,z)=0 в точке М0 (х0;у0;z0), имеет вид: 
Нормаль проходит через точку касания и перпендикулярная касательной плоскости. Уравнения нормали имеют вид:
Находим частные производные
Подставив в (1) найденные значения частных производных и координаты точки касания, получаем
или после упрощения х-2у-2z+1=0 – уравнение касательной плоскости. Из (2) имеем
или
Задача 33.Найти наибольшее и наименьшее значения функции z=x2+2y2-2x-8y+5 в замкнутом треугольнике АОВ, ограниченном осями координат и прямой х+у-4=0 (рис. 12).
Рис. 12.
Решение. Чтобы найти наибольшее и наименьшее значения функции в заданной замкнутой области, необходимо: 1) найти стационарные точки, лежащие внутри области, и вычислить значения функции в этих точках; исследовать на экстремум эти точки не следует; 2) найти наибольшее и наименьшее значения функции на границе области; если граница состоит из нескольких линий, то исследование проводится для каждого участка в отдельности; 3) сравнить полученные значения функции и установить наибольшее и наименьшее значения функции в заданной замкнутой области. Находим стационарные точки, лежащие внутри заданной области:
Приравняв нулю частные производные и решив полученную систему
находим стационарную точку Р0 (1;2). Эта точка принадлежит заданной области. Вычислим значение функции в этой точке: z(P0)=z(1;2)=1+8-2-16+6=-4. Граница области состоит из отрезка ОА оси Ох, отрезка ОВ оси Оу и отрезка АВ. Определим наибольшее и наименьшее значения функции z на каждом из этих трех участков. На отрезке ОА у=0, а 0£х£4. Если у=0, то z(х)=х2-2х+5. Находим наибольшее и наименьшее значения этой функции на отрезке [0,4]:
Вычислим значения функции на концах отрезка ОА, т.е. в точках 0 (0;0) и А (4;0): z(0)=5; z(4)=13. На отрезке ОВ х=0 и 0£у£4. Если х=0, то z(у)=2у2-8у+5. Находим наибольшее и наименьшее значения этой функции на отрезке [0,4]:
В точке О (0;0) значение функции уже было найдено. Вычислим значение функции в точке В z(B)=z(0;4)=5. Теперь исследуем отрезок АВ. Уравнением прямой АВ будет у=4-х. Подставив это выражение для у в заданную функцию z, получим
Определим наибольшее и наименьшее значения этой функции на отрезке [0,4]:
Р3 – стационарная точка на отрезке АВ. Вычислим значение функции в этой точке:
Значения функции на концах отрезка АВ найдены ранее. Сравнивая полученные значения функции z в стационарной точке Р0 заданной области, в стационарных точках на границах области Р1, Р2, Р3 и в точках О, А, и В, заключаем, что наибольшее значение в заданной замкнутой области функция z имеет в точке А, наименьшее значение – в точке Р0 (1;2). Итак,
Задача 34. Дан интеграл Решение.1. Пределы внешнего интеграла по переменной х – числа 1 и 3 – указывают на то, что область D ограничена слева прямой х=1 и справа прямой х=3. Пределы внутреннего интеграла по переменной у указывают на то, что область D ограничена снизу параболой у=(х-1)2+1 и сверху прямой у=2х-1. Построив эти линии на отрезке [1;3], получим область D (рис. 13).
Рис. 13. Рис. 14: 1 -
2. Чтобы изменить порядок интегрирования, установим пределы интегрирования для внешнего интеграла по переменной у. Как видно из рис 13, наименьшее значение, которое принимает у в области D, равно 1 в точке А (1;1), а наибольшее значение равно 5 в точке В (3;5). Следовательно, внешний интеграл по переменной у будет иметь пределы: 1 (нижний предел) и 5 (верхний предел). Определим пределы для внутреннего интеграла по переменной х. Из уравнения прямой у=2х-1 получаем Из уравнения параболы у=(х-1)2 получаем
3. Вычислим площадь области D при заданном порядке интегрирования:
Вычислим площадь области D при измененном порядке интегрирования:
Задача 35.Найти объем тела, ограниченного параболоидом z=6-x2-y2 и конусом Решение. Искомый объем V находим с помощью
Определим область D. Исключая из заданных уравнений поверхностей z, получим уравнение контура области D:
откуда
Как видно из уравнения (2), область D представляет круг с центром в начале координат и радиусом, равным 2. Чтобы вычислить интеграл (1), перейдем к полярным координатам: х=rcosj и y=rsinj. Область D определяется неравенствами: 0£j£2p, 0£r£2. Выразим подынтегральное выражение (1) через r и j. Заменяя х2+у2 через r2 и dxdy через rdrdj, получим
Задача 36. Найти функцию U (х,у), если ее дифференциал
Решение. Рассмотрим криволинейный интеграл
Так как под знаком криволинейного интеграла имеется полный дифференциал, то этот интеграл не зависит от контура интегрирования. Выберем на плоскости хОу три точки: А (0;0), В (х;0) и М (х;у) и за контур интегрирования К примем ломаную АМВ. На отрезке АВ у=0 и, следовательно, dy=0; на отрезке ВМ х=const и, следовательно, dх=0.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 240. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  , приравнять их нулю и решить систему уравнений
, приравнять их нулю и решить систему уравнений
 и вычислить их значения в каждой стационарной точке.
и вычислить их значения в каждой стационарной точке. .
. .
.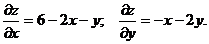
 дает х0=4, у0=-2.
дает х0=4, у0=-2.



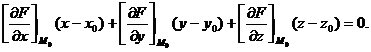 (1)
(1) (2)
(2) и вычисляем их значения в точке касания М0 (-1;2;-2):
и вычисляем их значения в точке касания М0 (-1;2;-2):


 - искомые уравнения нормали.
- искомые уравнения нормали.






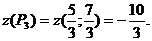

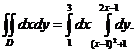 Требуется: 1) построить на плоскости хОу область интегрирования D; 2) изменить порядок интегрирования; 3) вычислить площадь области D при заданном и измененном порядке интегрирования.
Требуется: 1) построить на плоскости хОу область интегрирования D; 2) изменить порядок интегрирования; 3) вычислить площадь области D при заданном и измененном порядке интегрирования.
 ; 2 -
; 2 - 
 нижний предел.
нижний предел. - верхний предел. Таким образом,
- верхний предел. Таким образом,


 (1)
(1)
 (2)
(2)