
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теория множеств.Операции.Семейства.Под множеством S будем понимать любое собрание определенных и различимых между собой объектов, мыслимое как единое целое. Эти объекты называются элементами множества S. Множество А называется подмножеством множества В, если всякий элемент из А является элементом В Множество, не содержащее элементов, называется пустым Ж, оно является подмножеством любого множества. Множество U называется универсальным, то есть все рассматриваемые множества являются его подмножеством. Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств. Операции над множествами: рассматриваются для получения новых множеств из уже существующих. Объединением (рис.1)множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):
Пересечением(рис.2) множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):
Разностью(рис3).множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3): 
Симметрической разностью(рис.4) множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):
Теория графов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара множеств G=(V,E), где V есть подмножество любого счётного множества, а E — подмножество V×V. Графом называется совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрами или дугами графа. Элементы графов: Вершины графа, которые не принадлежат ни одному ребру, называются изолированными. Граф, состоящий только из изолированных вершин, называется нуль -графом. Граф, в котором каждая пара вершин соединена ребром, называется полным. Граф, степени всех k вершин которого одинаковы, называется однородным графом степени k. Граф называется связным, если каждые две его вершины связны; если же в графе найдется хотя бы одна пара несвязных вершин, то граф называется несвязным. Связанный неориентированный ациклический граф называетсядеревом. Множество деревьев называется лесом. Теорема 1. Удвоенная сумма степеней вершин любого графа равна числу его ребер. Теорема 2. Число нечетных вершин любого графа четно. Теорема 3. Во всяком графе с n вершинами, где n больше или равно 2, всегда найдутся две или более вершины с одинаковыми степенями. Теорема 4. Если в графе с n вершинами (n ≥2) только одна пара имеет одинаковую степень, то в этом графе всегда найдется либо единственная изолированная вершина, либо единственная вершина, соединенная со всеми другими. Теорема 5. Если у графа все простые циклы четной длины, то он не содержит ни одного цикла четной длины. Теорема 6. Для того, чтобы граф был эйлеровым, необходимо и достаточно, чтобы он был связным и все его вершины имели четную степень. Теорема 7. Для того чтобы на связном графе можно было бы проложить цепь АВ, содержащую все его ребра в точности по одному разу, необходимо и достаточно, чтобы А и В были единственными нечетными вершинами этого графа. Теорема 8. Полный граф с пятью вершинами не является плоским. Плоские планарные графы. Правильная ориентация графа. Изоморфные графы. Дополнение графа. Полный граф. Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер. Плоский граф — граф уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу. Графы Г1 и Г2 называют изоморфными если в них одинаковое число вершин и вершинам, которые смежны в первом графе можно однозначно сопоставить вершины смежные во втором, то же самое с вершинами не являющимися смежными. Другими словами: изоморфные графы являются реализацией одного и того же графа, полученного переменною места положения вершин, но с сохранением положения смежности. Дополнение графа- это граф с тем же числом вершин, но вершины смежные в исходном графе не смежные в дополнительном и наоборот. Исходный граф и граф являющийся дополнением к нему при совмещении дают полный граф. Замечание. Изоморфным графам соответствуют изоморфные дополнения. Правильный граф-это граф в геометрической реализации которого нет пересечений между ребрами. Ориентированный граф- это граф в котором каждое ребро имеет направление |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 367. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


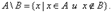




 – вершина;
– вершина;  – ориентированное ребро;
– ориентированное ребро;  – неориентированное ребро;
– неориентированное ребро;  – петля.
– петля.