
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение задач с применением треугольника ПаскаляРассмотрим одну из задач Ферма, решенную Паскалем с помощью своей числовой таблицы. Пусть до выигрыша всей встречи игроку А недостает двух партий, а игроку В - трех партий. Как справедливо разделить ставку, если игра прервана? Паскаль складывает количество партий, недостающих игрокам, и берет строку таблицы, в которой количество членов равно найденной сумме, т.е. 5. Тогда доля игрока А будет равна сумме трех (по количеству партий, недостающих игроку В) первых членов пятой строки, а доля игрока В - сумме оставшихся двух чисел. Выпишем эту строку: 1,4,6,4, 1. Доля игрока А равна 1+4+6=11, а доля В -1+4=5. Замкнутые классы. Полнота. Пусть мн-во Мн-во М называется замкнутым, если его замыкание совпадает с самим мн-ом, т.е. |M|={0,1}=M. Мн-во М называется полным, если его замыкание совпадает с множеством Свойства:1. 2. 3. Теорема. Пусть 1)Если 2)Если
Классы Поста Lи S 3.Класс L .Пусть
Мн-во всех линейных функций
Теорема.Мн-во функций во мн-ве Теорема. Класс Лемма. Из произвольной нелинейной ф-ии с помощью подстановки констант и отрицаний можно получить конъюнкцию 2-х переменных.
4.Класс S . Пусть 
Теорема. Класс Теорема. Лемма. Из любой несамодвойственной ф-ии с помощью операции отрицание и отождествление переменных можно получить константы
Класс Поста М. Критерий полноты 5.Класс М .Класс монотонных функций. Введём на мн-ве
Теорема.Б.о. Пусть . Обозначим через Мн-во всех монотонных функций . Теорема. Класс Лемма. Из любой немонотонной ф-ии с помощью подстановки констант и отождествление переменных можно получить отрицание. Критерий полноты (теорема Поста). 1.Для того, чтобы мн-во 2. Для того, чтобы мн-во среди функций из 3. Для того, чтобы мн-во Таблица Поста для
13. Классы Поста Р0 и Р1 и их свойства Классы Поста. 1.Класс Теорема. Число ф-ий во мн-ве
Теорема. Класс Лемма. Если ф-ия 2.Класс Теорема.Число ф-ий во мн-ве
Теорема. Класс Лемма. Если ф-ия 14. Определение тавтологии, противоречия. Опровержимая и выполнимая формулы логики высказываний.Основные тавтологии. 1)Формула Р(х1,х2,…,хn) называется тавталогией,если она принимает знач «1» для любого набора знач вход-хв нее переменных. 2)Формула Р(х1,х2,…,хn) наз-сяпротиворечием,если она принимает знач «0» на всех наборах переменных х1,х2,…,хn. 3)Если дана ФАВ Р(х1,х2,…,хn),то она наз опровержимой в том случае,когдасущ-т такой набор переменных со знач а1,…,аn (an=xn) что Р(а1,а2,…,аn)=0. 4) Формула назвыполнимой,еслисущ такой набор знач-й переменных а1,а2,…,аn, что Р(а1,а2,…,аn)=1. С точки зрения логики высказ-й,тавтология это логич закон. 1)А v(А)=1 2) А→(В→(А))=1 3)(А→В)→((В→С)→(А→С))=1 4)(АВ)→(ВА)=1 (АВ)→В=1 5)А→(В→АВ)=1 6)А→(АvВ)=1 7)(В→А)→((В→А)→В)=1 8)((А→В)→А)→А=1-закон пирса |
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 921. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
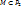 . Замыканием мн-ва М называется мн-во обозначаемое |М|, которое состоит из функций мн-ва М и функций, которые могут быть получены из ф-иймн-ва М путём операции отождествления переменных и конечного числа суперпозиций.
. Замыканием мн-ва М называется мн-во обозначаемое |М|, которое состоит из функций мн-ва М и функций, которые могут быть получены из ф-иймн-ва М путём операции отождествления переменных и конечного числа суперпозиций.



 – часть
– часть  , тогда:
, тогда: . Говорят, что
. Говорят, что  линейна, если её канонический многочлен Жегалкина не содержит произведений переменных. Обозначим через
линейна, если её канонический многочлен Жегалкина не содержит произведений переменных. Обозначим через  мн-во линейных функций от n-переменных.
мн-во линейных функций от n-переменных.
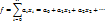
 .
. замкнут и неполон.
замкнут и неполон.
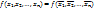 . Обозначим через
. Обозначим через  мн-во самодвойственных функций от n-переменных.
мн-во самодвойственных функций от n-переменных.
 замкнут и неполон.
замкнут и неполон.
 и
и  .
. бинарное отношение
бинарное отношение  определённое след-им:
определённое след-им: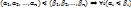
 на
на  порядок частичный.
порядок частичный.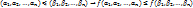
 мн-во всех монотонных функций от n-переменных и через
мн-во всех монотонных функций от n-переменных и через 
 замкнут и неполон.
замкнут и неполон. было полным, необходимо и достаточно, чтобы оно не являлось подмножеством ни одного из множеств классов Поста:
было полным, необходимо и достаточно, чтобы оно не являлось подмножеством ни одного из множеств классов Поста: 
 нашлась функция, не принадлежащая этому классу Поста.
нашлась функция, не принадлежащая этому классу Поста.









 . Пусть
. Пусть  , если
, если  . Обозначим через
. Обозначим через 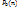 мн-во функций сохраняющих ноль от n-переменных. За
мн-во функций сохраняющих ноль от n-переменных. За 
 или
или  .
. . Пусть
. Пусть  . Обозначим через
. Обозначим через 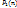 мн-во функций сохраняющих ноль от n-переменных. За
мн-во функций сохраняющих ноль от n-переменных. За 