
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема (крит.тожд.ист-ти формул)Стр 1 из 9Следующая ⇒ Элементарные булевы функции. Конъюнкция, дизъюнкция. Среди булевых функций особо выделяются так называемые элементарные булевы функции, посредством которых можно описать любую булеву функцию от любого числа переменных. 1) Отрицанием(инверсией)называется булева функция одной переменной, которая определяется следующей таблицей истинности:
(Обозначения: x, Свойство: 2) Конъюнкцией(логическое умножение (произведение); логическое «и»)называется булева функция двух переменных, которая определяется следующей таблицей истинности (далее то же самое):
Обозначения: x&y, x⋅y, Свойства: 1) 3)Дизъюнкцией(логическое сложение (сумма); логическое «или») называется … :
Обозначения: Свойства: 1). Импликация, эквиваленция 4) Импликацией(логическое следование) называется … :
Обозначения: x→y, x⇒y.  Свойства: 1) 5) Эквивалентностьюназывается… :
Обозначения: x∼y, x↔y. Свойства: 1) Функция Шеффера, стрелка Пирса, двоичное сложение 6) Cуммой по модулю 2 (Другое название: антиэквивалентность) называется … :
Обозначения: x⊕y, x+y. 7) Штрих Шеффера это … :
Другое название: отрицание конъюнкции, логическое «не-и».
Другое название: отрицание дизъюнкции, логическое «не-или», функция Вебба. Обозначение: x↓y; для функции Вебба - x°y.
Принцип двойственности. Определение (Двойственная функция)Пусть Следствие: Из этой теоремы можно получить закон отрицания: Пример (двойственные функции).
Теорема(Закон двойственности) Формулы При постр. таблиц истинности, двойств. формулу можно получить, используя симметрию и инверсию относительно середины таблицы.
Теорема(Принцип двойственности для булевых формул) Двойственная к булевой формула может быть получена путем замены констант 0 на 1, 1 на 0; дизъюнкцию на конъюнкцию(
Нормальные формы. СДНФ. Пусть
Продолж.анал-ныерассужд.,решением этого ур-я явл.множ. Лемма(о разлож.поперем) Пусть Применим эту лемму. Формулу алг.выск.
(*)-называется полным дизъюнктивным разложением для формулы f. В этой формуле множ-ль Доказано. Теорема Для любой формулы алгебры выск. ≠0 сущ-т ее представление (1), называемое Совершенной Дизъюнктивной Нормальной Формой – СДНФ. Теорема Для любой ≠0 форм.алг.выск., существует единственное ее представление в виде СДНФ. Теорема (крит.тожд.ист-ти формул) Для того чтобы форм.алг.выск. была =0, необх и дост, чтобы в равносильной ей ДНФ, все элементы конъюнкции были ложны. Нормальные формы. СКНФ. Теорема.Для любой отличной от тождественно ложной формулы алгебры высказываний существует единственное представление её в виде СКНФ.
Теорема. (Критерий тождественной истинности формул) Для того, чтобы ф.а.в. была тождественно истинной ,необходимо и достаточно, чтобы в равносильной ей КНФ были тождественно истинны все элементарные дизъюнкции. Теорема.(Критерий тождественной истинности элементарной дизъюнкции). Для того, чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно, чтобы в ней существовала хотя бы для одной переменной пара – переменная и её отрицание (
K-значная логика. Пусть U={ ОПР.Функцияf
8 Множество P2(n) Бу́левафу́нкция (или логи́ческая функция, или функция а́лгебрыло́гики) от n переменных — в дискретной математике отображение Bn → B, где B = {0,1} — булево множество. Элементы булева множества 1 и 0 обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определенного смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения Bn называют булевыми векторами. Множество всех булевых функций от любого числа переменных часто обозначается P2, а от n переменных — P2(n). Каждая булева функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 2n. Поскольку на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n-арных булевых функций равно 22n. Поэтому в этом разделе рассматриваются только простейшие и важнейшие булевы функции. То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят название таблиц истинности и в общем случае имеют вид: x1x2 … xn f(x1,x2,…,xn) 0 0 … 0 f(0,0,…,0) 00 … 1 f(0,0,…,1) 01 … 0 f(0,1,…,0) 01 … 1 f(0,1,…,1) ………………………………………………………………………………………………. 10 … 0 f(1,0,…,0) 10 … 1 f(1,0,…,1) 11 … 0 f(1,1,…,0) 11 … 1 f(1,1,…,1) Практически все булевы функции малых арностей (0, 1, 2 и 3) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных (то есть строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется фиктивной. Нульарные функции При n = 0 количество булевых функций сводится к двум Унарные функции При n = 1 число булевых функций равно
Бинарные функции При n = 2 число булевых функций равно Таблица значений булевых функций от двух переменных:
Тернарные функции При n = 3 число булевых функций равно
Суперпозиция и замкнутые классы функций
Результат вычисления булевой функции может быть использован в качестве одного из аргументов другой функции. Результат такой операции суперпозиции можно рассматривать как новую булеву функцию со своей таблицей истинности. Например, функции
Говорят, что множество функций замкнуто относительно операции суперпозиции, если любая суперпозиция функций из данного множества тоже входит в это же множество. Замкнутые множества функций называют также замкнутыми классами.
В качестве простейших примеров замкнутых классов булевых функций можно назвать множество {x}, состоящее из одной тождественной функции, или множество {0}, все функции из которого тождественно равны нулю вне зависимости от своих аргументов. Замкнуты также множество функций Разумеется, множество P2 всех возможных булевых функций тоже является замкнутым. 9 Полиномом (многочленом) Жегалкина от п переменных называется функция P = a0 + a1x1 +a2x2 + ...anxn +an +1x1x2 +...+an +C2nxn-1xn + ...+a2n-1x1x2..xn Всего здесь 2n слагаемых. Напомним, что + сейчас означает сложение по модулю 2, коэффициенты a0, a1,..., a2n-1 являются константами (равными нулю или единице). Теорема. Любая функция п переменных может быть представлена полиномом Жегалкина и это представление единственно. Доказательство. Любая функция f(x1, x2, …, xn) имеет свою таблицу истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределенными коэффициентами. Затем по очереди подставляем всевозможные наборы переменных и находим коэффициенты. Легко видеть, что за каждую подстановку находим только один коэффициент. Так как число наборов равно числу коэффициентов (и равно 2n), отсюда следует утверждение теоремы. Доказательство этой теоремы показывает, как по таблице истинности построить полином Жегалкина. Имеется 2-й способ нахождения полинома Жегалкина для функций, заданных в виде ДНФ. Этот способ основан на том, что х+1 = Пример. Последнее выражение и есть полином Жегалкина данной функции. Функция f(x1, x2, …, xn) называется линейной, если ее полином Жегалкина содержит только первые степени слагаемых. Более точно функция называется линейной, если ее можно представить в видеf(x1, x2, …, xn) = a0 + a1x1 + a2x2 +…+ anxn. Класс линейных функций часто обозначают через L. (Заметим, что число линейных функций п переменных равно 2n+1).
Треугольник Паскаля - это просто бесконечная числовая таблица "треугольной формы", в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа в предшествующей строке. Таблица обладает симметрией относительно оси, проходящей через его вершину.
Свойства треугольника Паскаля Свойства строк Сумма чисел n-й строки Паскаля равна 2 n (потому что при переходе от каждой строки к следующей сумма членов удваивается, а для нулевой строки она равна 20=1) Все строки Паскаля симметричны (потому что при переходе от каждой строки к следующей свойство симметричности сохраняется, а нулевая строка симметрична) Каждый член строки Паскаля с номером n тогда и только тогда делится на т, когда т- простое число, а n - степень этого простого числа Нахождение элемента треугольника Каждое число в треугольнике Паскаля можно определить тремя способами: Оно равно Cnk, где n - номер строки, k- номер элемента в строке Докажем, что оно равно сумме чисел предыдущей диагонали, начиная со стороны треугольника и кончая числом, стоящим над данным (в силу симметричности треугольника Паскаля докажем это утверждение для левой диагонали). Мы должны проверить следующее равенство:
Действительно,
Каждое число треугольника Паскаля, уменьшенное на единицу, равно сумме всех чисел, заполняющих параллелограмм, ограниченный теми правой и левой диагоналями, на пересечении которых стоит данное число, причем сами эти диагонали в рассматриваемый параллелограмм не включаются. Докажем это. Данное число равно сумме чисел предыдущей диагонали, начиная со стороны треугольника и кончая числом, стоящим над ним. В свою очередь, последний член этой суммы равен сумме элементов предыдущей диагонали и т.д. Продолжая этот процесс, придем к сумме чисел требуемого параллелограмма и еще одного члена, стоящего на стороне треугольника и равного 1. Треугольные числа Вдоль диагоналей, параллельных сторонам треугольника, выстроены треугольные, тетраэдрические и другие числа. Треугольные числа указывают количество шаров или других предметов, уложенных в виде треугольника (эти числа образуют следующую последовательность: 1,3,6,10,15,21,..., в которой 1- первое треугольное число, 3- второе треугольное число, 6-третье и т.д. до m-ro, которое показывает, сколько членов треугольника Паскаля содержится в первых m его строках - от нулевой до (m-1)-й). Тетраэдрические числа Члены последовательности 1,4, 10, 20, 36, 56,... называются пирамидальными, или, более точно, тетраэдрическими числами: 1- первое тетраэдрическое число, 4- второе, 10- третье и т.д. до m-ro. Эти числа показывают, сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра). Числа Фибоначчи В 1228 году выдающийся итальянский математик Леонардо из Пизы, более известный сейчас под именем Фибоначчи, написал свою знаменитую "Книгу об абаке". Одна из задач этой книги - задача о размножении кроликов - приводила к последовательности чисел 1,1,2,3,5,8,13,21..., в которой каждый член, начиная с третьего, представляет собой сумму двух предыдущих членов. Эта последовательность носит название ряда Фибоначчи, члены ряда Фибоначчи называют числами Фибоначчи. Обозначая n-е число Фибоначчи через Между рядом Фибоначчи и треугольником Паскаля существует любопытная связь. Образуем для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел. Получим для первой диагонали 1, для второй 1, для третьей 2, для четвертой 3, для пятой 5. Мы получили не что иное, как пять начальных чисел Фибоначчи. Оказывается, что всегда сумма чисел n-й диагонали есть n-е число Фибоначчи. Для доказательства интересующего нас предложения достаточно показать, что сумма всех чисел, составляющих n-ю и (n+1) диоганали треугольника Паскаля равна сумме чисел, составляющих его т+2-ю диагональ. Но на n-й диагонали расположены числа С0n-1, С1n-2, С2n-3, ..., а на n+1-й - числа С0n, С1n-1, С2n-2, ... Сумму всех чисел запишем так: С0n + (С0n-1+ С1n-1) + (С1n-2+ С2n-2) +... или С0n+1 +С1n +С2n-1 +... Последнее выражение есть сумма чисел, лежащих на (n+2)-й восходящей диагонали треугольника. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 435. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 принимающая значение 1 на всех наборах нулей и единиц называется константой 1, или тождественной единицей. Обозначение: 1.
принимающая значение 1 на всех наборах нулей и единиц называется константой 1, или тождественной единицей. Обозначение: 1. . Запись
. Запись 
 Запись читается «икс и игрек» или «икс умножить на игрек».
Запись читается «икс и игрек» или «икс умножить на игрек». , 2)
, 2) 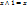 ,
,  , 3)
, 3) 
 ,
,  ,
,  ,
,  , 3)
, 3) 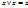
 , 2)
, 2)  ,
,  ,
,  ,
,  ,
, 
 , 2)
, 2) 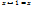 ,
,  3)
3) 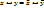
 , опред.след.рав-вом:
, опред.след.рав-вом: 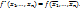

 ;
;  ;
;  ;
; 
 и
и 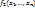 равносильны ó когда равносильны их двойств.формулы, т.е.:
равносильны ó когда равносильны их двойств.формулы, т.е.: 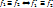 .
.







 ), конъюнкцию на дизъюнкцию(
), конъюнкцию на дизъюнкцию(  );и сохранение структуры формулы, т.е. соотв-го порядка действий.
);и сохранение структуры формулы, т.е. соотв-го порядка действий.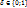 , x – выск.переменная. тогда:
, x – выск.переменная. тогда: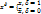 , тогда ур.
, тогда ур. 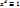 будет иметь ед.реш.
будет иметь ед.реш. 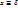 . Рассм.след.ур:
. Рассм.след.ур:  , где
, где  неизв-е,
неизв-е,  – параметр. Решением ур.будет
– параметр. Решением ур.будет  . Рассм:
. Рассм:  ,
, 
 .
.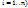 , тогда
, тогда  , ее же можно записать:
, ее же можно записать:  ,
,  ,
,  . Аналогично, применяя лемму:
. Аналогично, применяя лемму:  ,
,  . Применяя закон о дистрибутивности конъюнкции относительно дизъюнкции:
. Применяя закон о дистрибутивности конъюнкции относительно дизъюнкции: 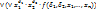 ,
,  (*)
(*) не содерж.переменных, т.е не явл высказыванием. Опуская в (*) все слагаемые, в которых истинность формулы f равна 0, получим, что
не содерж.переменных, т.е не явл высказыванием. Опуская в (*) все слагаемые, в которых истинность формулы f равна 0, получим, что  ,
,  ,
, 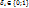 .
.

 )
)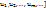 -исходный алфавит переменных(аргументов) и
-исходный алфавит переменных(аргументов) и 
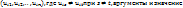 которой опред.на мн-ве
которой опред.на мн-ве 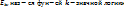 . Обозначим ч/з
. Обозначим ч/з  систему всех фун-ий k-значной логики над алфавитом U, содержащую также константы 0,1,..,k-1. Лемма. Число всех ф-ий из
систему всех фун-ий k-значной логики над алфавитом U, содержащую также константы 0,1,..,k-1. Лемма. Число всех ф-ий из  ОПР.Ф-я f(
ОПР.Ф-я f(  ) из
) из  переменных
переменных 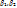 переменной
переменной  f(
f(  )
) 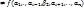
 = 21 = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица.
= 21 = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица. = 22 = 4. Определение этих функций содержится в следующей таблице.
= 22 = 4. Определение этих функций содержится в следующей таблице.

 = 24 = 16.
= 24 = 16.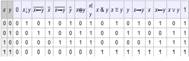
 = 28 = 256. Некоторые из них определены в следующей таблице:
= 28 = 256. Некоторые из них определены в следующей таблице: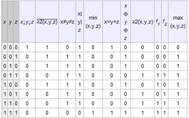
 (суперпозиция конъюнкции, дизъюнкции и двух отрицаний) будет соответствовать следующая таблица:
(суперпозиция конъюнкции, дизъюнкции и двух отрицаний) будет соответствовать следующая таблица:
 и множество всех унарных функций. А вот объединение замкнутых классов может таковым уже не являться. Например, объединив классы {0} и
и множество всех унарных функций. А вот объединение замкнутых классов может таковым уже не являться. Например, объединив классы {0} и  , мы с помощью суперпозиции
, мы с помощью суперпозиции  сможем получить константу 1, которая в исходных классах отсутствовала.
сможем получить константу 1, которая в исходных классах отсутствовала. . Если функция задана в виде ДНФ, то сначала убираем дизъюнкцию, используя при этом правило де Моргана, а все отрицания заменяем прибавлением единицы. После этого раскрываем скобки по обычным правилам, при этом учитываем, что четное число одинаковых слагаемых равно нулю (так как х+ х = 0), а нечетное число одинаковых слагаемых равно одному такому слагаемому.
. Если функция задана в виде ДНФ, то сначала убираем дизъюнкцию, используя при этом правило де Моргана, а все отрицания заменяем прибавлением единицы. После этого раскрываем скобки по обычным правилам, при этом учитываем, что четное число одинаковых слагаемых равно нулю (так как х+ х = 0), а нечетное число одинаковых слагаемых равно одному такому слагаемому. ( xy + 1)((x + 1)(y + 1) + 1)((y + 1)z + 1) + 1 = (xy + 1)(xy + x + y)(yz + z + 1) + 1 = (x + y)(yz + z + 1) + 1= xyz + yz + xz +yz + x + y + 1 = xyz + xz + x +y + 1.
( xy + 1)((x + 1)(y + 1) + 1)((y + 1)z + 1) + 1 = (xy + 1)(xy + x + y)(yz + z + 1) + 1 = (x + y)(yz + z + 1) + 1= xyz + yz + xz +yz + x + y + 1 = xyz + xz + x +y + 1.

