
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Рассуждение.Схемы правильных рассуждений. Суть прямых и косвенных методов доказательств.Рассуждение наз-ся правильным если из конъюнкции посылок Р1,Р2,…,Рn следует заключение Д. Р1,Р2,…,Рn т е кажд раз когда посылки истинны, Д заключение тоже истинно Схема правильного рассуждения: Прямое доказательство При прямом доказательстве задача состоит в том, чтобы подыскать такие убедительные аргументы, из которых по логическим правилам получается тезис. Например, нужно доказать, что сумма углов четырехугольника равна 360°.Отмечаем, что диагональ делит четырехугольник на два треугольника.Значит, сумма его углов равна сумме углов двух треугольников. Известно, что сумма угловтреугольника составляет 180°. Из таких положений выводим, что сумма углов четырехугольника равна 360°.В построении прямого доказательства можно выделить два связанных между собою этапа: отыскание тех, признанных обоснованными утверждений, которы способны быть убедительными аргументами для доказываемого положения установление логической связи между найденными аргументами и тезисом. Нередко первый этап считается подготовительным и под доказательством понимается дедукция, связывающая подобранные аргументы и доказываемый тезис. Косвенное доказательство Косвенное доказательство устанавливает справедливость тезиса тем, что вскрывает ошибочность противоположного ему допущения, антитезиса.В косвенном доказательстве рассуждение идет как бы окольным путем. Вместо того чтобы Прямо отыскивать аргументы для выведения из них доказываемого положения, формулируется антитезис, отрицание этого положения. Далее тем или иным способом показывается несостоятельность антитезиса. По закону исключенного третьего, если одно из противоречащих друг другу утверждений ошибочно, второе должно быть верным.Антитезис ошибочен, значит, тезис является верным.Поскольку косвенное доказательство использует отрицание доказываемогоположения, оно является, как говорят, доказательством от противного.Допустим, нужно построить косвенное доказательство таког тезиса: «Квадрат не является окружностью». Выдвигаетсяантитезис: «Квадрат есть окружность». Необходимо показать ложность этого утверждения. С этой целью выводим из него следствия. Если хотя бы одно из них окажется ложным, это будет означать, что и само утверждение, из которого выведено следствие, также ложно. Неверным является, в частности, такое следствие: у квадрата нет углов. Поскольку антитезис ложен, исходный тезис должен быть истинным  Предикаты и операции над ними. Предикаты это отображения произв-х множеств во мн-во высказыв-й. Пусть х1,х2,…,хn-символы произв природы. Эти перемен-е будем наз-тьпредметные.Пусть наборы этих перемен принадлмн-ву Ω, кот будназ-ть предметной обл-ю.Связное,повест, предлож-е,содерж-ее n-перемен-х и обладающеесвойством при фиксации переем-х,ожно сказать истинно оно или ложно,наз-ся значением истинности предиката.Пример: «х²<-1, х€R» Q(x)-одноместный предикат, Q(x)=0. Пусть Р(х1,х2,…,хn)- n-местный предикат,опр-й на Ω. Р-1({1})={( х1,х2,…,хn)€Ω|Р(х1,х2,…,хn)=1}-мн-во истинности предиката Р. Р-1({0})={( х1,х2,…,хn)€Ω|Р(х1,х2,…,хn)=0}-мн-во ложности предиката. Пусть Р(х1,х2,…,хn)- n-местный предикат,опр-й на Ω. Отрицанием предиката Р наз предикат Р(х1,х2,…,хn)= Р(х1,х2,…,хn),тоже самое на знач истинности Р(х1,х2,…,хn)= Р(х1,х2,…,хn) Дизъюнкцией (конъюнк,эквивалент,имплик-й) наз предикат опр-й на Ω обознач-й Д: P+Q; K:P^Q, P*QИ:P→Q, Э; Р~Q. 2 предиката наз-сяравными,если они равны друг другу при любом наборе переменных.. Множество n-местных предикатов опред-х на Ω обр-т булеву алгебру предикатов. Поэтому для них справедливы 19 оснравносильн-й булевой алгебры |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 373. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
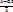 ,
,  .
.