
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод Жордана-Гаусса (обращения матриц). ⇐ ПредыдущаяСтр 8 из 8 Пусть имеется система линейных алгебраических уравнений: A.X = B Если эту систему уравнений умножить слева на обратную матрицу: A-1A . X = A-1 B то, учитывая, что A-1 А = Е (единичная матрица), получим: X = A-1 B (3.8) Таким образом, для того чтобы решить систему уравнений, необходимо одним из методов вычислить обратную матрицу и умножить ее на вектор правых частей системы. Этот метод удобен в тех случаях, когда система уравнений решается при различных правых частях. Тогда необходимо один раз вычислить обратную матрицу, а затем, меняя правые части, вычислять произведение этой матрицы на столбец. Итерационные методы. Запишем систему (3.5) в виде: x1 = (b1 - x2a12 - x3a13)/a11 x2 = (b2 - x1a21 - x3a23)/a22 (3.9) x3 = (b3 - x1a31 - x2a32 )/a33 или в матричном виде: X = b+ aX, где
X = x2 ; b = b2 x3 b3 a31 a32 0 Если для системы (3.9) будет выполнено хотя бы одно из условий: ║ ║ то итерационный процесс, задаваемый формулой: x(k+1) = b+ a x (k) (3.12) сходится к единственному решению, независимо от начального приближения. Таким образом, для того чтобы решить систему линейных уравнений (3.9), необходимо задаться некоторым начальным приближением х0, равным, например, вектору правых частей системы и вычислить значения х(1) по формуле (3.12). Если при этом │x(0) - x (1) │ ≤ ε (ε - точность вычислений), то значение х(1) можно принять за решение. В противном случае х(1) используется в правой части уравнения (3.12), и вычисляется значение х(2) и т.д.  Если систему уравнений (3.5) представить в виде: X = b+ a1X + a2X где
X = x2 ; b = b2 x3 b3 a31 a32 0 |
|||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 184. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 x1 b1 0 a12 a13
x1 b1 0 a12 a13 ; a = - a21 0 a23
; a = - a21 0 a23  ; (3.10)
; (3.10) ║1 = max
║1 = max  или ║
или ║  или
или  (
( 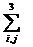 |α 2 ij |) ½ < 1 (3.11)
|α 2 ij |) ½ < 1 (3.11)