
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы численного интегрированияЗадача численного интегрирования функции заключается в вычислении значения определенного интеграла по ряду значений подынтегральной функции, т.е. в составлении интегральной суммы. Чем меньше интервалы разбиения (больше узловых точек, т.е. точек, в которых вычисляется значение подынтегральной функции), тем точнее будет вычислен интеграл. Для функции, заданной таблично, число узловых точек фиксировано, и задача вычисления интеграла обычно сводится к замене этой функции на рассматриваемом отрезке интерполирующей функцией простого вида, интеграл от которой вычисляется непосредственно. Для аналитически заданных функций возможны два способа выбора точек разбиения исходного интервала: либо число точек или интервалов фиксируется заранее, либо число и величины интервалов определяются в процессе вычисления интеграла в зависимости от заданной точности. В обоих случаях исходная функция на каждом интервале заменяется соответствующей зависимостью. 1. Метод прямоугольников основан непосредственно на определении интеграла
где
или
2. Метод трапеций основан на том, что график подынтегральной функции на каждом интервале разбиения заменяется стягивающей ее хордой, и площадь ограниченная функцией на интервале, заменяется площадью трапеции. В этом случае при равных интервалах формула метода трапеций имеет вид: 
Здесь: 3. Метод Симпсона основан на том, что через три ординаты двух соседних интервалов проводится парабола и получающиеся при этом площади складываются. В отличии от предыдущих методов здесь отрезок [a,b] следует делить на четное число интервалов (например, на 2n). Формула метода Симпсона при этом будет иметь вид:
4. Метод Чебышева состоит в том, что интеграл представляется в виде:
где Xi=(a+b)/2+ti(b-a)/2–абциссы ti приведены в табл.1, n - число узловых точек. При этом вывод ti определяется из условия, что формула 2.6 справедлива для всех полиномов f(Xi) до степени m включительно; m=2n-1 на интервале от –1 до +1. Подставляя в уравнение (2.6) функции: f(ti) = t1,t2, ..., tm-1,tm , и зная точное значение интеграла на интервале [-1¸+1] получим систему нелинейных алгебраических уравнений, в результате решения которой определяются значения ti. Для числа узловых точек n=2,3,4,5,6,7,9 значения ti приведены в таблице 1. Для n=8 и n>9 формула Чебышева неприменима.
Таблица № 1.
5. Метод Гаусса основан на том, что в формуле:
где Xi=a+(b-a)ti. Коэффициенты Ai и абциссы ti выводятся для интервала от –1 до +1 и приведены в табл. 2. На интервале от –1 до +1, выбор абсцисс t1, t2, ..., ti и коэффициентов А1,А2, ... Аi производится таким образом, чтобы формула 2.7 была точной для всех полиномов f(Xi) с наивысшей возможной степенью m. В этом случае коэффициенты Аi и положение узловых точек ti определяются решением системы уравнений, которая получается при подстановке f(ti)=1,t,t2,t3,...tm в левую и правую части формулы (2.7), где: n - число узловых точек, m=2n-1. Следует отметить, что абсциссы ti являются корнями полиномов Лежандра. Таблица № 2.
Так как точность методов численного интегрирования в значительной степени определяется величиной шага интегрирования. Для методов прямоугольников, трапеций, Симпсона изменение шага интегрирования не приводит к изменению формулы, точнее алгоритма вычислений. По этому интегрирование с переменным шагом заключается в том, что интеграл вычисляется многократно при различном числе точек разбиения исходного интервала, т.е., при различной величине шага, и каждый раз сравниваются две последующие интегральные суммы. Если разность между ними по модулю не превосходит заданной погрешности, то вычисления прекращаются, в противном случае производится дальнейшее изменение величины шага интегрирования, и расчеты повторяются. В простейшем случае изменение величины шага интегрирования производится путем последовательного увеличения числа узловых точек на определенное число (например, на единицу). Лабораторная работа № 3.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 160. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
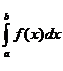
 (2.1)
(2.1) - интегральная сумма, соответствующая данному разбиению: x1, x2,..., xn - некоторые точки на интервалах разбиения, в которых вычисляются значения функции. Чаще всего отрезок [a,b] делится на равные части и в качестве узловых точек выбираются границы интервалов разбиения. В этом случае формулы метода прямоугольников имеет вид:
- интегральная сумма, соответствующая данному разбиению: x1, x2,..., xn - некоторые точки на интервалах разбиения, в которых вычисляются значения функции. Чаще всего отрезок [a,b] делится на равные части и в качестве узловых точек выбираются границы интервалов разбиения. В этом случае формулы метода прямоугольников имеет вид: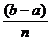 [f(x0)+ f(x1)+ ... + f(xn-1)] (2.2)
[f(x0)+ f(x1)+ ... + f(xn-1)] (2.2) [f(a)+4f(x1)+2f(x2)+...+4f(x2n-1)+2f(x2n-2)+...+f(b)] (2.5)
[f(a)+4f(x1)+2f(x2)+...+4f(x2n-1)+2f(x2n-2)+...+f(b)] (2.5)
 (2.7)
(2.7)