
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Принцип тождественности частиц. Симметричные и антисимметричные волновые функции. Бозоны и фермионы, принцип Паули.Будем называть одинаковыми частицы, имеющие одинаковые массы, заряды, спины и т.д. Такие частицы в равных условиях ведут себя одинаковым образом, теряют свою индивидуальность. Поэтому выполняется принцип тождественности частиц: состояния системы частиц, получающиеся друг из друга перестановкой тождественных частиц местами, нельзя различить ни в каком эксперименте и такие состояния следует рассматривать как одно и то же физическое состояние. Рассмотрим систему из N невзаимодействующих частиц, обладающих спином. Волновая функция такой системы имеет вид С другой стороны, по определению оператора: Подействуем на с учетом (2), получим: Как следует из (3) и (4), должно выполняться равенство: Опр. Функции, сохраняющие свое значение при перестановке аргументов, называются симметричными: В релятивистской квантовой механике доказывается, что частицы с целым спином должны иметь симметричные волновые функции, а частицы с полуцелым спином – антисимметричные. Электроны имеют полуцелый спин, поэтому описываются антисимметричными волновыми функциями. Частицы с целым спином называются бозонами, с полуцелым – фермионами. Примером бозона является фотон, примерами фермионов – электроны, протоны, нейтроны.  Рассмотрим систему из двух невзаимодействующих тождественных фермионов. Каждый из них описывается своей волновой функцией В силу тождественности фермионов эту функцию можно записать и в виде: Так как волновая функция двух фермионов должна быть антисимметричной и следует учесть два варианта представления (5) и (6), то запишем двухчастичную функцию в виде: где С – нормировочный множитель. Функцию (7) можно записать в виде определителя: По аналогии с (8) можно записать волновую функцию для N невзаимодействующих фермионов: Рассмотрим случай, когда два фермиона находятся в одинаковых состояниях. Это означает, что среди набора волновых функций две будут одинаковые, например Если рассмотреть систему из двух невзаимодействующих бозонов, то двухчастичная волновая функция бозонов запишется в виде: По аналогии с (10) волновая функция N невзаимодействующих бозонов будет иметь вид: где суммирование производится по всем перестановкам индексов i1i2…. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 479. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Введем обозначения:
. Введем обозначения:  , тогда в новых обозначениях волновая функция примет вид:
, тогда в новых обозначениях волновая функция примет вид:  . Введем оператор
. Введем оператор  перестановки двух частиц местами. Переставим, например, первую и вторую частицы:
перестановки двух частиц местами. Переставим, например, первую и вторую частицы: . (1)
. (1) . (2)
. (2) , (3)
, (3)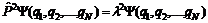 (4)
(4)
 . Функции, изменяющие знак при перестановке аргументов, называются антисимметричными:
. Функции, изменяющие знак при перестановке аргументов, называются антисимметричными:  .
. и
и  . Построим из этих функций волновую функцию двух фермионов
. Построим из этих функций волновую функцию двух фермионов  . Величина
. Величина  определяет вероятность совместного состояния двух фермионов, а величины
определяет вероятность совместного состояния двух фермионов, а величины  и
и  – вероятности для состояний для отдельных фермионов. Теорема об умножении вероятностей независимых событий будет выполняться, если двухчастичную волновую функцию записать в виде:
– вероятности для состояний для отдельных фермионов. Теорема об умножении вероятностей независимых событий будет выполняться, если двухчастичную волновую функцию записать в виде: . (5)
. (5) . (6)
. (6) , (7)
, (7) . (8)
. (8) . (9)
. (9) и
и 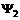 . Тогда в определителе (9) два столбца будут совпадать и определитель будет равен нулю. Т.е. такое состояние системы невозможно. Отсюда следует принцип Паули: два тождественных фермиона не могут находиться в одном квантовом состоянии.
. Тогда в определителе (9) два столбца будут совпадать и определитель будет равен нулю. Т.е. такое состояние системы невозможно. Отсюда следует принцип Паули: два тождественных фермиона не могут находиться в одном квантовом состоянии. . (10)
. (10)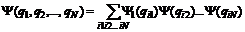 , (11)
, (11)