
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема про структуру лін. стаціонарної системи. ⇐ ПредыдущаяСтр 7 из 7
Теорема: Якщо rankSn= r<n , тобто справджується умова (2), то систему (1) за допомогою лінійного перетворення X(t)=T(y) (3) можна звести до системи Матриця У співвідношеннях (7) і (8) P1-матриця розміру - rxr; P2 – rx(n-r); P3 – (n-r)x(n-r) Q1 – rxm. Крім цього rank (Q1,P1,Q1,..,P1r-1Q1)=r (9) Доведення: Очевидно, що P=T-1AT; Q=T-1B. Покажемо, що лінійний підпростір породжений векторами K=(k1,k2,..,kr) збігається з гіперплощиною yr+1=0, yr+2=0,..,yn=0. (10). Запишемо перетворення
умову з гіперплощини (10), то ми там же і залишимося на
|
||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 238. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
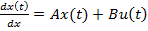 (1) Sn=(B,AB,A2B,..,An-1B) rankSn= r < n (2) k1,..,kr
(1) Sn=(B,AB,A2B,..,An-1B) rankSn= r < n (2) k1,..,kr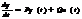 (4). При чому Т матриця має вигляд: Т=(k1,k2,..,kr,l1,..,ln-r) (5) де першими r стовпчиками є лінійно-незалежні стовпчики Sn, а решта n-rстовпців вибирають щоб виконувалася умова detT
(4). При чому Т матриця має вигляд: Т=(k1,k2,..,kr,l1,..,ln-r) (5) де першими r стовпчиками є лінійно-незалежні стовпчики Sn, а решта n-rстовпців вибирають щоб виконувалася умова detT 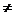 0 (6).
0 (6).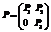 (7).
(7). 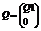 (8).
(8).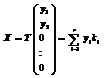
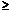 t0. Тоді структура матриць повинна бути, як описано в (7) і (8). Вектор y
подамо у вигляді
t0. Тоді структура матриць повинна бути, як описано в (7) і (8). Вектор y
подамо у вигляді
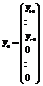 (11),
(11),