Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Подання розв’язку нестаціонарних лінійних систем керування через фундаментальний розв’язокЛінійна багатовимірна неперервна система керування описується рівнянням
Використаємо відомі результати з теорії лінійних диференціальних рівнянь зі змінними коефіцієнтами. З цієї теорії нам відомо, що лінійно-незалежні розв’язки
однорідного рівняння
утворюють фундаментальну матрицю
Фундаментальну матрицю можна знайти як розв’язок матричної задачі Коші
Для фундаментальної матриці існує обернена матриця
Знайдемо розв’язок рівняння (5.1) за нульових початкових умов. Запропонуємо наступний алгоритм. Диференціюючи рівність (5.5), одержимо
Використовуючи (5.4), останнє співвідношення перепишемо так:
Звідси
або
Співвідношення (5.6) помножимо на вектор
Замість виразу
або
Інтегруючи цю рівність в межах від 0 до
Помножимо останню рівність на матрицю
Зробивши позначення
рівність (5.7) запишемо у вигляді
(5.10) Поняття спряжених систем. Теорема про властивості розв’язків та фундаментальних матриць лінійних систем і спряжених систем  Означення 6.1 Дві системи, які описуються рівняннями
де Теорема 6.1 Нехай
Тоді справджуються рівності
Доведення. Розглянемо вираз
Тут використано означення транспонованої матриці. Отже рівність (6.4) доведена. Рівність (6.5) доведемо аналогічно. Дійсно, те що добуток
Оскільки при З рівності (6.5) випливає, що
Тому імпульсну перехідну матрицю (5.8) системи можна записати так:
З цієї причини спряжені системи грають важливу роль в теорії лінійних нестаціонарних систем.
Задача про керовність. Означення керовності. Розглянемо лін. нестац.сист.керуван. (1.1.) x(t) є Rn – n-вимірний векторu(t) є Rn – m – вимірний вектор A(t) –квадратна матрицяA(t)= B(t)= Вважаємо, що x(t) визнач.фазов. стан системи (1.1) і будемо говорити, що x(t) належ.фазовому простору Х, x(t) єХ. Ф( Ф(
Позначимо w(t, w(t, Розв.сист.(1.1), який задовол. початк. умову x(t0) = х0 можна записати у такому вигляді (1.5): x(t)=Ф(t, t0)x0+ Те, що x(t) є розв. (1.1), який задов. (1.6) легко перевырити. Для цього треба продиференц. ліву і праву част. (1.5) і підставити в (1.1) Нехай сист. керув. описується такою системою Чи можна підібрати так u(t), щоб траекторія проходила через х0,х1? Означ.:Система (1) називається цілком керовною , якщо для довільних
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 244. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
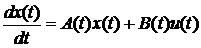 . (5.1)
. (5.1) (
( 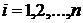 )
)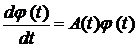 (5.2)
(5.2)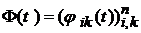 . (5.3)
. (5.3)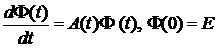 . (5.4)
. (5.4)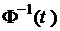 в такому розумінні, що
в такому розумінні, що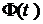 =
= 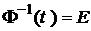 . (5.5)
. (5.5)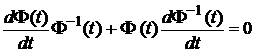 .
.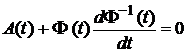 .
.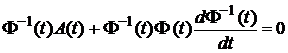
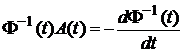 . (5.6)
. (5.6)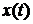 , який задовольняє рівняння (5.1) за початкових умов
, який задовольняє рівняння (5.1) за початкових умов 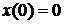 . Тоді одержимо
. Тоді одержимо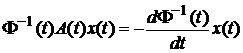 .
.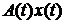 підставимо його значення з рівняння (5.1). Тоді
підставимо його значення з рівняння (5.1). Тоді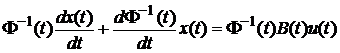
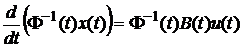 .
.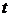 , одержимо
, одержимо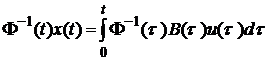 .
.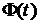 . Тоді остаточно маємо
. Тоді остаточно маємо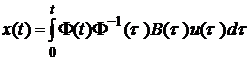 . (5.7)
. (5.7)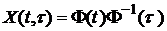 (5.8)
(5.8)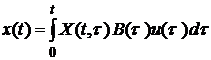 . (5.9)
. (5.9)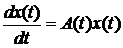 (6.1)
(6.1)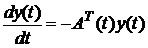 , (6.2)
, (6.2)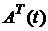 – матриця транспонована до матриці
– матриця транспонована до матриці 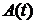 , називаються спряженими.
, називаються спряженими.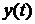 – деякі розв’язки рівнянь (6.1) і (6.2);
– деякі розв’язки рівнянь (6.1) і (6.2); 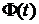 і
і 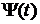 – фундаментальні матриці цих рівнянь, тобто
– фундаментальні матриці цих рівнянь, тобто 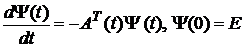 . (6.3)
. (6.3)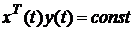 ; (6.4)
; (6.4)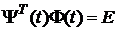 . (6.5)
. (6.5)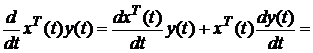
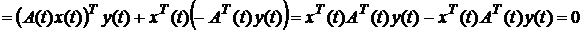
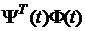 сталий випливає з того, що
сталий випливає з того, що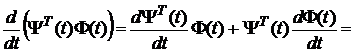
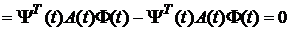 .
.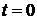 цей добуток дорівнює
цей добуток дорівнює 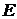 (обидві матриці при
(обидві матриці при 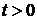 за теоремою існування і єдиності розв’язку однорідної системи диференціальних рівнянь.
за теоремою існування і єдиності розв’язку однорідної системи диференціальних рівнянь.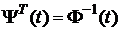 .
.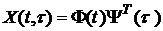 .
.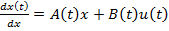
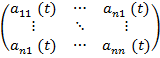
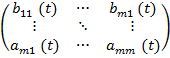
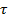 ) - норм.фундамент.матр.розв.лін. одн. системи, яка відновл.сист.(1.1)
) - норм.фундамент.матр.розв.лін. одн. системи, яка відновл.сист.(1.1)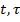 ) – розв.наступ.матр.задачі Коші
) – розв.наступ.матр.задачі Коші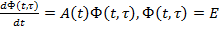 (1.3)
(1.3)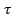 ) матрицею імпульсних перехідних фнкцій для сист.(1.1)
) матрицею імпульсних перехідних фнкцій для сист.(1.1)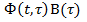 (1.4)
(1.4)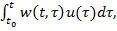 причому x(t0) = х0 (1.6)
причому x(t0) = х0 (1.6)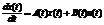 (1) t0<=t1-моменти часу ; x - n-вимірний вектор; u – m-вимірний вектор ; A(t) – nxn, В(t) – nxm. A,B-неперервні, інтегровні (припускаєм)
(1) t0<=t1-моменти часу ; x - n-вимірний вектор; u – m-вимірний вектор ; A(t) – nxn, В(t) – nxm. A,B-неперервні, інтегровні (припускаєм)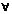 t0 , t1 : t0<t1 ;
t0 , t1 : t0<t1 ; 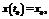
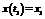 (2).
(2).