
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема про необхідні і достатні умови керовності.Нех. СК описується такою с-мою ДР. (1): Доведення. 1)Достатність: Запишемо розв’язок с-ми (1),який задовольняє поч. умову x(t0)=x0 : він має такий вигляд:
2)Необх. Тобто,треба показати таку річ: Нехай с-ма (1) цілком керовна,але вектор-рядочки матриці (1.6) лін. залежні. Поки що таке неможливе. Нехай існує вектор l,l<>0 lTW(t1,τ )=0 τ є [t0,t1], =>,що існує таке керування U(t),що розв’язок (1.1) задовольняє умови (1.2) ¥ x0,x1.(при цьому керуванні). Виберемо вектори x0 і x1 так,щоб вик. умова:lT(x1-X(t,t0)x0)<>0 (2.10). Тоді,якою б не була ф-ія U(t) (=>із(2.9))  стану x0 в x1: (це просто міркування) А тепер інтегруємо
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 234. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Запишемо таку крайову умову(2) для с-ми (1): x(t0)=x0 є X, x(t1)=x1 є X, t є [t0, t1] Теорема1(Критерій цілком керовності с-ми(1)-(2)): Для того, щоб система (1),(2) була цілком керовною, н. і д., щоб вектор функцій
Запишемо таку крайову умову(2) для с-ми (1): x(t0)=x0 є X, x(t1)=x1 є X, t є [t0, t1] Теорема1(Критерій цілком керовності с-ми(1)-(2)): Для того, щоб система (1),(2) була цілком керовною, н. і д., щоб вектор функцій 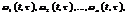 при
при 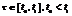 були лін.незал.
були лін.незал.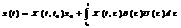 . Для того, щоб с-ма (1) була цілком керовною треба підібрати ф-ію U(t) так, щоб виконувалася рівність:
. Для того, щоб с-ма (1) була цілком керовною треба підібрати ф-ію U(t) так, щоб виконувалася рівність:  (2.2), або треба, щоб виконувалася така рівність
(2.2), або треба, щоб виконувалася така рівність 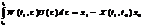 (2.3).Якщо знайдеться хоча б 1 така ф-ія, то їх можна підібрати дуже багато. Покажемо, що якщо вектор ф-ія (1) лін. незал., то можна таку ф-ію побудувати. Шукатимемо ф-ію U0(t) у такому вигляді: U0(t)=WT(t,τ )l (2.4),де l- невідомий сталий вектор. Підставимо (2.4) в (2.3):
(2.3).Якщо знайдеться хоча б 1 така ф-ія, то їх можна підібрати дуже багато. Покажемо, що якщо вектор ф-ія (1) лін. незал., то можна таку ф-ію побудувати. Шукатимемо ф-ію U0(t) у такому вигляді: U0(t)=WT(t,τ )l (2.4),де l- невідомий сталий вектор. Підставимо (2.4) в (2.3):  Wl=C;
Wl=C;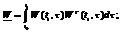 Якщо виявиться, що матриця Wє неособливою, тобто для неї вик. умова (2.5) detW<>0,то із р-ня ми знайшли б l однозначно: l=W-1*C(2.6). Покажемо, що за умов т-ми виконується умова (2.5).Виберемо б/я вектор q є Rn,такий, що ||q||>0 (тобто, що хоча б 1 компонента <>0) [ ||q||2=qT*q=Σqi2, i=1,n ]. Тоді, за умовою т-ми, для цілого q : ||qTW(t1,τ )||2>0, τ є [t0,t1] , тоді можемо записати: (2.7)
Якщо виявиться, що матриця Wє неособливою, тобто для неї вик. умова (2.5) detW<>0,то із р-ня ми знайшли б l однозначно: l=W-1*C(2.6). Покажемо, що за умов т-ми виконується умова (2.5).Виберемо б/я вектор q є Rn,такий, що ||q||>0 (тобто, що хоча б 1 компонента <>0) [ ||q||2=qT*q=Σqi2, i=1,n ]. Тоді, за умовою т-ми, для цілого q : ||qTW(t1,τ )||2>0, τ є [t0,t1] , тоді можемо записати: (2.7)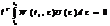 ,а оск. с-ма цілком керовна,то її розв’язок можна записати у вигляді (2.2) або (2.3), тоді маємо:
,а оск. с-ма цілком керовна,то її розв’язок можна записати у вигляді (2.2) або (2.3), тоді маємо: 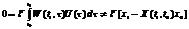 (2.11).Що суперечить умові цілком керовності. ТД. Наслідок: Покажемо,що ф-ія U0(t),побудована у процесі доведення т-ми,має таку вл-ть (для цілком керовної с-ми): ¥ іншої ф-ії U(t)<>U0(t),яка переводить с-му (1.1) із стану x0 в стан x1,справджується нерівність:
(2.11).Що суперечить умові цілком керовності. ТД. Наслідок: Покажемо,що ф-ія U0(t),побудована у процесі доведення т-ми,має таку вл-ть (для цілком керовної с-ми): ¥ іншої ф-ії U(t)<>U0(t),яка переводить с-му (1.1) із стану x0 в стан x1,справджується нерівність:  (2.12).Щоб це показати розглянемо таку р-ть: ||U(t)||2-2U0T(t)(U(t)-U0(t))=||U(t)||2+||U(t)-U0(t)||2 , [ де ||U(t)||2=UT(t)*U(t) ,тобто, ||U(t)||2=UT(t)*U(t)=ΣUi2(t), i=1,m ]. Проінтегруємо р-ть (2.13) в межах від t0 до t1 і врахуємо,що U(t) – керування,при якому розв’язок переходить із
(2.12).Щоб це показати розглянемо таку р-ть: ||U(t)||2-2U0T(t)(U(t)-U0(t))=||U(t)||2+||U(t)-U0(t)||2 , [ де ||U(t)||2=UT(t)*U(t) ,тобто, ||U(t)||2=UT(t)*U(t)=ΣUi2(t), i=1,m ]. Проінтегруємо р-ть (2.13) в межах від t0 до t1 і врахуємо,що U(t) – керування,при якому розв’язок переходить із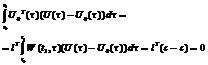
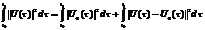 (звідси→(2.12))
(звідси→(2.12))