
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лема про ранг матриці керовності лін. стаціон. с-миЯкщо ранг матр. Sn: rank Sn = r≤n, то 1) rank Sr = r (1) 2)б/я стовпчик матр. Sn можна виразити ч/з r лін.незал. стовпців матр. Sr ; або як лін. комбінацію лін.незал. стовпців матр. Sr. Дов-ня. Розгл. bj, Ab,…, An-1bj (2). Нех. серед цих векторів rj лін.незал.векторів. Покаж., що цими век-ми є век-ри: bj, Ab,…, Ar-1bj ( (rj-перших век-рів). Дов-ня від супрот. Нех. це не так, тобто у (2) mj век-рів: mj<rj-лін.незал., а mj+1 лін. вираж-ся ч/з mj-век-рів. І решта rj-mj знах. між mj+1 . bj, Ab,…, Amj-1bj, Amjbj, Amj+1bj,… An-1bj, це mj лін.незал., тому => Amjbj = (3) Серед коеф-в -є хоча б 1 відмін. від 0. Домнож. (3)*А зліва Amj+1 bj = = = = (4) Домнож. (4)*А (зліва), одерж.: Amj+2 bj = ………….. An-1 bj = .Вказані рівності показ., що кожен век-р почин-чи з n+1 є лін. комбін-ю mj перших векторів => mj=rj. Далі міркуємо так: беремо з сукупності Sn = (B, AB,…An-1B) (n*m-стовпців) почерзі вектори: b1, Ab1,…, An-1b1, де шукаємо ранг, як макс-ну кіль-ть лін.незал. век-рів r1<r; Далі b2, Ab2,…, An-1b2,, де r1+r2=r , r2<r. І так далі, поки rn=r . Щоб довести 2) ми зробимо так: Якщо вектор належ. сукуп-ті лінійнонезал-х векторів, то він вираж-ся сам ч/з себе. Б/я інший вектор належ-ть одній із груп типу (2). Тоді цей вектор можна подати як ліню комб-ю лін.незал. век-рів викор-чи попер. міркування, а це означ. правильність твердження.
13. Критерій керованості лін. стац. системи.
Теорема(про необх. і дост. умови цілком керованості лінійної стаціонарної системи ): Для того, щоб система (1) була цілком керованою, н. і д., щоб Доведення. Достатність. Нехай (3) виконується. Покажемо, що вектор-рядки матриці імпульсної перехідної функції є лінійно незалежними 
Останню нерівність продиференціюємо по
X(t,
lTX(t,
З (10) rankSn<n =>
Лема про інваріантний підпростір лінійної стаціонарної системи . Розглянемо стаціонарну систему
і припустимо, що для неї не викон.умова цілком керованості і rankSn= r<n (6.2) K1, K2 ,...,Kr – лін.незал. стовпчики матр. Sn, тоді виконується лема : Лема:Якщо для сист. (6.1) викон. умова (6.2) то підпростір Kr= {k1,…,kr} (6.3) є інваріантним підпростором для сист. (6.1). Тобто це означає, що якщо x0є Kr, то р – ок (6.1) який задов. початк. ум. X(t0) = x0 (6.4) також належить x(t)Kr Дов-ня: Запишемо р-ок (6.1), який задов. умову (6.4). Цей р-ок має вигляд: x(t) = eA(t-t0)x0 +
Використаємо подання eAt як:
(6.5) Врахуємо, щоx0 =
Розглянемо
x(t) =
Якщо позначити [] через λР(t), то: x(t) =
Sn = (B, AB,…An-1B)rank Sn = r < n (7.2)
|
||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 256. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1) Sn=(B,AB,A2B,..,An-1B) (2)
(1) Sn=(B,AB,A2B,..,An-1B) (2) .
. .. Доведення проведемо від супротивного. Нехай вектор-рядки матриці (4) будуть лінійно залежними, тобто існує n-вимірнійсталий вектор l.
.. Доведення проведемо від супротивного. Нехай вектор-рядки матриці (4) будуть лінійно залежними, тобто існує n-вимірнійсталий вектор l. ,
,  (5)
(5) n-1 раз і розглянемо наступні співвідношення
n-1 раз і розглянемо наступні співвідношення  ,
, .(6)
.(6)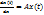 (7)
(7)

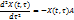




 вектор-рядки матриці (2) – лінійно-залежні
вектор-рядки матриці (2) – лінійно-залежні  , а це суперечить умові (3). Необхідність: Нехай вектор-рядки матриці (4), лінійно незалежні, тобто система цілком керована. Покажемо, що справджується умова (3). Нехай це не так, тобто
, а це суперечить умові (3). Необхідність: Нехай вектор-рядки матриці (4), лінійно незалежні, тобто система цілком керована. Покажемо, що справджується умова (3). Нехай це не так, тобто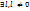

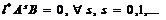 на основі Леми1.
на основі Леми1. 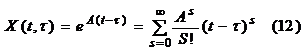
 ,
,  , Отже ми одержимо, що система не цілком керована, а це суперечить умові теореми.
, Отже ми одержимо, що система не цілком керована, а це суперечить умові теореми.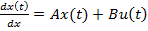 (6.1)
(6.1) t, t ≥ t0
t, t ≥ t0

 (6.6)
(6.6) . На основі леми про ранг керованості матриці ми можемо стверджувати, що цей вектор можна подати, як Kr {k1…kr}.
. На основі леми про ранг керованості матриці ми можемо стверджувати, що цей вектор можна подати, як Kr {k1…kr}. =
=  (6.7)
(6.7) =
=  (6.8)
(6.8) За лемою (1) кожний стовпчик
За лемою (1) кожний стовпчик ми можемо подати, як мін. комб. вектора (k1, k2, …, kr)
ми можемо подати, як мін. комб. вектора (k1, k2, …, kr) kp (6.9)
kp (6.9) =
=  =
=  =
= (6.10)
(6.10) (7.1)
(7.1)