
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Перехідна та імпульсна перехідна функції лінійних систем керування.Нехай математична модель керування задана рівнянням n – ого порядку
Розглянемо таку одиничну функцію:
Озн.: Реакція системи (1) на вхідний сигнал (2) називається перехідною функцією системи, якщо до моменту подачі вхідного сигналу система знаходилась у стані спокою. Позначається Перехідна функція – це розв’язок такої задачі: (3)-(4): Озн.: імпульсною перехідною функцією
Властивості ф-ї. Дірака:
δможна подати у вигляді 2х вхідних сигналів, що мають протилежніінтенсивності,тоді
Зв’язок між вхідним і вихідним сигналами лінійної одновимірної системи керування Розглянемо одновимірну лінійну систему зі змінними параметрами, яка описується рівнянням
Нехай система до моменту подачі вхідного сигналу знаходиться в стані спокою. За початок відліку часу виберемо момент подачі вхідного сигналу і початкові умови запишемо у вигляді
Знайдемо інтегральний зв’язок між вхідним Нехай 
З теорії диференціальних рівнянь відомо, що розв’язок неоднорідного рівняння (2.1) за умови (2.2) можна подати у вигляді
де
а
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 228. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
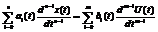 (1) .
(1) .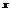 – одновимірний сигнал (функція), яка має багато похідних.
– одновимірний сигнал (функція), яка має багато похідних. 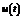 – подається на вхід системи.
– подається на вхід системи. 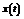 – реакція системи на
– реакція системи на 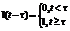 (2).
(2). 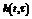 .
.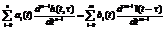 (3).
(3). 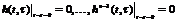 (4).
(4). 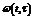 системи (1) називається реакція системи на вхідний сигнал типу одиничного імпульсу, якщо до моменту подачі вхідного сигналу система знаходилась в стані спокою.
системи (1) називається реакція системи на вхідний сигнал типу одиничного імпульсу, якщо до моменту подачі вхідного сигналу система знаходилась в стані спокою. 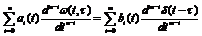 (5)
(5) 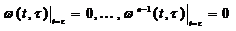 (6)
(6)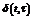 –ф-ія Дірака
–ф-ія Дірака 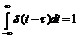 ,
, 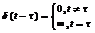 (7)
(7)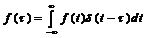 (8)
(8) 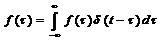 (9)
(9) 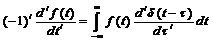 (10).
(10).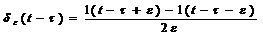
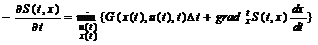 – рівняння Беллмана в диференціальній формі.
– рівняння Беллмана в диференціальній формі. 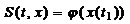 – крайова умова (записується із вигляду ф-ції S(t,x):
– крайова умова (записується із вигляду ф-ції S(t,x): 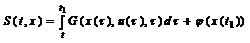 .
.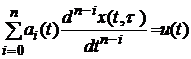 . (2.1)
. (2.1)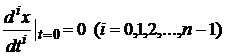 . (2.2)
. (2.2)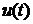 і вихідним
і вихідним 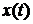 сигналами системи (2.1) за умови (2.2).
сигналами системи (2.1) за умови (2.2).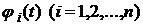 лінійно-незалежні розв’язки однорідного рівняння
лінійно-незалежні розв’язки однорідного рівняння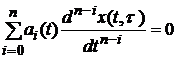 . (2.3)
. (2.3)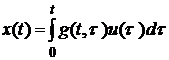 , (2.4)
, (2.4)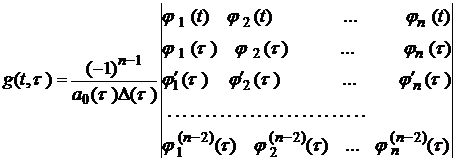 , (2.5)
, (2.5)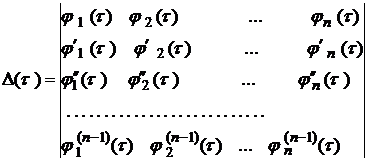 .
.