
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Які оцінки називаються незміщеними, зміщеними? Наведіть приклади.СМЕЩЕННАЯ ОЦЕНКА - статистическая оценка, математич. ожидание к-рой не совпадает с оцениваемой величиной.
не равна тождественно нулю, т. е. если
В таком случае статистика
является С. о. дисперсии
т. е. оценка S2n имеет смещение
Наилучшей несмещенной оценкой параметра
3. Які оцінки називаються незміщеними, зміщеними? Наведіть приклади. Чи є вибіркова дисперсія Для того чтобы охарактеризовать рассеяние значений количественного признака Xгенеральной совокупности вокруг своего среднего значения, вводят сводную характеристику - генеральную дисперсию. Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения  Если все значения x1, х2, …, xNпризнака генеральной совокупности объема N различны, то
Если же значения признака x1, х2, …, xkимеют соответственно частоты N1, N2,…, Nk,причем N1+N2+…+Nk=N, то
т.е. генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам. 4. Запишіть формулу для обчислення незміщеної оцінки Пусть из генеральной совокупности в результате nнезависимых наблюдений над количественным признаком Xизвлечена повторная выборка объема n:
При этом n1+ n2 + ... + nk= п. Требуется по данным выборки оценить (приближенно найти) неизвестную генеральную дисперсию Dг. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная дисперсия является смещенной оценкой Dг, другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить Dвна дробь n/(n-1). Сделав это, получим исправленную дисперсию, которую обычно обозначают через s2:
Исправленная дисперсия является, конечно, несмещенной оценкой генеральной дисперсии. Действительно,
Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию
Для оценки же среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:
Подчеркнем, чтоsне является несмещенной оценкой; чтобы отразить этот факт, мы написали и будем писать далее так: «исправленное» среднее квадратическое отклонение. |
||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 226. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 и пусть Т=Т (Х) -точечная статистич. оценка функции
и пусть Т=Т (Х) -точечная статистич. оценка функции  заданной на параметрич. множестве
заданной на параметрич. множестве 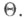 Предполагается, что математич. ожидание
Предполагается, что математич. ожидание  оценки Тсуществует. Если в этих условиях функция
оценки Тсуществует. Если в этих условиях функция
 то Тназ. смещенной оценкой функции
то Тназ. смещенной оценкой функции  а сама функция
а сама функция  наз. смещением или систематической ошибкой оценки Т.
наз. смещением или систематической ошибкой оценки Т.  распределенные случайные величины и пусть
распределенные случайные величины и пусть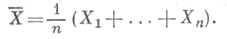

 так как
так как
 при этом квадратичный риск этой С. о. равен
при этом квадратичный риск этой С. о. равен
 является статистика
является статистика квадратичный риск к-рой равен
квадратичный риск к-рой равен 
 т. е. для | а| можно построить только С.
т. е. для | а| можно построить только С. незміщеною оцінкою генеральної дисперсії
незміщеною оцінкою генеральної дисперсії  ? Який дріб називають поправкою Бесселя?
? Який дріб називають поправкою Бесселя? .
.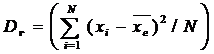 .
. ,
, генеральної дисперсії
генеральної дисперсії  .
. .
.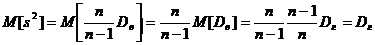 .
. .
. .
.