
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства дисперсии случайной величины1. Дисперсия постоянной величины С равна нулю
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин
4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение. Средним квадратическим отклонением
Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность значений случайной величины.
2) Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох определяется равенством
если интеграл сходится, или равносильным равенством
В частности, если все возможные значения Х принадлежат интервалу
или
Все свойства математического ожидания и дисперсии для дискретных случайных величин справедливы и для непрерывных величин. Среднее квадратическое отклонение непрерывной случайной величины определяется равенством
Моменты случайных величин. Среди числовых характеристик СВ особое значение имеют моменты–начальные и центральные. Начальным моментом k-го порядка СВ X называется математическое ожидание k-ой степени этой величины:
Центральным моментом k-го порядка СВ X называется математическое ожидание k-ой степени отклонения СВ X от ее математического ожидания. 
При k=1 первый начальный момент СВ X есть ее математическое ожидание, т.е. Центральные моменты
Например,
Биномиальное распределение и его характеристики. Если CВ Х принимает значения, равные 0, 1, 2…n с соответствующими вероятностями, представленными в таблице:
то имеем дело с биномиальным законом распределения. Очевидно, что определение биномиального закона распределения корректно, так как основное свойство ряда распределения выполнено, ибо
Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, вычисляются соответственно по формулам: M(X)=np D(X)=npq Распределение Пуассона. Рассмотрим дискретную случайную величину Х, принимающую только целые неотрицательные значения (0, 1, 2,…, т,…), последовательность которых бесконечна, но счетна. Такая случайная величина называется распределенной по закону Пуассона, если вероятность того, что она примет значение т, выражается формулой Пуассона: P(X=m)= где λ – некоторая положительная величина, называемая параметром закона Пуассона. Ряд распределения Пуассона имеет вид:
Очевидно, что определение закона Пуассона корректно, так как основное свойство ряда распределения выполнено, ибо сумма всех вероятностей равна 1:
Математическое ожидание и дисперсия случайной величины Х,распределенной по закону Пуассона, вычисляются соответственно по формулам: M ( X ) = λ D( X ) = λ
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 163. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. .
. .
. .
. случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии
случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии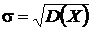 .
.
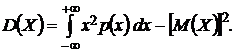
 , то
, то 

 .
.

 ;при k=2 второй центральный момент–дисперсия, т.е.
;при k=2 второй центральный момент–дисперсия, т.е. 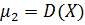
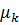 могут быть выражены через начальные моменты
могут быть выражены через начальные моменты 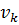 по формулам:
по формулам: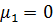


 и т.д.
и т.д.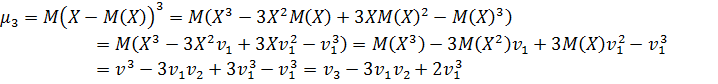
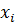



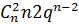

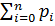 есть не что иное, как сумма всех членов разложения бинома Ньютона (отсюда и название закона – биномиальный):
есть не что иное, как сумма всех членов разложения бинома Ньютона (отсюда и название закона – биномиальный):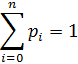
 ,
, 


