
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства условных вероятностей1)
Определение 3. Событие А называется независимым от события В
Теорема умножения вероятностей. Вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило
В частности для независимых событий Следствие.Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, вычисленную в предположении, что все предыдущие события уже наступили
В частности, вероятность совместного наступления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий
Вычисление вероятности появления хотя бы одного из совместных событий
В частности, если все n событий имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
7. Формула полной вероятности. Формула Байеса Определение. Набор событий Формула полной вероятности. Пусть события  Формула Байеса. Если событие А произошло, то условные вероятности (апостериорные) гипотез
где Р(А) — вероятность события А, вычисленная по формуле полной вероятности.
8. Формула Бернулли Ряд классических распределений связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания. Последовательные испытания называются независимыми, если вероятность осуществления любого исхода в n-м по счету испытании не зависит от реализации исходов предыдущих испытаний. Простейшим классом повторных независимых испытаний является последовательность независимых испытаний с двумя исходами («успех» и «неуспех») ис неизменными вероятностями «успеха» (р) и «неуспеха» Вероятность получить ровно m успехов в n независимых испытаниях вычисляется по формуле, называемой формулой Бернулли
Определение. Число наступлений события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз. Наивероятнейшее число наступлений события А в n испытаниях заключено между числами
9. Формула Пуассона Теорема 1 (Пуассона). Предположим, что произведение В случае, когда n велико, а р мало (обычно
10. Локальная и интегральная теоремы Лапласа Теорема 2 (Локальная теорема). Если вероятность наступления события А в каждом из n независимых испытаниях равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Теорема 3 (Интегральная теорема). Если вероятность наступления события А в каждом из n независимых испытаний равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n испытаниях число успехов m находится между
Из интегральной теоремы Лапласа можно получить формулу
11. Дискретные случайные величины Случайной называют величину, которая в результате испытания примет одно и только одно из возможных значений, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Обозначают случайные величины буквами Х, Y, Z, а их возможные значения — х, у, z. Дискретной называют случайную величину, которая принимает отдельные, изолированные друг от друга значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным. Дискретная случайная величина может быть задана рядом распределения — это соответствие между возможными значениями и их вероятностями:
События Ряд распределения дискретной случайной величины можно изобразить графически в виде полигона или многоугольника распределения вероятностей. Для этого по горизонтальной оси в выбранном масштабе нужно отложить значения случайной величины, а по вертикальной — вероятности этих значений, тогда точки с координатами Дискретная случайная величина может быть задана функцией распределения.Функцией распределения случайной величины Х называется функция Функцию
Если значения случайной величины — точки на числовой оси, то геометрически функция распределения интерпретируется как вероятность того, что случайная величина Х попадает левее заданной точки х:
12. Непрерывные случайные величины Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек. Примеры непрерывных случайных величин: диаметр детали, которую токарь обтачивает до заданного размера, рост человека, дальность полета снаряда и др. Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю Следствие. Если Х — непрерывная случайная величина, то вероятность попадания случайной величины в интервал
Если непрерывная случайная величина Х может принимать только значения в границах от а до b (где а и b — некоторые постоянные), то функция распределения ее равна нулю для всех значений Для непрерывной случайной величины Все свойства функций распределения дискретных случайных величин выполняются и для функций распределения непрерывных случайных величин. Задание непрерывной случайной величины с помощью функции распределения не является единственным.
13. Функция распределения вероятностей
1) Функция распределения дискретной случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x: F(X)=P(ξ<X). F(x) обладает свойствами: 1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: Утверждение следует из того, что функция распределения — это вероятность. 2. Функция распределения есть неубывающая функция на всей числовой оси. 3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна 1, т.е. 4. Вероятность попадания случайной величины в интервал
2) Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю Следствие. Если Х — непрерывная случайная величина, то вероятность попадания случайной величины в интервал
Если непрерывная случайная величина Х может принимать только значения в границах от а до b (где а и b — некоторые постоянные), то функция распределения ее равна нулю для всех значений Для непрерывной случайной величины: Все свойства функций распределения дискретных случайных величин выполняются и для функций распределения непрерывных случайных величин. Задание непрерывной случайной величины с помощью функции распределения не является единственным.
14. Плотность распределения вероятностей Плотностью вероятности (плотностью распределения или плотностью) р(х) непрерывной случайной величины Х называется производная ее функции распределения Плотность вероятности р(х), как и функция распределения F(х), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин. Плотность вероятности иногда называют дифференциальной функцией, или дифференциальным законом распределения. График плотности вероятности называется кривой распределения. Свойства плотности вероятности непрерывной случайной величины: 1. 2.
3.
4. Геометрически свойства плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
15. Математическое ожидание случайной величины и его свойства |
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 197. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ; 2)
; 2)  ; 3)
; 3)  ; 4) если
; 4) если  , то
, то  ;
; .
. , если
, если  , т.е. вероятность наступления события А не зависит от того, произошло событие В или нет.
, т.е. вероятность наступления события А не зависит от того, произошло событие В или нет. .
. , т.е. вероятность совместного наступления двух независимых событий равна произведению вероятностей этих событий.
, т.е. вероятность совместного наступления двух независимых событий равна произведению вероятностей этих событий. .
.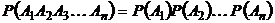 .
. можно вычислять как разность между единицей и вероятностью произведения противоположных событий
можно вычислять как разность между единицей и вероятностью произведения противоположных событий  :
: .
. .
. называется полной группой событий, если они попарно несовместны и их сумма составляет достоверное событие
называется полной группой событий, если они попарно несовместны и их сумма составляет достоверное событие
 образуют полную группу событий (
образуют полную группу событий (  ) и событие А может произойти с одним и только с одним из этих событий. Тогда вероятность события А равна
) и событие А может произойти с одним и только с одним из этих событий. Тогда вероятность события А равна  .
. вычисляются по формуле Байеса
вычисляются по формуле Байеса ,
, в каждом испытании (схема испытаний Бернулли).
в каждом испытании (схема испытаний Бернулли).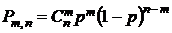 .
. и
и  :
:  . Если
. Если  .
. является постоянной величиной, когда n неограниченно возрастает. Обозначим
является постоянной величиной, когда n неограниченно возрастает. Обозначим  Тогда для любого фиксированного
Тогда для любого фиксированного  и любого постоянного
и любого постоянного 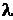 :
: 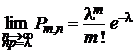 .
.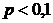 ;
; 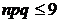 ) вместо формулы Бернулли применяют приближенную формулу Пуассона
) вместо формулы Бернулли применяют приближенную формулу Пуассона , где
, где  того, что в n испытаниях событие А наступит
того, что в n испытаниях событие А наступит  , где
, где  ,
,  .
. и
и  , приближенно равна (чем больше n, тем точнее)
, приближенно равна (чем больше n, тем точнее) , где р — вероятность появления успеха в каждом испытании,
, где р — вероятность появления успеха в каждом испытании, 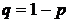 ,
,  .
. .
.




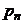
 ,
,  .
.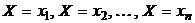 образуют полную группу, следовательно, сумма вероятностей этих событий равна единице:
образуют полную группу, следовательно, сумма вероятностей этих событий равна единице:  .
. будут изображать полигон распределения вероятностей; соединив же эти точки отрезками прямой, получим многоугольник распределения вероятностей.
будут изображать полигон распределения вероятностей; соединив же эти точки отрезками прямой, получим многоугольник распределения вероятностей. , выражающая для каждого х вероятность того, что случайная величина Х примет значение меньшее х:
, выражающая для каждого х вероятность того, что случайная величина Х примет значение меньшее х: 

 .
. не зависит от того, является этот интервал открытым или закрытым, т.е.
не зависит от того, является этот интервал открытым или закрытым, т.е. .
. и единице для значений
и единице для значений  .
. .
. .
. ;
; 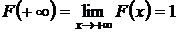 .
.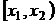 (включая
(включая  .
. .
. .
. (рис. 8.1).
(рис. 8.1).
 (рис. 8.2).
(рис. 8.2).
 .
.