
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Гидростатическое давление и его свойства. Физический смысл. Размерность в системных и внесистемных единицахВ гидростатике рассматривают жидкость, находящуюся в относительном покое. Основным понятием гидростатики является понятие гидростатического давления. Рассмотрим произвольный объем покоящейся жидкости (рис. 1.4).
Рис. 1.4. К понятию гидростатического давления
Если этот объем рассечь произвольно выбранной плоскостью и мысленно отбросить одну часть, то для сохранения равновесия оставшейся части необходимо к площадке w приложить каким-то образом распределенные силы, эквивалентные действию отброшенной части на оставшуюся. Пусть сила P представляет собой равнодействующую всех сил, приложенных к различным точкам площадки w, определяющих воздействие отброшенной части объема жидкости на площадку wоставшейся части этого объема. Тогда отношение (1.13) представит собой гидростатическое давление p на площадку:
Гидростатическим давлением в данной точке называется предел отношения силы давления покоящейся жидкости P к площади ее действия w при величине площадки, стремящейся к нулю, т.е.
или Гидростатическое давление в данной точке - величина конечного измерения. Гидростатическое давление обладает двумя основными свойствами. Первое свойство.Гидростатическое давление действует нормально к площадке и является сжимающим, т.е. оно направлено внутрь того объема жидкости, давление на который рассматриваем. Может ли гидростатическое давление быть направлено не по нормали? Если гидростатическое давление направлено не по нормали, то его можно разложить на нормальную и касательную составляющие. В соответствии с законом трения Ньютона касательные напряжения возникают при наличии градиента скорости, а мы рассматриваем покоящуюся жидкость (или другими словами, касательные напряжения должны привести к движению слоев жидкости, а мы рассматриваем покой).  Таким образом, давление в покоящейся жидкости может быть направлено только по нормали. Особыми физическими опытами доказано, что покоящаяся жидкость в определенных условиях иногда способна сопротивляться равномерному всестороннему растяжению. В обычных условиях растяжение жидкости будет отличаться от равномерного всестороннего, поэтому в ней будут возникать касательные напряжения и жидкость будет течь под действием растягивающих усилий. Кроме того, в обычных условиях даже при небольших растягивающих усилиях при всестороннем растяжении возникает разрыв (образование прогазовой прослойки) в жидкости. Имея это в виду, считают, что в обычной практической обстановке жидкость не сопротивляется касательным и растягивающим усилиям. Учитывая это, очевидно, следует сделать вывод, что давление в покоящейся жидкости всегда направлено по нормали к площадке действия внутрь рассматриваемого объема жидкости. Второе свойство.Гидростатическое давление в любой точке жидкости не зависит от ориентировки площадки, на которую оно действует, т.е. гидростатическое давление действует одинаково по всем направлениям.
Для доказательства второго свойства выделим внутри жидкости бесконечно малый объем в форме тетраэдра с ребрами dx, dy, dz, параллельными координатным осям x, y, z (рис. 1.5).
Рис. 1.5. Второе свойство гидростатического давления
На тетраэдр действуют поверхностные силы - силы гидростатического давления Px, Py, Pz, Pn, направленные по нормали к соответствующим площадкам wх, wy, wz, wn и в соответствии с первым свойством гидростатического давления внутрь рассматриваемого объема жидкости (сжимающие). Кроме поверхностных действуют и массовые силы. Равнодействующую массовых сил, отнесенную к единице массы (единичную массовую силу), обозначим G, а ее проекции на оси координат - Gx, Gy, Gz. Условие равновесия выделенного элемента жидкости – сумма проекций всех сил на координатные оси – равна нулю (или, другими словами, равнодействующая всех сил равна нулю). Проекции внешних сил на оси координат будут равны:
Ввиду того что мы рассматриваем бесконечно малые площадки, давление в пределах одной грани тетраэдра можно считать постоянным. Тогда сила давления будет равна давлению, умноженному на площадь грани, т.е. dPx = pxdwx; dPy = pydwy; dPz = pndwz; dPn = pndwn. Рассмотрим проекцию силы dPn на ось x:
dPn cos(n^x) = pndwncos(n^x) = pxdwx . (1.17)
Так как ось x и ось n перпендикулярны к соответствующим площадкам dwx и dwn, то, следовательно, угол между площадками dwx и dwn будет равен углу между осями x и n (т.е. n^x). Аналогично формуле (1.17)
Масса элемента определяется как произведение плотности жидкости на объем тетраэдра:
С учетом того, что
запишем условия равновесия тетраэдра (1.16) в следующем виде:
Упростив уравнения, получим
Последние члены левых частей уравнений представляют собой произведения конечных величин (1/3rGx и т.д.) на бесконечно малые (dx и т.д.) и, значит, последние члены бесконечно малы и ими можно пренебречь. Тогда получим px - pn =0; py - pn = 0; pz - pn = 0 (1.22) или px = py = pz = pn . (1.23) Так как размеры тетраэдра dx, dy и dz были взяты произвольно, то и наклон площадки произволен, и, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково. Поскольку при выделении элементарного тетраэдра никаких ограничений относительно его положения в неподвижной жидкости не накладывалось, то из последнего соотношения (1.23) следует, что в покоящейся жидкости гидростатическое давление в любой точкене зависит от ориентации площадки, к которой приложено давление. Так как давление не зависит от ориентации площадки, проходящей через данную точку, и определяется только положением точки в жидкости, то давление является функцией только координат:
p = f (x,y,z) . (1.24) 4 Дифференциальные уравнения равновесия Эйлера Рассмотрим равновесие элементарного прямоугольного параллелепипеда со сторонами dx, dy, dz, выделенного внутри покоящейся жидкости (рис. 1.6).
Рис. 1.6. Элементарный объем жидкости
Предположим, что в точке А (центр тяжести параллелепипеда) действует гидростатическое давление p. Проведем через точку А горизонтальную линию MN, пересекающую грань 1-3-6-5 в точке М и грань 2-4-7-8 в точке N. С учетом непрерывности изменения давления в жидкости, т.е. функциональной зависимости, давление в точках М и N будет равно:
где Сила гидростатического давления на грань 1-3-6-5 направлена по оси х (1-е свойство), т.е. положительна:
а сила гидростатического давления на грань 2-4-7-8 направлена в обратную сторону, т.е. отрицательна:
Проекция массовых сил на ось х будет равна произведению Gxrdxdydz,гдеrdxdydz=dm - масса параллелепипеда, Gx - проекция единичной массовой силы на ось х. С учетом 1-го свойства гидростатического давления уравнение равновесия параллелепипеда в проекции на ось х будет иметь вид
откуда Учитывая 2-е свойство гидростатического давления, точно так же можно получить уравнения для проекций равнодействующей поверхностных и массовых сил на оси y и z:
Уравнения (1.27), (1.28) могут быть переписаны так:
Впервые эти уравнения были выведены членом Российской академии наук Л. Эйлером в 1755 г., и поэтому их называют уравнениями Эйлера. Если систему уравнений (1.29) умножим на dx, dy, dz и сложим, то получим:
или (1.30) Так как гидростатическое давление является лишь функцией координат точек х, y, z (1.24), то левая часть уравнения (1.30) представляет собой полный дифференциал и может быть обозначена через dp, т.е. dp = r(Gxdx + Gydy + Gzdz). (1.31) Система уравнений (1.29) или уравнение (1.31) позволяют описать закон распределения гидростатического давления в объеме жидкости. Поверхность, в каждой точке которой давление постоянно, называют поверхностью уровня. Для такой поверхности справедливы условия: p = const, dp = 0, тогда из формулы (1.31) следует: Gxdx + Gydy + Gzdz = 0. (1.32) Это и есть уравнение плоскости равных давлений. Отметим, что свободные поверхности жидкости (поверхности раздела газ – жидкость) являются поверхностями равного давления (уровня). 1.5. РАВНОВЕСИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ Будем полагать, что из массовых сил действуют только силы тяжести. Тогда составляющие массовой силы в направлении осей х и y равны нулю, т.е. Gx = 0, Gy = 0. Тогда из уравнений (1.29) при p = const следует:
Это может быть только в том случае, когда давление в плоскости xy постоянно, т.е. p (x,y) = const . (1.33)
Следовательно, поверхности равного давления - горизонтальные плоскости, проходящие через однородную жидкость. Определим величину проекции единичной массовой силы на ось z:
Знак минус в равенстве (1.34) обусловлен тем, что ось z направлена вертикально вверх, а сила тяжести вниз, т.е. в противоположную сторону. Учитывая, что p = f(z), а также равенство (1.34), уравнение можно записать так:
Разделяя переменные и интегрируя, получаем dp = - rgdz; (1.35) p = rgz + C, где C - постоянная интегрирования. Представим уравнение (1.35) в следующем виде:
Таким образом, в объеме однородной жидкости сумма величин z и Предположим, имеется объем однородной жидкости (рис. 1.7).
Рис. 1.7. Определение давления в точке, погруженной в жидкость на глубину h
Плоскость сравнения 0-0 служит началом отсчета координаты z. Эту плоскость можно выбирать на любом уровне, но для всех точек она должна быть одна и та же. В соответствии с основным уравнением гидростатики
Из основного уравнения гидростатики можно получить формулу для определения давления в точке жидкости, находящейся на глубине h от поверхности. Предположим над свободной поверхностью (см. рис. 1.7) давление p0, тогда:
Таким образом, давление в любой точке покоящейся жидкости равно внешнему давлению (т.е. давление на поверхность), сложенному с весом столба жидкости высотой от поверхности до данной точки и с площадью основания, равной единице. Из уравнения (1.37) следует, что при увеличении давления p0 на величину Dp для сохранения равенства левая часть уравнения, т.е. гидростатическое давление p в данной точке, также должна увеличиваться на Dp. Это справедливо для любой точки жидкости. Закон Паскаля.Изменение давления в какой-либо точке покоящейся жидкости, не нарушающее ее равновесия, передается в остальные точки без изменения. На использовании этого закона основана работа ряда гидравлических машин, наиболее распространенной из которых является гидравлический пресс. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 962. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

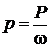 . (1.13)
. (1.13) (1.14)
(1.14) . (1.15)
. (1.15)
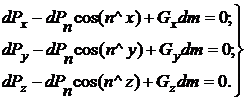 (1.16)
(1.16)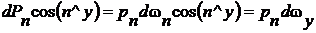 ;
; .
.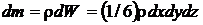 . (1.18)
. (1.18) ;
;  ;
;  , (1.19)
, (1.19) (1.20)
(1.20) (1.21)
(1.21)
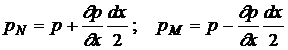 , (1.25)
, (1.25) - изменение давления на расстоянии
- изменение давления на расстоянии 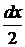 .
. ,
,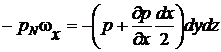 .
.
 , (1.26)
, (1.26)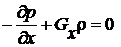 . (1.27)
. (1.27)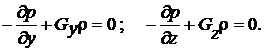 (1.28)
(1.28) . (1.29)
. (1.29)
 .
.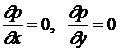 .
.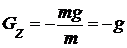 . (1.34)
. (1.34) .
. . (1.36)
. (1.36) в любой точке одна и та же. Полученное соотношение (1.36) называется основным уравнением гидростатики.
в любой точке одна и та же. Полученное соотношение (1.36) называется основным уравнением гидростатики.
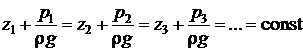 .
. (1.37)
(1.37)