
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Контрольной работы №11 для ЗРФСтр 1 из 7Следующая ⇒ Методические указания и задания К контрольным работам студентов III курса заочного отделения Для ЗРФ Составитель: Ваксман К.Г. Михайлова А.В.
Москва, 2006 г. Контрольная работа № 11 для ЗРФ Тема: Уравнения математической физики.
Краткие теоретические сведения.
1. Уравнения математической физики – это дифференциальные уравнения относительно функции двух или трех переменных и частных производных от нее второго и первого порядка, линейные относительно функции и ее частных производных. 1.1. Для однородных уравнений в частных производных (в которых отсутствует посторонняя функция в правой части уравнения) справедливо утверждение, что общее решение есть функциональный ряд, составленный из частных решений. 2. Решение уравнения теплопроводности в конечном стержне длиной 2.1. Искомая функция 2.2. Начальным 2.3. Граничным условиям
2.3.1.
2.3.2. 3. Решение уравнения теплопроводности будем искать методом Фурье разделения переменных. Пусть частные решения представлены в виде произведения двух функций, каждая их которых зависит только от одной независимой переменной. 3.1. Тогда Подставим в (2.1) Разделим обе части уравнения на Обе части этого уравнения должны быть постоянными, т.к. левая часть не зависит от  3.2.1.
3.2.2. Решим 3.2.1. Поскольку температура Решим уравнение 3.2.2. Решение 3.2.2. Из второго граничного условия 2.3.2. Числа 3.2.3. 3.2.4. Частное решение 4. Общее решение уравнения теплопроводности (по 1.1.) 5. Необходимо определить коэффициенты
5.1.) 5.1.1. Решение примера задания Контрольной работы № 11 для ЗРФ Найти решение уравнения теплопроводности. (I) Начальные условия: (II) Граничные условия: (III) Решение: Пусть Подставим в уравнение (I) Получим два обыкновенных дифференциальных уравнения а) Решим уравнение а) Решим уравнение б) Характеристическое уравнение Воспользуемся граничными условиями (III) По 3.2.3 По 3.2.4 Общее решение по 4) Найдем По 5.1.1 Для получения А) Напомним, а) они вычисляются методом интегрирования по частям: если б) в) Вычислим А) В) При вычислении Итак, решение
Варианты заданий контрольной работы №11 для ЗРФ Тема: Уравнения математической физики. Задание: Найти решение уравнения теплопроводности на отрезке а) начальным условиям б) граничным условиям
Контрольная работа № 12 для ЗРФ Тема: «Элементы теории функций комплексного переменного» Краткие теоретические сведения. 1. Комплексное число Запись: 1.1. Комплексное число 1.2. Тригонометрическая форма комплексного числа 1.3. Показательная форма комплексного числа 1.4. 1.5. Пусть 1.5.1 1.5.2 1.5.3 1.5.4 2. Функция комплексного переменного. Пусть Примеры: 1) 2) 3. Элементарные функции комплексного переменного. 3.1. Степенная функция Пусть 3.2. 3.3. Показательная функция. Пусть 3.4. Логарифмическая функция.
3.5. Тригонометрические функции. Пусть 4. Производная функция комплексного переменного. 4.1. Пусть
4.2. Если 4.3. Необходимые и достаточные условия аналитичности функции 4.4. Для нахождения производной 5. Ряд Лорана для функции 5.1. или 5.2. Приёмы разложения функции в ряд Лорана в окрестности точки 5.2.1. Используют разложение в ряд Маклорена основных элементарных функций, беря 5.2.2. Если надо получить разложение функции 1) внутри круга с центром в точке b, радиуса
2) вне круга с центром в точке b, радиуса
5.2.3. Разложения для 5.2.4. Часто надо предварительно преобразовать разлагаемую в ряд функцию, применив формулы:
5.2.5. Рациональную дробь надо представить в виде суммы простейших дробей
Примеры выполнения заданий |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 213. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
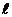 .
. или
или  .
.
 – температура в точке с координатой
– температура в точке с координатой 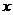 бесконечно тонкого стержня в момент времени
бесконечно тонкого стержня в момент времени 
 .
.  – постоянный коэффициент. Функция
– постоянный коэффициент. Функция  – т.е. значение температуры в начальный момент времени в точках стержня равно
– т.е. значение температуры в начальный момент времени в точках стержня равно  .
.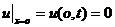
 , т.е. температура на концах стержня равна нулю.
, т.е. температура на концах стержня равна нулю.
 а
а 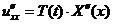 .
. .
.  ;
;  .
.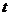 , т.е. они не зависят ни от
, т.е. они не зависят ни от  . Получим два обыкновенных дифференциальных уравнения.
. Получим два обыкновенных дифференциальных уравнения. .
. .
.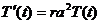 или
или 
 не может ни при каком
не может ни при каком 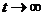 , то
, то 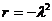 ;
;  .
. или
или  Это линейное уравнение с постоянными коэффициентами. Характеристическое уравнение
Это линейное уравнение с постоянными коэффициентами. Характеристическое уравнение 

 . Из первого граничного условия 2.3.1.
. Из первого граничного условия 2.3.1.  следует, что
следует, что  т.е.
т.е.  а
а  , т.е.
, т.е.  .
. следует, что
следует, что 
 т.к.
т.к. 
 , где
, где 
 , зависящие от натурального числа
, зависящие от натурального числа  , называются собственными числами задачи.
, называются собственными числами задачи.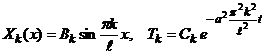 .
.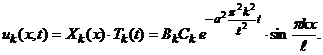 Обозначим произведение произвольных постоянных
Обозначим произведение произвольных постоянных 
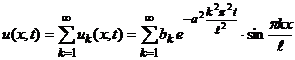 .
. , пользуясь начальным условием 2.2.
, пользуясь начальным условием 2.2. Учтя, что
Учтя, что 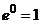 , получим
, получим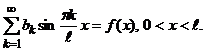 5.1. – это разложение функции
5.1. – это разложение функции  , заданной на интервале
, заданной на интервале  , в ряд Фурье по синусам. Коэффициенты
, в ряд Фурье по синусам. Коэффициенты  . Подставив вычисленные
. Подставив вычисленные  , 0<
, 0<  .
.
 .
.  .
.  ,
, 
 ;
;  ,
,  .
. ;
;  .
. ; б)
; б)  .
. ,
,  ,
, 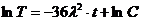 .
.
 ,
,  ;
;  ,
,  .
.
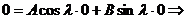





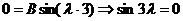 ;
; 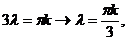

 и
и  .
. .
.
 .
. , воспользовавшись начальными условиями (II)
, воспользовавшись начальными условиями (II) 
 .
. .
.  , В)
, В)  .
.
 , то
, то 
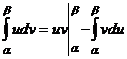
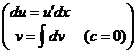 ;
; ;
;  ;
; , где
, где  (
( 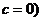 .
.


 .
.
 .
. ,
,  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;

 .
. .
. ,
,  ;
;  ,
,  удовлетворяет:
удовлетворяет: ;
;
 .
.
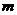











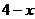






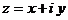 . i – мнимая единица,
. i – мнимая единица,  , т.е.
, т.е.  . х, у – любые действительные числа; х – действительная часть, а у – мнимая часть комплексного числа.
. х, у – любые действительные числа; х – действительная часть, а у – мнимая часть комплексного числа. .
. плоскости хоу (комплексной плоскости z).
плоскости хоу (комплексной плоскости z). , где
, где  – модуль,
– модуль,  .
.  – аргумент комплексного числа z.
– аргумент комплексного числа z. 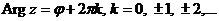 .
.  .
. .
. и т.д.
и т.д.  .
. .
.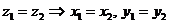 .
.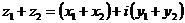 .
. .
. .
. может быть представлена в виде двух действительных функций u и v от действительных переменных х и у.
может быть представлена в виде двух действительных функций u и v от действительных переменных х и у.  ,
,  .
. , тогда
, тогда  ;
;
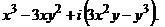
 .
. , n – целое, положительное число.
, n – целое, положительное число.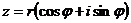 , тогда
, тогда  .
. – корень целой положительной степени, если
– корень целой положительной степени, если  – n-значная функция при
– n-значная функция при  .
. .
.
 .
.  – бесконечнозначная функция.
– бесконечнозначная функция. .
. , где
, где 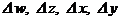 – приращения.
– приращения. имеет производную во всех точках области D, то
имеет производную во всех точках области D, то  , где
, где  и
и 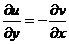 .
. применяются обычные правила дифференцирования.
применяются обычные правила дифференцирования.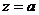 имеет вид.
имеет вид.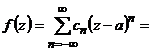

 .
.
 в окрестности
в окрестности  , то надо представить функцию
, то надо представить функцию 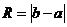 .
. , можно воспользоваться табличным рядом Маклорена (6) для
, можно воспользоваться табличным рядом Маклорена (6) для  при
при  .
. , можно воспользоваться табличным рядом Маклорена (6) для
, можно воспользоваться табличным рядом Маклорена (6) для  при
при  , т.е.
, т.е.  .
. можно получить продифференцировав ряд для
можно получить продифференцировав ряд для  , т.к.
, т.к.  .
. ;
;  ;
;  . Например, если надо разложить
. Например, если надо разложить 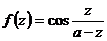 в окрестности
в окрестности 
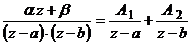 . А1 и А2 получим, приведя правую часть тождества к общему знаменателю и приравняв числители дробей слева и справа.
. А1 и А2 получим, приведя правую часть тождества к общему знаменателю и приравняв числители дробей слева и справа. . Получим систему уравнений относительно А1 и А2
. Получим систему уравнений относительно А1 и А2  .
.