
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формулы прямолинейного равноускоренного движения.Если тело (материальная точка) движется вдоль оси х с постоянным ускорением, проекция которого на эту ось равна
Проекция
Формулы равноускоренного движения используются при решении задач на падение тел вблизи поверхности Земли, т.к. такое движение происходит под действием силы тяжести с постоянным ускорением Поступательное движение тела. Поступательным называется движение, при котором любая прямая, проведенная в теле, перемещается параллельно самой себе. Т.к. при поступательном движении траектории, скорости и ускорения всех точек тела совпадают, то для описания движения тела достаточно рассмотреть движение любой его точки.
КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой – оси вращения.
Характеристики вращательного движения. а) Угловая скорость Быстрота вращения характеризуется угловой скоростью
При равномерном вращении его быстроту также описывают частотой оборотов 
Период вращения
то
б) Угловое ускорение Угловое ускорение
Рисунок 3 – Направление угловой скорости
Векторы
2. Связь линейных и угловых характеристик. Если точка тела отстоит от оси вращения на расстоянии
Скорость точки
При вращении тела тангенциальное ускорение его точки
Нормальное ускорение точки тела
Полное ускорение, как указывалось ранее, определяют по формуле
Формулы равноускоренного вращения. Если угловое ускорение
ДИНАМИКА ЗАКОНЫ НЬЮТОНА В основе классической механики лежат законы Ньютона. 1-й закон: если сумма сил, действующих на тело, равна нулю ( 2-й закон: произведение массы
3-й закон: с какой силой первое тело действует на второе, с такой же по величине и обратной по направлению силой второе тело действует на первое. Системы отсчета, в которых справедливы законы Ньютона, называются инерциальными.
СИЛЫ В МЕХАНИКЕ
Гравитационная сила. Две точечные массы
2. Сила тяжести. Силой тяжести тела массой
Вследствие суточного вращения Земли и несферичности ее формы величина
На высоте
Вес тела. Вес представляет собой силу, с которой тело действует на горизонтальную опору или на подвес. По величине вес и сила тяжести совпадают только в том случае, если опора неподвижна. Например, вес тела, находящегося в движущемся вверх с ускорением лифте, превышает его силу тяжести. Сила трения. При скольжении тела действующая на него сила трения
Рисунок 4 – Силы, приложенные к телу, скользящему по плоскости под действием силы
Сила упругости. Сила упругости, действующая на тело со стороны деформированной (сжатой или растянутой) пружины, равна по величине
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 336. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
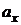 , то зависимость координаты тела
, то зависимость координаты тела 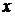 от времени
от времени 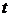 описывается уравнением
описывается уравнением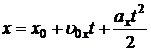 . (14)
. (14)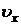 скорости в момент
скорости в момент 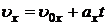 . (15)
. (15)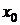 - начальная координата и
- начальная координата и 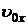 - проекция скорости на ось х в момент времени
- проекция скорости на ось х в момент времени 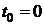 .
.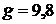 м/c2 (ускорение свободного падения тел).
м/c2 (ускорение свободного падения тел).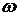 .
.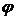 по времени
по времени 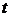
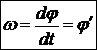 , (16)
, (16)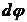 - угол поворота тела за малое время
- угол поворота тела за малое время 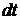 .
.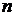 и периодом вращения
и периодом вращения 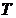 . Частота оборотов
. Частота оборотов 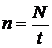 , (17)
, (17)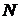 - число оборотов за время
- число оборотов за время 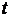 . Т.к. за один оборот тело поворачивается на угол, равный 2
. Т.к. за один оборот тело поворачивается на угол, равный 2 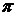 , то
, то 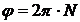 и
и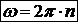 . (18)
. (18)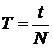 ,
,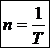 ,
, 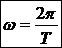 . (19)
. (19)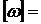 рад/с ,
рад/с , 
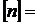 об/с ,
об/с , 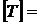 с .
с .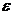 .
.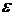 «эпсилон» равно производной от угловой скорости
«эпсилон» равно производной от угловой скорости 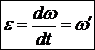 , (20)
, (20)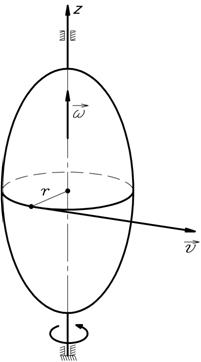
 - изменение угловой скорости за время
- изменение угловой скорости за время 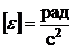 .
.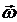 .
.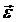 направлены по оси вращения тела; вектор угловой скорости
направлены по оси вращения тела; вектор угловой скорости 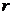 , то за время
, то за время 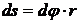 .
.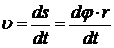 , или
, или 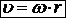 . (21)
. (21)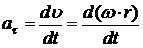 , или
, или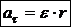 . (22)
. (22)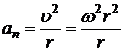 , или
, или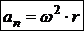 . (23)
. (23)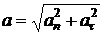 .
. 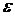 постоянно, то
постоянно, то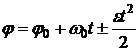 , (24)
, (24)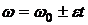 , (25)
, (25)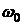 и
и 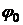 – угловая скорость и угол поворота тела в начальный момент
– угловая скорость и угол поворота тела в начальный момент 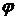 – в момент времени
– в момент времени 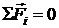 ), то тело или покоится, или движется прямолинейно и равномерно.
), то тело или покоится, или движется прямолинейно и равномерно.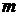 тела на его ускорение
тела на его ускорение 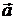 равно сумме сил, действующих на тело,
равно сумме сил, действующих на тело,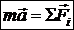 . (26)
. (26)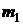 и
и 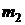 , расположенные на расстоянии
, расположенные на расстоянии 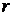 друг от друга, притягиваются с силой
друг от друга, притягиваются с силой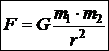 , (27)
, (27)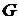 =6,67·10-11 м3/(кг·с2) – гравитационная постоянная. Уравнение (27) представляет собой закон всемирного тяготения.
=6,67·10-11 м3/(кг·с2) – гравитационная постоянная. Уравнение (27) представляет собой закон всемирного тяготения.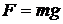 , (28)
, (28)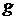 – ускорение свободного падения.
– ускорение свободного падения.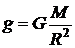 =9,8 м/с2 ,
=9,8 м/с2 ,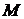 и
и 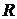 - масса и радиус Земли.
- масса и радиус Земли.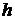 над поверхностью Земли
над поверхностью Земли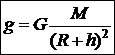 . (29)
. (29)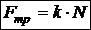 , (30)
, (30)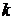 - коэффициент трения,
- коэффициент трения, 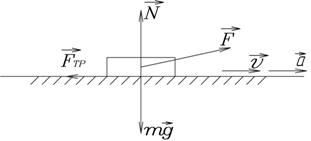
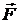 .
.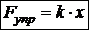 , (31)
, (31)