
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Последовательность расчётов при корреляционном анализеРассчитываются следующие показатели: r – коэффициент корреляции dу/х – коэффициент детерминации Sd –ошибка коэффициента корреляции tr факт.– критерий существенности (значимости) корреляции r – коэффициент корреляции служит для измерения силы (тесноты, степени) и направления линейной связи. Изменяется от -1 до +1. считается, что при: r = 0 линейная (прямолинейная) связь между изучаемыми признаками отсутствует (может быть, криволинейная связь). r = 0 – 0,3 – связь слабая r = 0,3 = 0,7 – связь средняя r = 0,7 = 1,0 – связь сильная (тесная) Для положительных (или прямых) связей, коэффициент корреляции (r), со знаком (+) будет означать, что с увеличением суммы осадков, увеличивается урожай. Для отрицательных (обратных) связей знак (-) означает, что при увеличении суммы осадков, снижается урожай. При полных связях , когда корреляционная связь превращается в функциональную, r – для прямых (положительных) связей равен (+1), а для обратных (отрицательных) связей равен (– 1) Чем ближе r к (+1) или к (-1), те сильнее (теснее) линейная (прямолинейная) корреляционная связь. . Коэффициент корреляции для выборочных наблюдений вычисляют по формул
Не вычисляя отклонения и квадраты отклонений, корреляцию можно рассчитать по формуле
где 2. Степень связи между признаками более точно измеряется коэффициентом детерминации  3. Коэффициент корреляции выборочных наблюдений подвержен случайным колебаниям, которые зависят как от особенностей образования выборки, так и от точности наблюдений. Поэтому для оценки надёжности
где С увеличением объёма выборки Критерий существенности коэффициента корреляции определяют по формуле Если При достаточно большом числе наблюдений (не менее 100) коэффициент корреляции считается существенным, если он превышает свою ошибку в три и более раза, т.е. когда
Регрессионный анализ При корреляционном анализе с помощью коэффициента корреляции можно выяснить тесноту (силу) и направление связи, но нельзя узнать, как количественно меняется результативный признак при изменении факториального на единицу измерения. Эта задача решается с помощью регрессионного анализа. Регрессия – это изменение результативного признака (зависимой переменной, или функции Y) при определённых изменениях факторного признака (независимой переменной или аргумента Х). Например, с изменением длины листа на 1 см его площадь изменяется на 4,6 см2. Различают регрессию простую и множественную, по форме – линейную и криволинейную. Сущность регрессионного анализа состоит в том, чтобы построить линию (прямую в случае прямолинейной зависимости), которая наиболее точно выражала бы зависимость одного признака от другого. Зависимость функции от аргумента при линейной регрессии выражается коэффициентом регрессии (в), который показывает, как в среднем изменяется (увеличивается или уменьшается, смотря по знаку в) результативный признак (функция) при изменении факториального признака (аргумента) на одну единицу измерения. Коэффициенты линейной регрессии вычисляются по формулам:
Коэффициенты регрессии имеют знак коэффициента корреляции. Произведение коэффициентов регрессии равно квадрату коэффициентов корреляции (что используется для проверки расчётов коэффициентов регрессии): Чаще всего из двух коэффициентов регрессии вычисляют только один. При исследовании односторонней зависимости, например корреляции между урожаем Y и количеством выпавших осадков Х (как в нашем примере), вычисляют только один коэффициент регрессии результативного признака Так с увеличением количества осадков во II и III декадах июня на 1 мм урожайность яровой пшеницы повысится на 0,34 ц/га. Вычисление
Критерий существенности коэффициента регрессии равен: Сопоставляя значения После корреляционных и регрессионных анализов составляют уравнени регрессии, которые используют: ü для вычисления неизвестного показателя по известному, например площади листьев по их длине; ü для прогнозирования будущего урожая по числу цветков или завязей; ü для прогнозирования качества урожая по элементам погоды; ü для прогнозирования распространения вредителей и болезней по внешним условиям; ü для прогнозирования качества продуктов переработки и их хранения по качеству сырья и т. д. Связь между функцией и аргументом выражается уравнением регрессии или корреляционным уравнениям. При простой регрессии уравнением кратко обозначается Y=f (x) и при множественной Y=f (X,Z,V…). Если степень связи между признаками велика, то по уравнению регрессии можно предсказать значение результативного признака для определенных значений факториальных признаков. Для оценки тесноты связи используют коэффициенты корреляции и корреляционное отношение. Совместное применение методов корреляции, регрессии и дисперсионного анализа для уточнения эксперимента получило название ковариационного анализа. Для наглядности корреляцию можно изобразить в виде линии регрессии. Теоретическую линию регрессии можно построить двумя способами: - графическим (с помощью прозрачной линейки), позволяющим приближённо выявить лишь общую тенденцию зависимости; - аналитическим, используя уравнение линейной регрессии Y по Х:
где Подставляя в это уравнение вычисленные значения Суть ковариационного анализа сводится к следующему. Если между результативным признаком Y и сопутствующим эксперименту не изучаемым признаком Х имеет место значимая линейная связь, то методом ковариации можно статистически выровнять условия проведения опыта в отношении признака Х и тем заметно снизить ошибку эксперимента и получить больше информации об изучаемом явлении.
Ковариационный анализ Ковариационный анализ– одновременный анализ сумм квадратов и сумм произведений отклонение двух или более переменных от их средних. Он используется при планировании и статистической обработке результатов опыта как способ уменьшения ошибки эксперимента, не поддающейся непосредственному контролю (выравниванию). Ковариационный анализ позволяет установить соотношение между вариацией зависимой переменой, например урожаев Y, и вариацией, сопутствующей эксперименту переменой Х, например исходным состоянием многолетних деревьев, густотой стояния растений, содержанием в почве питательных веществ и т.д. На основе соотношения проводится статистическое выравнивание условий эксперимента. Статистический контроль над сопутствующей опыту дает возможность получить такой конечный результат, который был бы получен при сохранении величины Х на постоянном уровне. Это заметно уточняет результаты опыта, снижает его ошибку. В узком смысле под ковариацией, обозначаемой cov или sxy в математической статистике понимается среднее произведение отклонений двух переменных от их средних. Ковариация может быть как положительной, так и отрицательной. В более широком смысле ковариацией называют совокупность трех статистических показателей: средних арифметических х и у, сумм квадратов варьирования и состовляет суть ковариационного анализа. Ковариационный анализ включает три основных этапа: С дисперсионный анализ ряда X,Y и произведений XY; В разложение остаточной дисперсии Сz по ряду Y (остаток I) на сумму квадратов отклонений, обусловленную регрессией Y по X, обозначаемую Сb , и сумму квадратов отклонений от регрессии Cd y×x (остаток II); Сz (остаток I) = Cb + Cd y×x (остаток II); В приведение фактических средних по ряду Y к полной выравненности условий эксперимента по ряду сопутствующей переменной Х. Таким образом, ковариационный анализ – это распространение методов дисперсионного анализа на случай нескольких переменных, а так же корреляционного и регрессионного анализов на общие схемы полевых, вегетационных и лабораторных экспериментов. Когда между переменной Y, подлежащей изучению, и сопутствующей переменной Х можно предполагать линейную связь, то целесообразно запланировать измерение величины Х. Это дает возможность получить дополнительную информацию об изучаемом явлении и использовать регрессию в целях уточнения эксперимента. Выравнивают обычно только итоговые данные, т.е. средние, поэтому в уравнении регрессии Y и X будут соответствовать средним по вариантам опыта. В агрономических исследованиях ковариационный анализ целесообразно использовать для уточнения опыта в двух основных случаях:
1) если на результативный признак может оказать заметное влияние разное исходное состояние условий эксперимента - плодородие почвы, мощность многолетних растений и т.п., которые могут быть измерены в начале опыта; 2) если на изучаемы признак в процессе эксперимента оказывают влияние не зависящие от вариантов опыта причины-выпадения растений и повреждения их болезнями, вредителями, птицами и т.д. Правильное применение ковариационного анализа предполагает независимое от вариантов опыта распределение случайной величины Х. Если сопутствующая Х имеет отношение к изучаемым вариантам, то исключение части эффекта неправомерно, так как это ведет к исключению части эффекта варианта.
Основные этапы планирования исследования (эксперимента)
Планирование – это определение задачи и объектов (растений) исследования, разработка схемы эксперимента, выбор земельного участка и оптимальной структуры опыта. Ошибки, допущенные при планировании, нельзя исправить в последующем ни тщательным проведением опытной работы, ни применением дорогостоящих инструментальных методов исследования и статистической обработки на современных ЭВМ. Период планирования включает: 1) выбор темы, определение задачи и объекта исследования; 2) определение актуальности исследований; 3) формулировку целей и задач исследований; 4) выбор объекта или объектов исследований; • 5) сбор и критический анализ имеющейся информации относительно исследуемой проблемы (изучение современного состояния вопроса); 3) выдвижение рабочей гипотезы или ряда конкурирующих гипотез (теоретических моделей); 4) разработку схемы и методики эксперимента. К теме предъявляют ряд требований: 1) Актуальность, критерия для установления степени актуальности пока нет, более актуальной считают ту тему, работа над которой дает больший экономический эффект; 2) Новизна темы – означает, что тема в данной постановке никогда не разрабатывалась и в настоящее время не разрабатывается; 3) Тема должна быть экономически эффективной и значимой – исследования должны давать экономический эффект, который определяется уже на стадии выбора темы; 4) Важная характеристика темы – реальность внедрения результатов исследований. Необходимо четко сформулировать цель исследования, построить логическую модель изучаемого явления и правильно выбрать стратегию, которая определяет методы и приемы исследования. Следующий этап планирования – изучение литературы по избранной проблеме и выдвижение рабочей гипотезы или ряда конкурирующих гипотез. Рабочая гипотеза служит отправным пунктом для составления схемы или ряда схем будущих опытов и разработки программы исследования. В программе указывают схемы опытов, основные элементы методики и техники эксперимента, наблюдения и учеты. Сложным и ответственным этапом планирования является разработка схемы и методики опыта, выбор полевых и лабораторных наблюдений (анализов) и учетов для оценки и объяснения действия изучаемых факторов. Надежность результатов эксперимента и соответствие их поставленной задаче зависят от правильного решения основного вопроса планирования. Главная задача любого эксперимента – это практическое решение какой-либо общей проблемы, неразрешенной на сегодняшний день (обеспечение населения продовольствием, экологическая безопасность и др.) или частной проблемы. В земледелии частными проблемами являются: увеличение продукции растениеводства, защита растений от сорняков, вредителей и болезней, повышение плодородия почвы и др. Тема исследования – это отдельный вопрос проблемы, решающий практические вопросы сельскохозяйственного производства, в конкретных почвенно-климатических условиях, для последующего широкого внедрения научных исследований в производство. При подготовке и проведении исследования можно выделить 3 этапа.
a) выбор темы исследования и её обоснование. Она должна быть актуальной и отвечать сегодняшнему дню. Она может быть прикладной (непосредственно для решения текущих задач) и теоретической (фундаментальные исследования). Без теоретических разработок, вероятен тупик в практике; b) определение цели и задач исследования Цель – одна (возможно две), задач может быть несколько и их нельзя путать; c) постановка рабочей гипотезы. Рабочая гипотеза – это научное предвидение (предположение), которое берётся за основу при объяснении ожидаемых в опыте результатов. 2. Составление программы и методики исследования(решение вопросов, что делать и как делать) a) программа исследований – это перечень изучаемых в опыте вопросов. Какие наблюдения, измерения, учёты и анализы в отношении почвы или растения будут проводиться в опыте.(что делать?); b) методы исследования. Это перечень методик при изучении поставленных вопросов (как делать) (пример, методика определения влажности почвы). Эти два этапа охватывают планирование эксперимента (мероприятия, проведённые до закладки опыта). |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 355. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 ,
,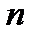 – число сопоставляемых пар (объём выборки).
– число сопоставляемых пар (объём выборки). , равным квадрату коэффициента корреляции (
, равным квадрату коэффициента корреляции (  ) и показывающим долю тех изменений (%), которые зависят от изучаемого фактора. При
) и показывающим долю тех изменений (%), которые зависят от изучаемого фактора. При  =0,8 не 80 %, а только 64 % изменчивости признака У обусловлена действием факториального признака Х (
=0,8 не 80 %, а только 64 % изменчивости признака У обусловлена действием факториального признака Х ( 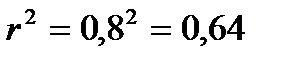 ), остальная часть корреляционной связи (
), остальная часть корреляционной связи (  ) обусловлена другими факторами.
) обусловлена другими факторами. определяют его ошибку
определяют его ошибку  и критерий существенности
и критерий существенности  :
: ;
;  – ошибка коэффициента корреляции;
– ошибка коэффициента корреляции; – число сопоставляемых пар (объём выборки).
– число сопоставляемых пар (объём выборки). уменьшается, а точность определения
уменьшается, а точность определения  возрастает.
возрастает.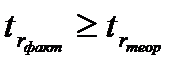 , то корреляционная связь существенна, а при
, то корреляционная связь существенна, а при 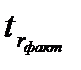 <
<  – несущественна.
– несущественна.  находят по табл. приложения 2 для 5%-ного, а при более строгом подходе – 1% - ного уровня значимости. Число степеней свободы принимают равным v
находят по табл. приложения 2 для 5%-ного, а при более строгом подходе – 1% - ного уровня значимости. Число степеней свободы принимают равным v  .
. .
. и
и  .
. ;
;  , который показывает, как изменяется Y при изменении Х на единицу измерения; выражается он в единицах Y.
, который показывает, как изменяется Y при изменении Х на единицу измерения; выражается он в единицах Y. лишено смысла, мы его рассчитали для проверки вычислений коэффициентов регрессии. Затем находят ошибку коэффициента регрессии:
лишено смысла, мы его рассчитали для проверки вычислений коэффициентов регрессии. Затем находят ошибку коэффициента регрессии:
 .
.

 и
и  мы не вычисляем, так как в данном примере
мы не вычисляем, так как в данном примере  , что свидетельствует о существенности регрессии.
, что свидетельствует о существенности регрессии. и
и  можно при заданном уровне значимости (05 или 01) и числе степеней свободы v
можно при заданном уровне значимости (05 или 01) и числе степеней свободы v  оценить существенность коэффициента регрессии результативного признака –
оценить существенность коэффициента регрессии результативного признака – 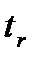 и значимость его доказана, то существенным будет и коэффициент регрессии, так как
и значимость его доказана, то существенным будет и коэффициент регрессии, так как 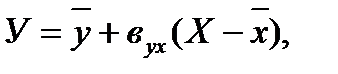
 и
и  – средние арифметические признаков Х и Y;
– средние арифметические признаков Х и Y; ;
;