
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дробный метод обработки данныхЭтот метод применяется для обработки результатов вегетационного опыта, в котором отсутствует связь между сравниваемыми вариантами – сосудами, а также полевых и лабораторных опытов, когда ошибки средних арифметических вычисляются на основании большого числа наблюдений (n = 20–30). Метод может в отдельных случаях применяться для обработки результатов полевого опыта (при отсутствии систематических ошибок). В опыте, проведённом по схеме: 1. Зяблевая вспашка на 20 – 22 см (контроль) 2. Осенняя плоскорезная обработка на 20 – 22 см 3. Осенняя плоскорезная обработка на 10 – 12 см 4. Весеннее лущение жнивья на 10 -12 см Получены следующие данные по урожайности: Обработку данных дробным методом проводят в следующей последовательности: 1.Составляют таблицу урожаев и вычисляют среднюю арифметическую величину по каждому варианту ( 2. Находят отклонения поделяночных урожаев от среднего урожая по варианту ( 3. Находят квадраты отклонений 4. Рассчитывают ошибки средних арифметических по вариантам. 5. Определяют разности между средними урожаями между контролем и опытными вариантами.
сравниваемых вариантов 6. Определяют ошибку разности между двумя средними (контролем и опытным вариантом).  Эта формула применяется для расчёта 7. Устанавливают существенность разности. Существенность различий между По экспериментальным данным вычисляем фактическое значение критерия ( Величина критерия t – показывает, во сколько раз разность (d) больше ошибки разности (Sd) Значение tтеор.- находят в приложении рабочей тетради при 5% или 1% уровне значимости и числе степеней свободы υ = n1 + n2 – 2 В нашем примере при Р = 5% и υ = 4 + 4 – 2 = 6 tтеор = 2,4 Разность При tфакт ≤ tтеор. разность между средними не выходит за пределы случайных колебаний т.е. считается несущественной. Так в нашем примере разница между вариантом с осенней плоскорезной обработкой на 20-22 см и вариантом с осенней вспашкой на 20-22 см в 2,0 ц/га будет существенной, т.к. При достаточно большом числе наблюдений ( Несмотря на свою простоту, дробный метод имеет некоторые недостатки: - для оценки существенности разности используется отвлечённые показатели ( - для каждого варианта в отдельности рассчитываются ошибка выборочной средней и ошибка разности, что увеличивает расчёты.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 429. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. –
– 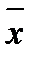 ). Правильность вычислений проверяют по равенству
). Правильность вычислений проверяют по равенству  (если
(если  и их суммы по каждому варианту в отдельности
и их суммы по каждому варианту в отдельности 

 где d – разность;
где d – разность; 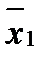 и
и  – средние арифметические
– средние арифметические где Sd – ошибка разности
где Sd – ошибка разности и
и 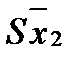 – ошибки сравниваемых вариантов
– ошибки сравниваемых вариантов при условии, что
при условии, что 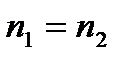 , и в случае, когда ошибки средних арифметических вычислены при большом числе наблюдений (n >20);
, и в случае, когда ошибки средних арифметических вычислены при большом числе наблюдений (n >20);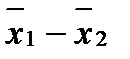 ) к её ошибке Sd. Это отношение и называется критерием существенности разности или критерием Стьютента ( tфакт ).
) к её ошибке Sd. Это отношение и называется критерием существенности разности или критерием Стьютента ( tфакт ).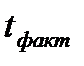 ):
): =
= 
 . Разница между вариантом с осенней плоскорезной обработкой на 10-12 см и контролем также существенна (
. Разница между вариантом с осенней плоскорезной обработкой на 10-12 см и контролем также существенна (  =4,6 >
=4,6 >  =2,4). Четвёртый вариант (без осенней обработки) не дал существенной прибавки урожая по сравнению с контролем.
=2,4). Четвёртый вариант (без осенней обработки) не дал существенной прибавки урожая по сравнению с контролем.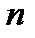 >20-30) разность
>20-30) разность  обычно считается существенной при уровне значимости 5%, если
обычно считается существенной при уровне значимости 5%, если  ≥ 2, а при уровне значимости 1% при
≥ 2, а при уровне значимости 1% при 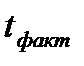 ≥ 3. Если
≥ 3. Если