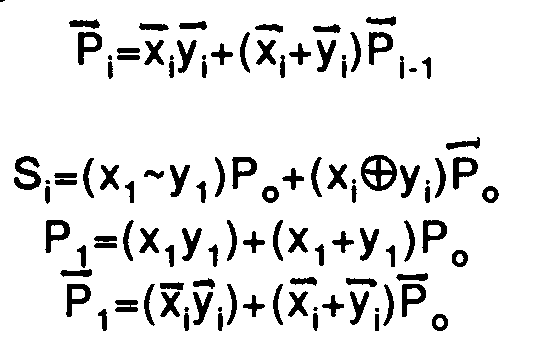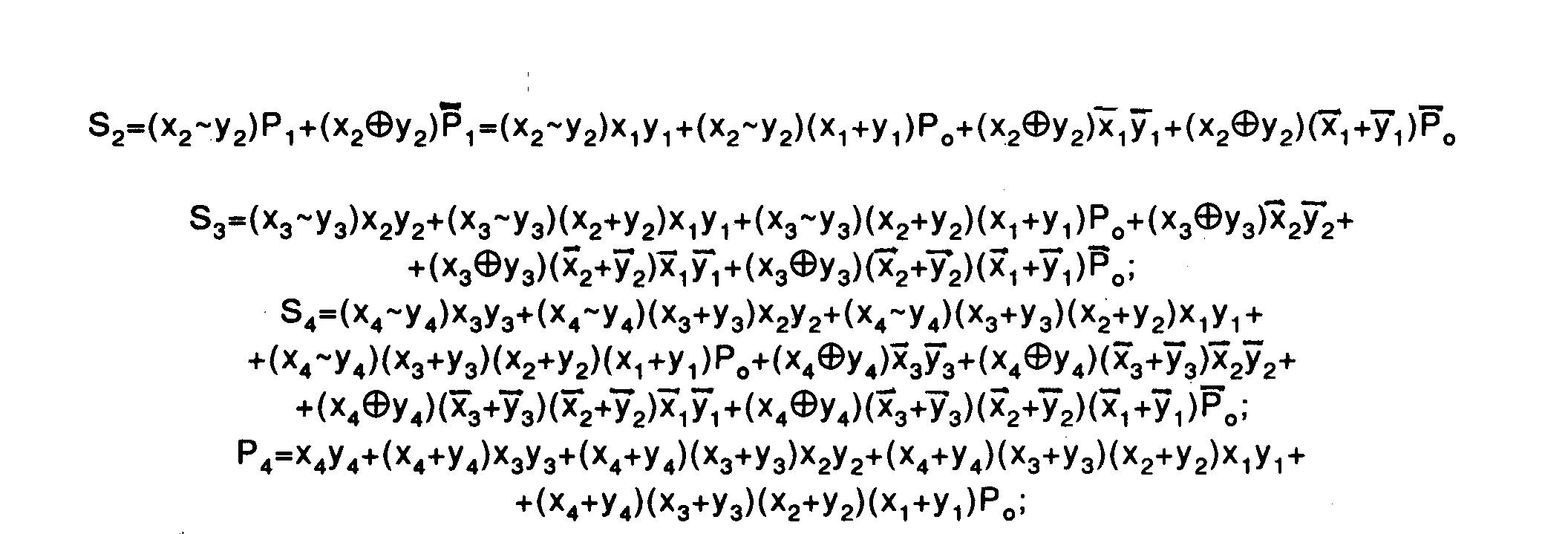Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГЛИН со стабилизатором токаВ отличие от рассмотренных выше схем в стабилизатор тока вводится обратная связь не по напряжению, а по току, что позволяет повысить внутреннее сопротивление стабилизатора. Эквивалентная схема ГЛИН (рис. 18) содержит идеальный источник тока /, параллельно которому включено внутреннее сопротивление переменному току R. В ГЛИН со стабилизатором тока можно получить малые коэффициенты нелинейности. Практическая схема ГЛИН со стабилизатором тока на транзисторе VT показана на рис. 19. Конденсатор С заряжается коллекторным током транзистора. Отрицательная обратная связь по току создается за счет сопротивления Rэ. При большой глубине обратной связи, внутреннее сопротивление стабилизатора Ri будет определяться выходной проводимостью транзистора в схеме "общая база" и может достигать значений 106 - 108. Общий недостаток схем ГЛИН со стабилизатором тока - плохая нагрузочная способность, поскольку сопротивление нагрузки оказывается включенным параллельно Ri и увеличивает коэффициент нелинейности
26. Триггер Шмидта на ОУ.
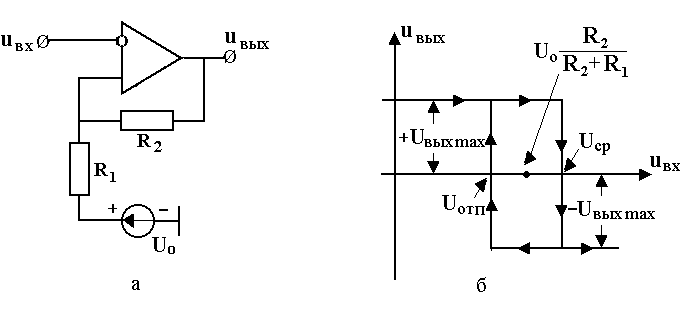
Наряду с простейшей схемой компаратора широко используется схема на ОУ с положительной обратной связью, называемая триггером Шмитта. Охват ОУ петлей положительной обратной связи и его работа в режиме насыщения, когда выходное напряжение может принимать только два значения (+Uвых max и -Uвых max) приводят к появлению на передаточной характеристике триггера Шмитта петли гистерезиса и двух значений напряжения входного сигнала, в которых происходит опрокидывание схемы. В схеме, приведенной на рис. 5.4,а, входное напряжение подается на инвертирующий вход ОУ. Опорным в этой схеме служит сумма напряжений, подаваемых на неинвертирующий вход с выхода ОУ через делительную цепочку резисторов R 
Рисунок 5.4. Триггер Шмитта при подаче входного напряжения на инвертирующий вход ОУ (U0 > 0): а – схема триггера, б – его передаточная характеристика Величина опорного напряжения в схеме рис. 5.4,а может быть определена с использованием принципа суперпозиции. Компонента этого напряжения, поступающая с выхода ОУ, определяется при условии, что напряжение дополнительного источника равно нулю (U u При напряжении на выходе ОУ, равном +Uвых max, согласно соотношению (5.1) на неинвертирующий вход подается напряжение U которое называется напряжением срабатывания. При выходном напряжении, равном -Uвых max, на неинвертирующем входе ОУ напряжение равно U которое называется напряжением отпускания. Напряжения срабатывания и отпускания – это значения, при которых происходит опрокидывание триггера Шмитта со схемой на рис. 5.4.а. Передаточная характеристика триггера Шмитта со схемой рис. 5.4,а представлена на рис. 5.4,б. Ее ход может быть объяснен следующим образом. Пусть напряжение на выходе ОУ равно +Uвых max, что обеспечивается при величине входного напряжения меньше напряжения срабатывания. При повышении входного напряжения положительное напряжение Uвых max на выходе ОУ будет сохраняться до тех пор, пока напряжение u При обратном изменении входного напряжения, т.е. при его уменьшении, напряжение на выходе ОУ будет положительным лишь после того, как u Таким образом, передаточная характеристика триггера Шмитта имеет гистерезис, ширина которого при схеме рис. 5.4,а равна U а напряжение, равноудаленное от напряжения срабатывания и напряжения отпускания, т.е. соответствующее центру петли гистерезиса, Uцентр= U0 В схеме триггера Шмитта, приведенной на рис. 5.5,а, входное напряжение подается на неинвертирующий вход ОУ, а опорное – на инвертирующий. Кроме входного напряжения, на неинвертирующий вход подается напряжение с выхода ОУ через делительную цепочку, составленную из резисторов R uнвх = uвых
Рисунок 5.5. Триггер Шмитта при подаче входного напряжения на неинвертирующий вход ОУ (U0 < 0): а – схема триггера, б – его передаточная характеристика Соотношение для определения величин, при которых происходит опрокидывание схемы получается из уравнения (5.6) при учете условия uнвх =U0 и подстановки вместо напряжения uвых двух значений: +UВЫХ max и -UВЫХ max. При подстановке -UВЫХ max получается большая из этих двух величин, т.е. определяется напряжение срабатывания. Uср = а при подстановке +UВЫХ max определяется напряжение отпускания Uотп = На рис. 5.5,б приведена передаточная характеристика триггера Шмитта со схемой рис. 5.5,а, которая имеет петлю гистерезиса. Изменение полярности напряжения на выходе триггера с отрицательного на положительное происходит при приближении uвх к напряжению срабатывания, когда выходное напряжение отрицательное. При приближении uвх к напряжению отпускания, когда на выходе триггера Шмитта положительное напряжение, т.е. с противоположной стороны, происходит изменение полярности выходного напряжения с положительной на отрицательную. Ширина петли гистерезиса определяется как: Uср- Uотп = а ее центр Uцентр= U0 Таким образом, согласно (5.5) и (5.10) смещение петли гистерезиса передаточной характеристики триггера Шмитта осуществляется изменением напряжения источника U0, аналога источника опорного напряжения в компараторе.
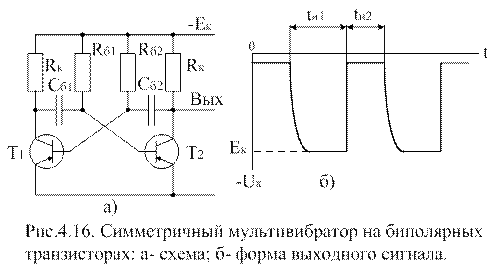
Рисунок 5.6. Временные диаграммы, иллюстрирующие переключения триггера Шмитта при многократных небольших изменениях контролируемого напряжения Использование триггера Шмитта придает системам автоматического регулирования и защиты новое свойство. Действительно, при применении простейшей схемы компаратора величина напряжения, при которой срабатывают эти системы, остается одинаковой вне зависимости от того, в какую сторону изменяется величина контролируемого напряжения. При применении триггера Шмитта срабатывание систем автоматического регулирования или релейной защиты будет происходить при превышении контролируемым напряжением величины U В схемах компаратора и триггера Шмитта при переключении происходит резкое изменение режима работы с ОУ. В таких условиях работы важно быстродействие ОУ, которое характеризуется задержкой срабатывания (временем задержки момента изменения выходного напряжения) и временем нарастания выходного напряжения. Для работы в импульсном режиме выпускаются специальные ОУ, у которых время срабатывания составляет единицы микросекунд, а время нарастания выходного напряжения – доли микросекунды. 27. Мультивибратор и одновибратор. Мультивибратор — это релаксационный (т.е. использующий положительную обратную связь) генератор прямоугольных импульсов. Он преобразует энергию источника питания в энергию выходных сигналов. Мультивибратор обладает свойством самовозбуждения. Простейшая схема мультивибратора, представленная на рис. 4.16, содержит два транзисторных ключа с симметричными коллекторно-базовыми обратными связями через конденсаторы. Базовые резисторы обеспечивают надежное открывание ключа:
где S — коэффициент запаса по насыщению.
Амплитуда выходного сигнала ненагруженного мультивибратора близка к напряжению питания
Длительности генерируемых импульсов определяются постоянной времени перезаряда конденсатора через базовый резистор:
При Скважность колебаний (при разных tU1 и tU2) ограничивается временем полного заряда конденсатора. При использовании транзисторов с коэффициентом усиления по току b = 30 можно получить значение скважности не более 10. Для того, чтобы мультивибратор начинит генерировать сразу при включении питания, должен быть мягкий режим самовозбуждения с минимальным запасом по насыщению. При глубоком насыщении возникает жесткое самовозбуждение, требующее внешнего воздействия для начала генерации. Без этого воздействия оба транзистора оказываются в открытом состоянии. Обычно используются мультивибраторы с S = 2–3. Меньшие значения S ухудшат прямоугольность выходного сигнала, а большие приведут к срыву генерации. Для улучшения формы генерируемых импульсов используют специальные схемы.
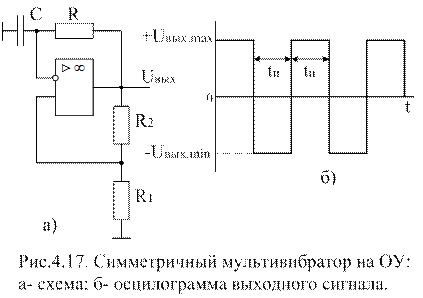
Симметричный мультивибратор на операционном усилителе показан на рис. 4.17. Он выполняется на базе инвертирующего триггера Шмитта, в котором отрицательная обратная связь включается через фильтр низкой частоты в виде RC-цепи. Длительность генерируемого импульса
Соответственно, частота генерации:
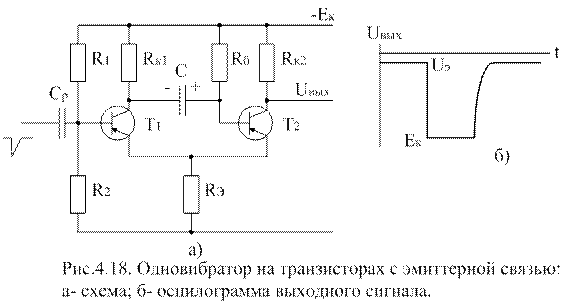
При Одновибратор — это схема с одним устойчивым состоянием и одним неустойчивым состоянием. Переход во второе состояние происходит под воздействием внешнего сигнала — запускающим импульсом. Время нахождения в этом состоянии зависит от параметров схемы и не зависит от длительности входного импульса. Таким образом, одновибратор является формирователем прямоугольного импульса заданной длительности. Быстродействие одновибратора определяется временем восстановления, после истечения которого устройство готово к приему следующего импульса. В случае реализации на транзисторах, одновибратор выполняется по схеме эмиттерной связи — рис. 4.18.
В исходном состоянии транзистор Т2 насыщен, а Т1 — заперт напряжением автоматического смещения, выделяемым на транзисторе R, от прохождения тока Iк2. Длительность входного импульса
Одновибратор можно запустить путем подачи отрицательного (открывающего) импульса на базу закрытого транзистора Т1 или положительного (запирающего) импульса на базу открытого транзистора Т2. Полярность указана применительно к использованным в схеме по рис. 4.18 транзисторам p-n-p типа. Следует иметь в виду, по выходное напряжение такого одновибратора содержит значительную потенциальную помеху, равную величине Uэ2 падения напряжения на резисторе Rэ от тока Iэ2. Амплитуда импульса на выходе одновибратора:
28. Логические элементы: определения, обозначения; логические функции. Логические операции реализуются с использованием электрических схем, которые называются логическими элементами. Они изготавливаются в виде интегральных микросхем в большинстве своем на базе диодов и транзисторов, либо только транзисторов. В связи с этим различают два типа логических элементов: ДТЛ (диодно-транзисторная логика) и ТТЛ (транзисторно-транзисторная логика). На рис. 7.2 представлены схемные обозначения элементов, выполняющих простейшие логические операции. При этом элементы “ИЛИ” и “И” – двухвходовые, т.е. выполняющие операции с двумя входными переменными. Однако промышленностью выпускаются логические элементы “ИЛИ” и “И” с большим числом входных клемм.
Рисунок 7.2. Схемное обозначение логических элементов На рис. 7.3 приведена схема на диодах, с помощью которой реализуется операция логического сложения. Действительно, при отсутствии на входах этой схемы сигналов (x
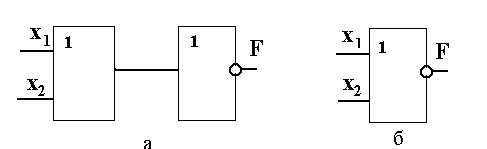
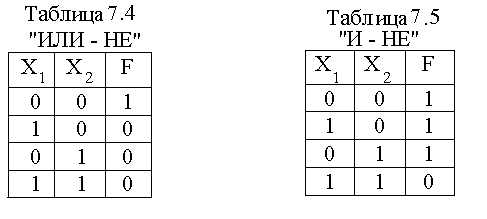
Рисунок 7.3. Реализация Рисунок 7.4. Реализация логической операции «И» на диодах «ИЛИ» на диодах Нетрудно также показать, что схема на рис. 7.4 обеспечивает выполнение операции “И”. Через резистор R Операция “НЕ” может быть реализована на биполярном транзисторе типа n-p-n, включенного по параллельному варианту построения ключевой схемы (рис. 4.2.а). Как было показано в разделе 4.1, при подаче на вход схемы сигнала положительной полярности определенного уровня(x = 1) транзистор будет находиться в открытом состоянии, т.е. в точке “б” на рис. 4.4,б. Этому режиму транзистора соответствует очень малая величина напряжения коллектор-эмиттер, ΔUКЭ ОТК, которая является выходом схемы,F = 0. При отсутствии на входе сигнала(x = 0)транзистор будет закрыт (точка «а» на рис. 4.4,в), и с выхода схемы снимается напряжение, практически равное+Е, т.е. F = 1. Следует отметить, что напряжение на выходе схем рис.7.3 и 7.4, равное нулю, обеспечиваются лишь при идеальном шунтировании резистора, с которого снимается выходное напряжение открытыми диодами. При реализации логической операции «НЕ» из-за наличия остаточного напряжения на открытом транзисторе выходное напряжение также отличается от нуля. Таким образом, в реальных логических элементах логическим нулем, фактически, является не нулевое, а малая величина напряжения. В связи с этим в справочных данных обычно вместо «0» указывается «н» (низкий уровень напряжения) и соответственно вместо «1» указывается «в» (высокий уровень напряжения). Логические элементы выпускаются промышленностью в виде серий. Элементы каждой серии, выполняющие различные операции, могут сопрягаться в сложную схему логического устройства. Элементы серии создаются на базе основного элемента, который обычно выполняет операции “ИЛИ-НЕ” или “И-НЕ”. Математическая форма представления этих операций имеет вид: F = Схемы, реализующие операции “ИЛИ-НЕ” и “И-НЕ”, могут быть получены при последовательном соединении двух схем, выполняющих операции соответственно “ИЛИ”-“НЕ” и “И”-“НЕ”, что показано на рис. 7.5,а и 7.6,а для случая двухвходовых элементов. Схемные обозначения элементов “ИЛИ-НЕ” и “И-НЕ” представлены на рис. 7.5,б и 7.6,б, а таблицы истинности – в табл. 7.4 и 7.5.
Рисунок 7.5. Логическая операция «ИЛИ-НЕ»: а – принцип реализации операции, б - схемное обозначение логического элемента
Рисунок 7.6. Логическая операция «И-НЕ»: а – принцип реализации операции, б - схемное обозначение логического элемента
Рисунок 7.7. Реализация логической операции «И-НЕ» на транзисторах На рис. 7.7 представлена схема на транзисторах, реализующая логическую операцию “И-НЕ”. Особенностью этой схемы является использование многоэмиттерного транзистора Т
Рисунок 7.8. Схемы реализации логических операций на элементах «И-НЕ» а – операции «НЕ», б – операции «И», в - операции «ИЛИ» Логические элементы «ИЛИ-НЕ» и «И-НЕ» называют базовыми, поскольку схемы, составленные только из этих элементов одного типа, позволяют реализовывать простейшие логические операции. Это нетрудно доказать с использованием формул алгебры логики, например, на схемах, составленных из элементов «И-НЕ», которые приведены на рис. 7.8. На вход элемента схемы рис. 7.8,а подаются две одинаковых переменных x. Поэтому согласно тождествам (7.11) и (7.1) F = Таким образом, схема рис. 7.8,а выполняет операцию “НЕ”. В качестве выходного каскада схемы рис. 7.8,б используется элемент “И-НЕ”, включенный по схеме рис. 7.8,а. Он инвертирует информацию, поступающую с входа первого элемента. Если учесть тождество (7.9), то F = Следовательно, схема рис. 7.8,б выполняет операцию “И”. Информация, поступающая на каждый входной элемент схемы рис. 7.8,в, инвертируется, т.е. F = К основным показателям логических элементов, в первую очередь, относят быстродействие, потребляемую мощность и помехоустойчивость. Быстродействие характеризуется временем задержки реакции выходного сигнала при изменении сигнала на входе элемента. Время задержки логических элементов обычно составляет 0,01 – 0,3 мкс. Их потребляемая мощность обычно находится в пределах от 1 мкВт до 250 мВт и связана с быстродействием: потребляющие большую мощность элементы имеют более высокое быстродействие. При работе логических элементов в составе аппаратуры возможны случаи ложного срабатывания под действием напряжений помех, попадающих на вход микросхемы. Мерой невосприимчивости элементов к помехам является помехоустойчивость, которая зависит от структуры микросхемы, режима работы в ней транзисторов, величины питающего напряжения. Логические функции являются неотъемлемыми компонентами многих формул. Они используются всякий раз, когда необходимо выполнить те или иные действия в зависимости от выполнения каких-либо условий. В Ms Excel имеются следующие логические функции: И, ИЛИ, НЕ, ЕСЛИ Функция И(логическое_значение1; логическое_значение2; ...) – возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ. Пример: =И(2+2=4; 2+3=5) равняется ИСТИНА; если ячейка B4 содержит число между 1 и 100, то: =И(1<B4; B4<100) равняется ИСТИНА Функция ИЛИ(логическое_значение1; логическое_значение2; ...) – возвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ. Функция НЕ(логическое_значение) – меняет на противоположное логическое значение своего аргумента. Функция НЕ используется в тех случаях, когда необходимо быть уверенным в том, что значение не равно некоторой конкретной величине. Пример:=НЕ(1+1=2) равняется ЛОЖЬ. Функция ЕСЛИ(лог_выражение; значение_если_истина; значение_если_ложь) – возвращает значение_если_истина, если заданное условие при вычислении дает значение ИСТИНА, и значение_если_ложь в противном случае. Лог_выражение – это любое значение или выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ. Пример: Предположим, что необходимо записать формулу для вычисления функции F(x)=1-3/х. Значение аргумента содержится в ячейке В2. Функция не определена при х=0. Таким образом, формула примет вид =ЕСЛИ(В2=0;1-3/В2;«Не определено») При конструировании более сложных проверок в качестве значений аргументов значение_если_истина и значение_если_ложь могут быть вложенными до семи функций ЕСЛИ. Пример: Стаж больше или равен 15, то коэффициент равен 1; 10 £ стаж < 15 то коэффициент равен 0,75; 5 £ стаж < 10 то коэффициент равен 0,6; стаж < 5 то коэффициент равен 0,3. Эти условия можно записать с помощью функции ЕСЛИ, при условии, что стаж – это ячейка D2: ЕСЛИ(D2>=15;1;ЕСЛИ(D2>=10;0,75;ЕСЛИ(D2>=5;0,6;0,3)))
29. Сумматор (двоичный одно- и многоразрядный). Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры. Сумматоры классифицируют по различным признакам. В зависимости от системы счисления различают:
По количеству одновременно обрабатываемых разрядов складываемых чисел:
По числу входов и выходов одноразрядных двоичных сумматоров:
По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:
Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединённых цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда.Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени — основная задача при построении параллельных сумматоров. Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных ёмкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса. По способу организации межразрядных переносов параллельные сумматоры, реализующие структурные методы, делят на сумматоры:
Три первых структуры будут подробно рассмотрены в последующих статьях. Среди сумматоров со специальной организацией цепей переноса можно указать:
Сумматоры, которые имеют постоянное время, отводимое для суммирования, независимое от значений слагаемых, называют синхронными. По способу выполнения операции сложения и возможности сохранения результата сложения можно выделить три основных вида сумматоров:
Последние две структуры строятся либо на счётных триггерах (сейчас практически не используются), либо по структуре “комбинационный сумматор – регистр хранения” (сейчас наиболее употребляемая схема). Важнейшими параметрами сумматоров являются:
Одноразрядные сумматоры. Одноразрядные сумматоры предназначены для сложения одноименных разрядов двух слагаемых (хiи уi) с учетом переноса из предыдущего разряда (Рi-1) и вырабатывают в том же машинном такте значения суммы (Si) и переноса в следующий разряд (Pi). Другими словами одноразрядный сумматор складывает три бита xi, yiи Рi-1и формирует Siи Рi. Сумматоры, в которых при сложении двух слагаемых (х и у) не учитывается перенос из младшего разряда, называют полусумматорами. Полусумматор имеет два входа (xiи yi) и два выхода Рiи Si. Таблица истинности полусумматора может быть записана в виде табл. 4.5., по которой записываются логические функции Siи Pi: Табл. 7.1. Табл. 7.2.
Si=xiÅуi=iуi+xi Pi=xiуi
На рис. 7.4. показана схема полусумматора и его обозначение на функциональных схемах. Таблицу истинности одноразрядного сумматора можно записать в виде табл. 4.6. По табл. 7.1составим булевы функции для суммы и переноса: (7.2.) (7.3) Преобразуя (7.1) получим:
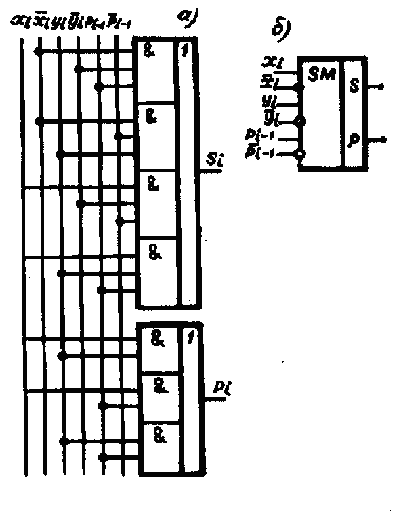
(7.4) Схема одноразрядного сумматора, построенного по формулам (7.2) и (7.3), показана на рис.7.5. Преобразуя формулы (7.2) и (7.3), можно получить различные соотношения, которые позволяют построить различные варианты функциональных схем полного сумматора.
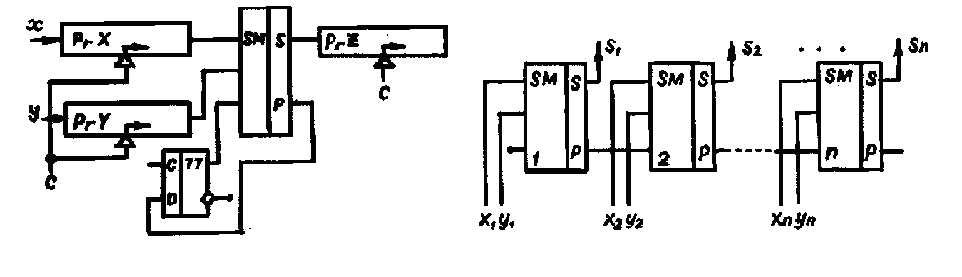
Рис. 7.5. Однорахрядный полный сумматор Многоразрядные сумматоры. В зависимости от того, как обрабатываются (суммируются) разряды n-разрядных чисел, различают многоразрядные сумматоры последовательного и параллельного действия. В последовательных сумматорах поразрядная обработка слагаемых производится последовательно. При этом разряды суммы запоминаются в регистре суммы, а перенос запоминается на один такт в дополнительном триггере. Перенос поступает на вход сумматора вместе со слагаемыми очередного разряда. Процесс продолжается до тех пор, пока полностью не сформируется результат. Структура многоразрядного сумматора последовательного действия показана на рис. 7.6. Сдвигающие регистры РгХ и PrY служат для хранения и сдвига операндов вправо. PrZ - для приема разрядов суммы с выхода одноразрядного сумматора. Поразрядное суммирование производится в сумматоре. Перенос из предыдущего разряда запоминается в D-триггере. В многоразрядных сумматорах параллельного действия разряды слагаемых обрабатываются параллельно. Количество сумматоров в них соответствует разрядности обрабатываемых чисел. По способу реализации цепей переноса сумматоры параллельного действия могут иметь следующую организацию: сумматоры с последовательным, одновременным и групповым переносом. В сумматорах с последовательным переносом перенос распространяется последовательно (рис. 7.7) Максимальное время распространения переноса составляет: tåmax=t1n, где t1- время распространения переноса в одном разряде; n - число разрядов сумматора. В сумматорах параллельного действия с одновременным переносом сигнал переноса вырабатывается одновременно во всех разрядах. Рассмотрим синтез схем одновременного формирования переносов в 4-х разрядных сумматорах.
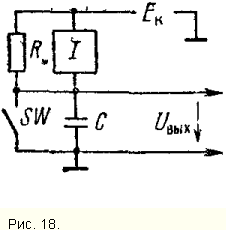
Рис. 7.6. Последовательный сумматор Рис. 7.7.Паралельный сумматор Введем обозначения: hi=xi+уi (7.5) gi=xi·yi(7.6) Подставляя (4.14 и 4.15) в (4.8) для Pi, получим: Pi=gi+hiPi-1(7.7) Функцию gi=xi·yiназывают функцией формирования переноса, а hi=xi+уi- функцией распространения переноса. Путем несложных преобразований из множества аргументов любой функции (4.16) можно исключить все переменные Р1, ...Pn. Например, при n=4 P1=g1+h1P0 P2=g2+h2P1=g2+g1h2+h1h2P0 P3=g3+h3P2=g3+g2h3+g1h2h3+h1h2h3P0 P4=g4+h4P3=g4+g3h4+g2h3h4+h1h2h3h4+h1h2h3h4P0 В этих формулах Р0- внешний перенос. Перенос для i-ro разряда: Pi=gi+gi-1hi+9i-2hi-1hi+...+P0h0h1...hi (7.8) Для образования переносов Р1, P2, ... Рi-1необходимо предварительно получить функции hiи giдля каждого разряда. Функция Siобразуется в соответствии с выражением (4.10) в следующей форме: Si=(xiÅyi)ÅPi-1=(hiÅgi)ÅPi-1=(hi-gi)ÅPi-1=(hi-gi)~Pi-1 (7.9) В таких сумматорах с ростом разрядности возникает потребность в элементах с большим числом входов и большой погрузочной способностью. Например, при n=8 потребуются элементы с числом входов 8 и коэффициентом разветвления 16, что может превышать возможности базовых логических элементов, на основе которых строится сумматор. Поэтому принципы одновременного формирования переносов используются в сумматорах с групповыми переносами. В многоразрядных сумматорах с групповым переносом сумматоры разбиваются по несколько групп (l) по m-разрядов. В таких сумматорах внутри каждой группы используются схемы с одновременным переносом, а между группами - с последовательным или одновременным. Параллельные сумматоры с групповыми переносами, где переносы внутри групп формируются одновременно, а между группами последовательно, называют сумматорами с цепными переносами. В сумматорах с цепными переносами перенос из группы определяется по формуле: Pm=gm-1+hm-1gm-1+...+g0h1h2...hm-1+h0h1...hm-1P0 (7.10) где gi=xi·уi(i=1,2,...,m-1) и Р0- входной перенос. Сумматоры, где переносы внутри групп и между группами формируются параллельно, называются сумматорами с параллельно-параллельным переносом. В таких сумматорах дважды повторяется одна и та же схема для организации одновременного переноса внутри групп и между группами, причем для сумматора в целом группы играют ту же роль, что и одноразрядные сумматоры для групп. Для каждой группы вырабатываются функции генерации (G) и передачи переносов (Н)7. Функция генерации группы G=gm-1+gm-2hm-1+gm-3hm-2hm-1+...+g0h1...hm-1 Функция передачи переносов группы H=h0h1...hm-1 Сигнал переноса для группы вырабатывается согласно формуле Pj=Gj+Gj-1+Gj-2Hj-1+...+G1H1...Hj+PH1...Hj где J=1,l-1 Сумматор с групповой структурой широко применяется в современных ЭВМ. В заключении этого параграфа рассмотрим синтез четырехразрядного двоичногосумматора с одновременным переносом на ПЛМД. Из (4.11) и (4.13) имеем: Si=(xi~уi)Pi-1+(xiÅуi) Pi=(xiyi)+(xi+yi)Pi-1 После несложных преобразований получим:
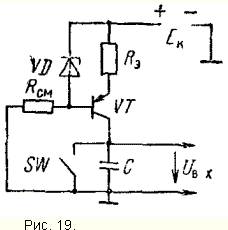
Из множества аргументов любой функции для Sj и Pj можно исключить переменные Р1, P2и Р3. С учетом этого Тогда для
Аналогично для Подсчет показывает, что для реализации четырехразрядного двоичного сумматора с одновременным переносом требуется ПЛМД (5, 5, 25). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 738. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и R
и R  (по цепи положительной обратной связи) и от дополнительного источника U
(по цепи положительной обратной связи) и от дополнительного источника U  .
.
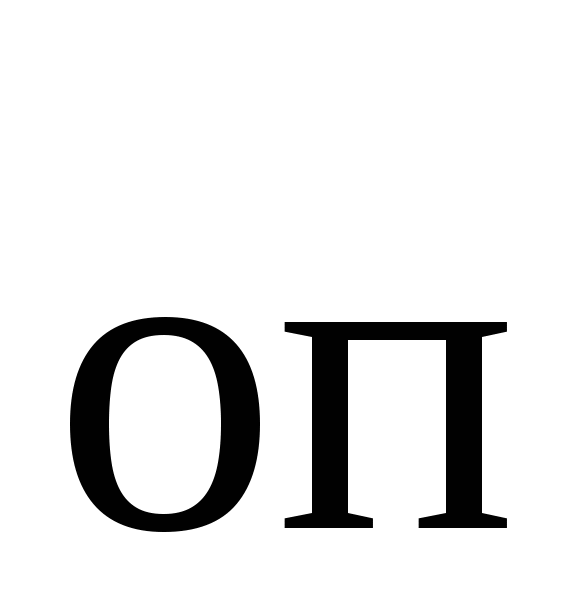 = uвых
= uвых 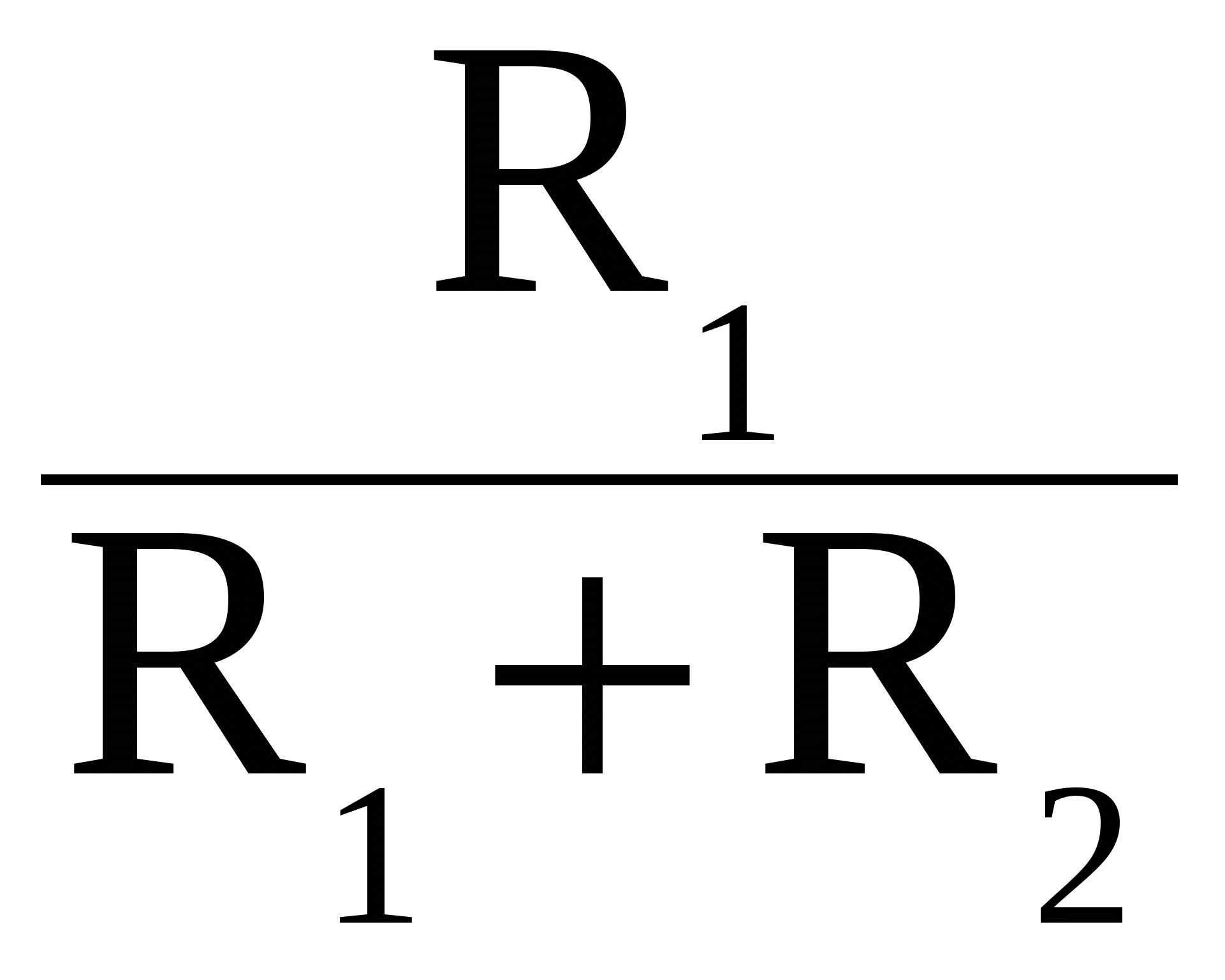 +U
+U 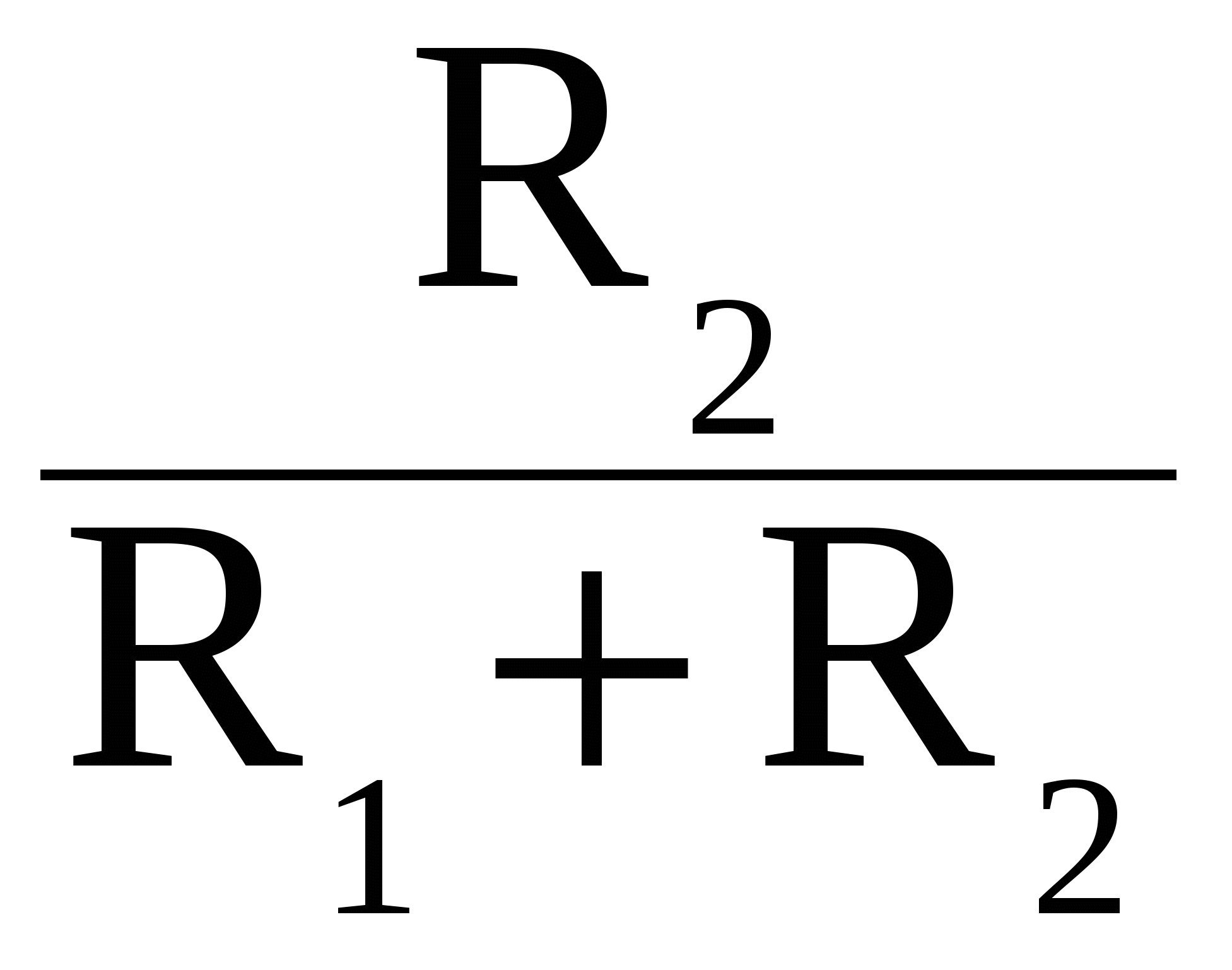 . (5.1)
. (5.1) =U
=U 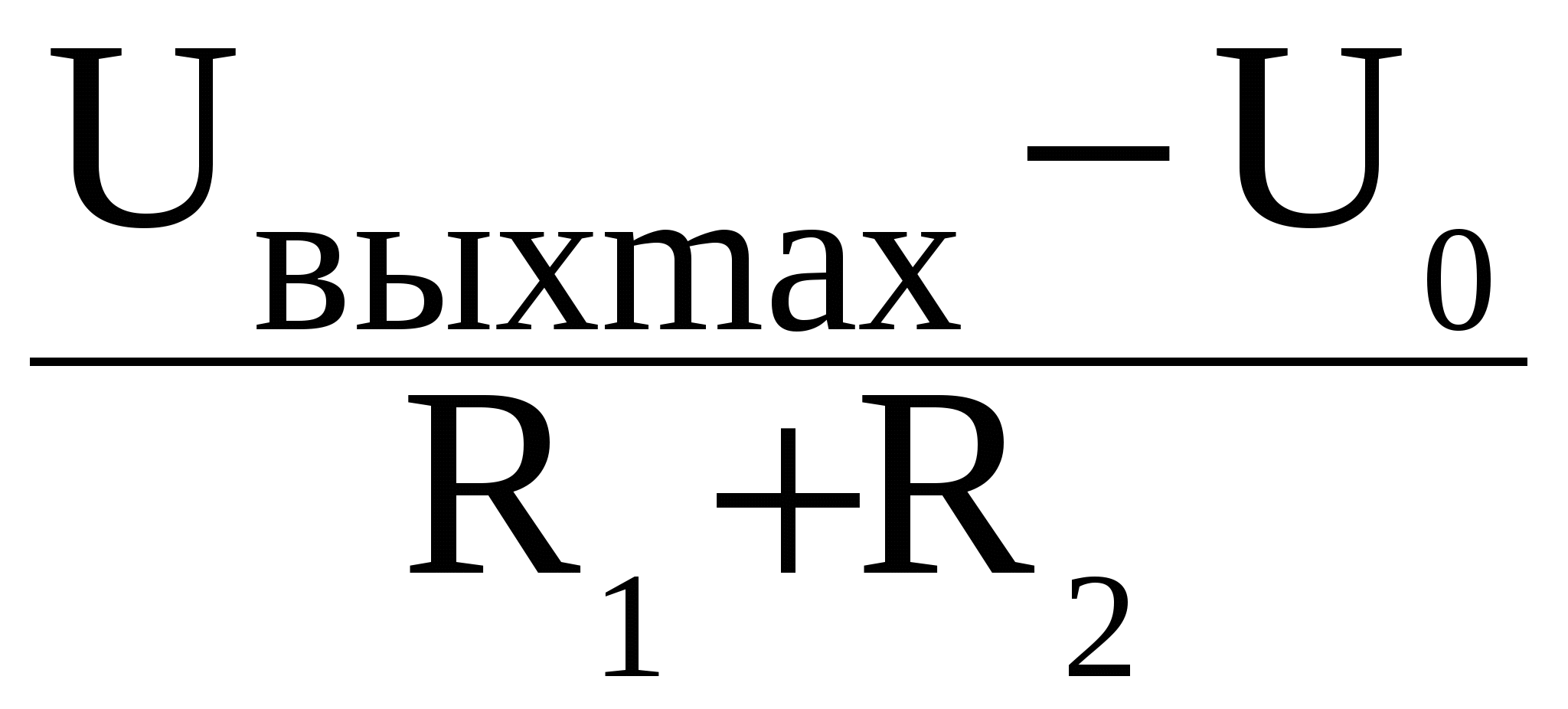 R
R  =U
=U 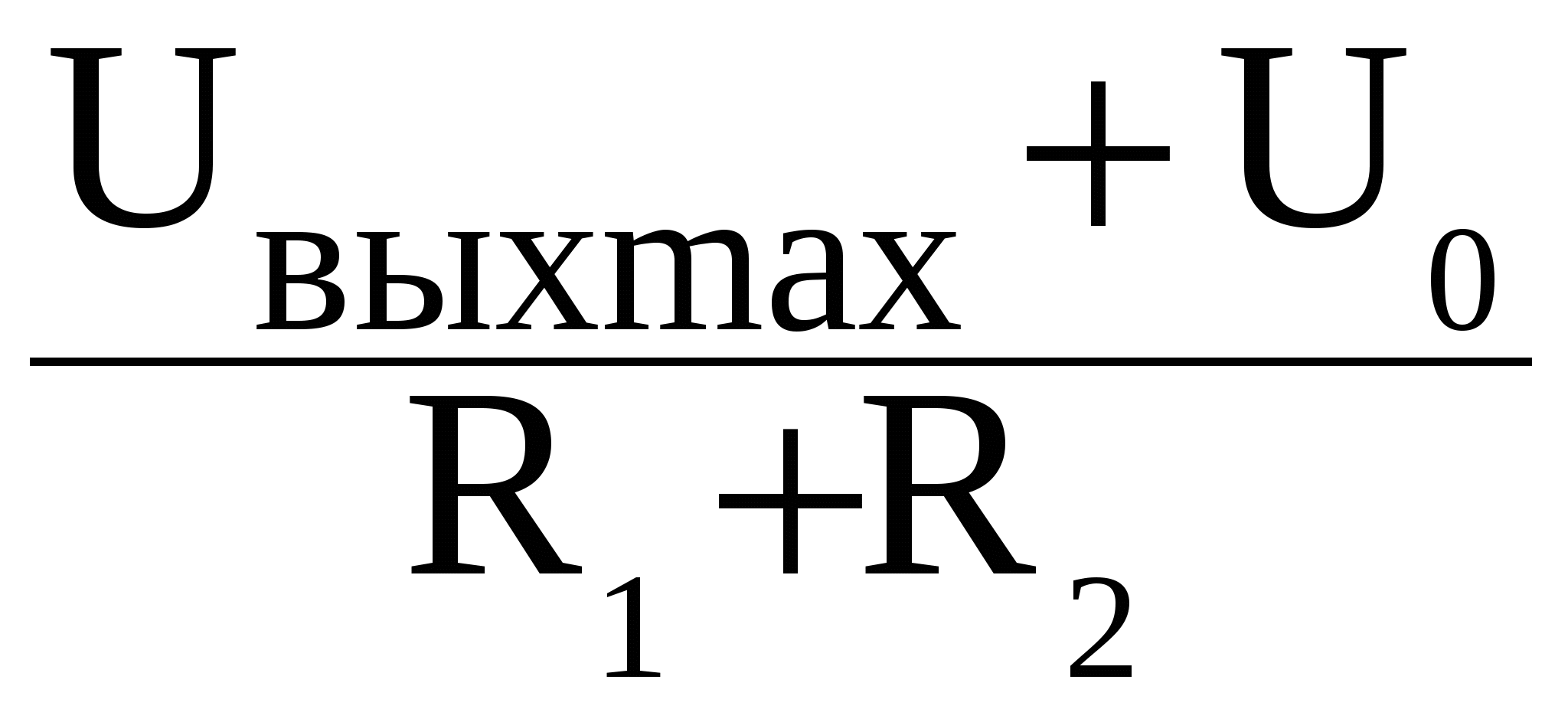 R
R 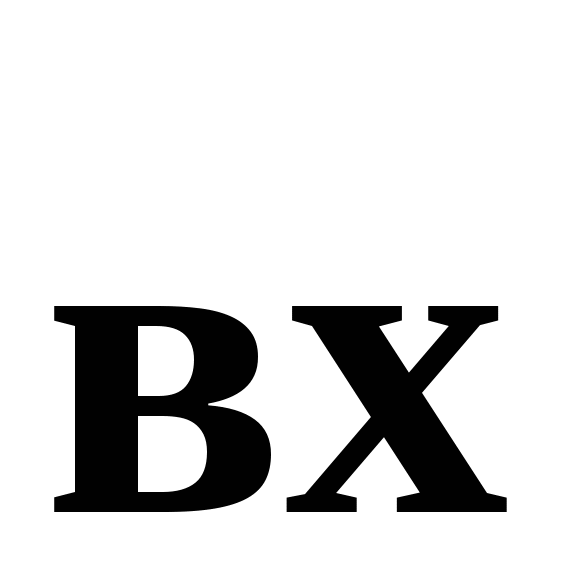 не сравняется с напряжением срабатывания, после чего на выходе ОУ напряжение становится отрицательным и равным -Uвых max. Эта величина выходного напряжения не изменяется при дальнейшем увеличении входного напряжения. При опрокидывании схемы напряжение на неинвертирующем входе также скачком изменится и станет равным напряжению отпускания U
не сравняется с напряжением срабатывания, после чего на выходе ОУ напряжение становится отрицательным и равным -Uвых max. Эта величина выходного напряжения не изменяется при дальнейшем увеличении входного напряжения. При опрокидывании схемы напряжение на неинвертирующем входе также скачком изменится и станет равным напряжению отпускания U 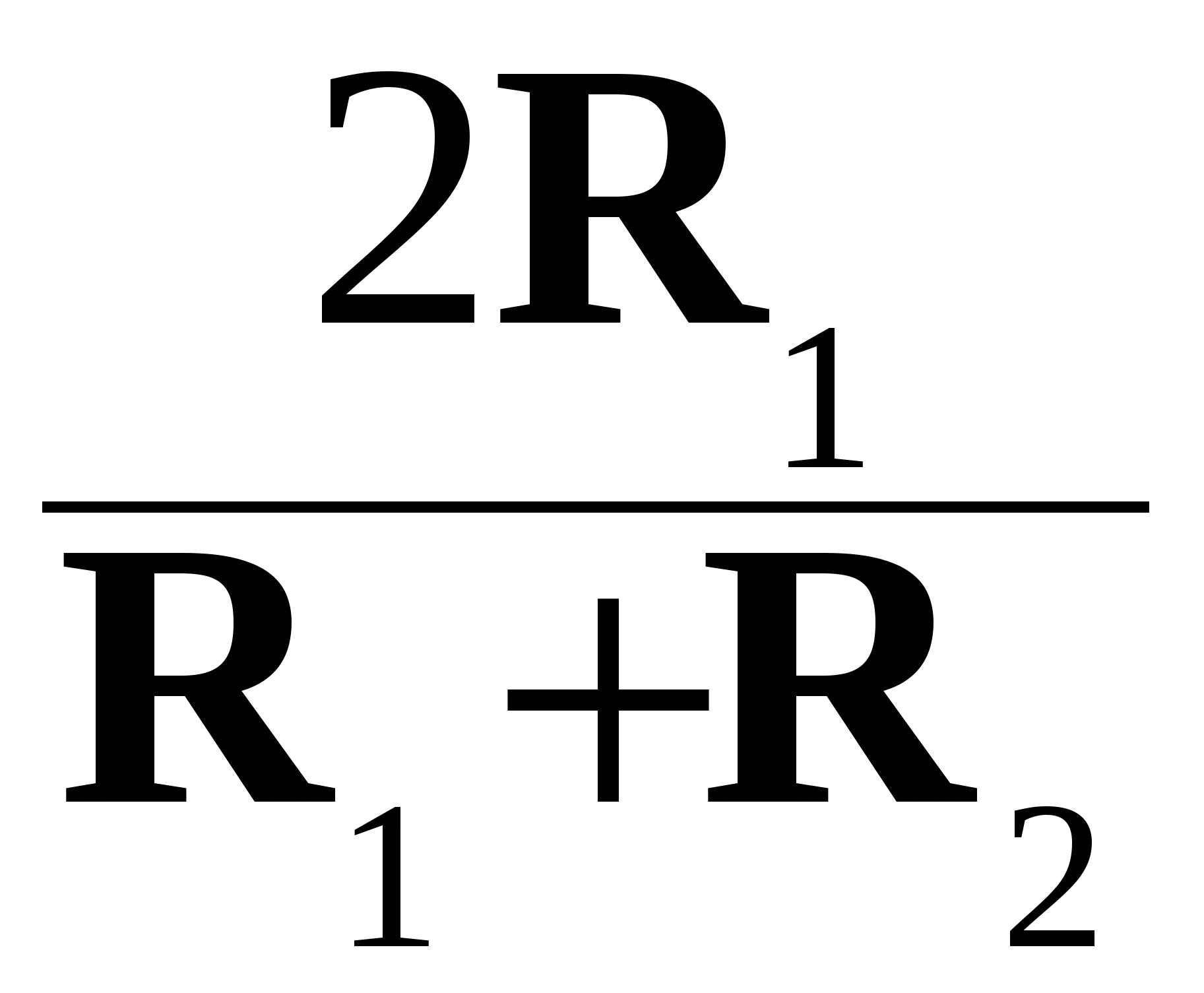 Uвыхmax, (5.4)
Uвыхmax, (5.4)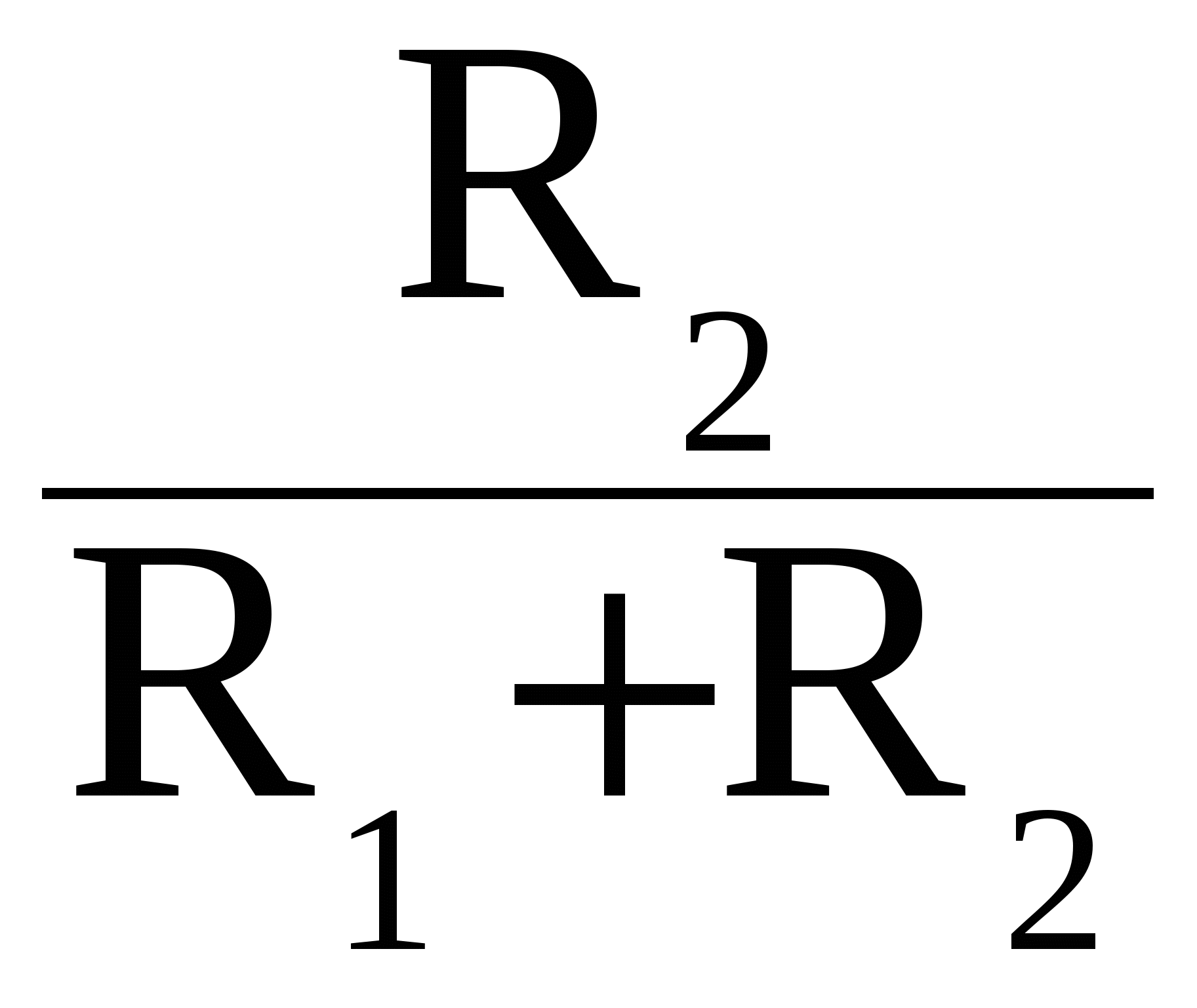 . (5.5)
. (5.5)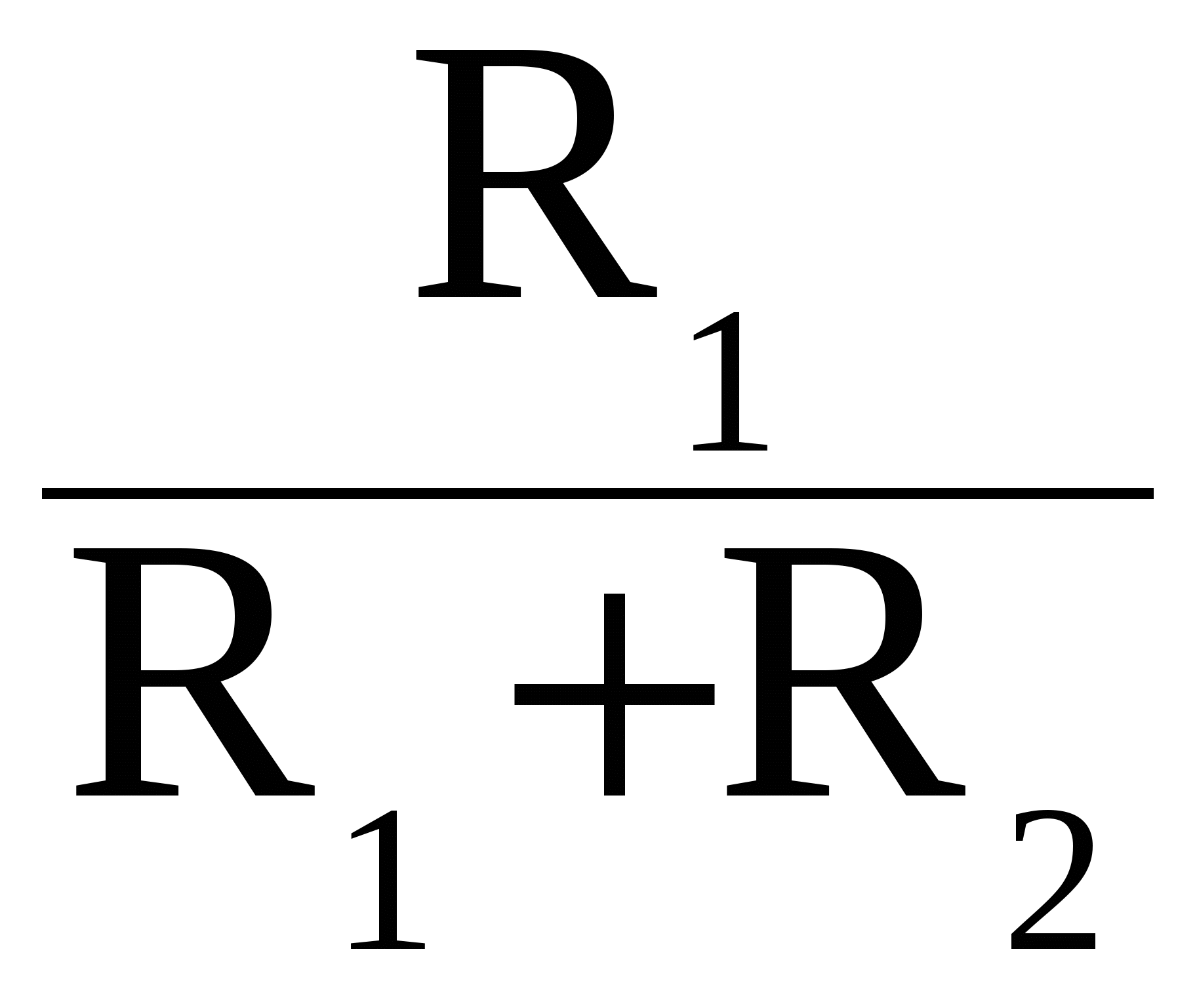 + uвх
+ uвх 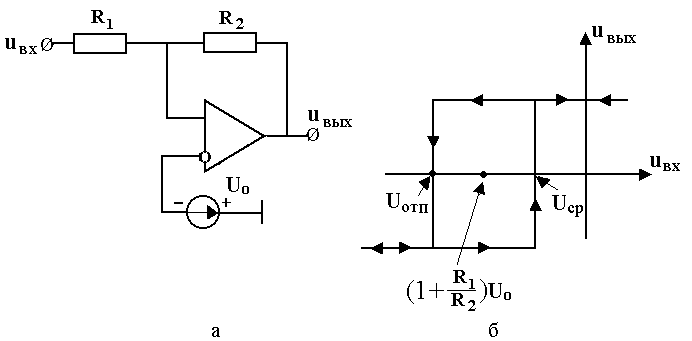
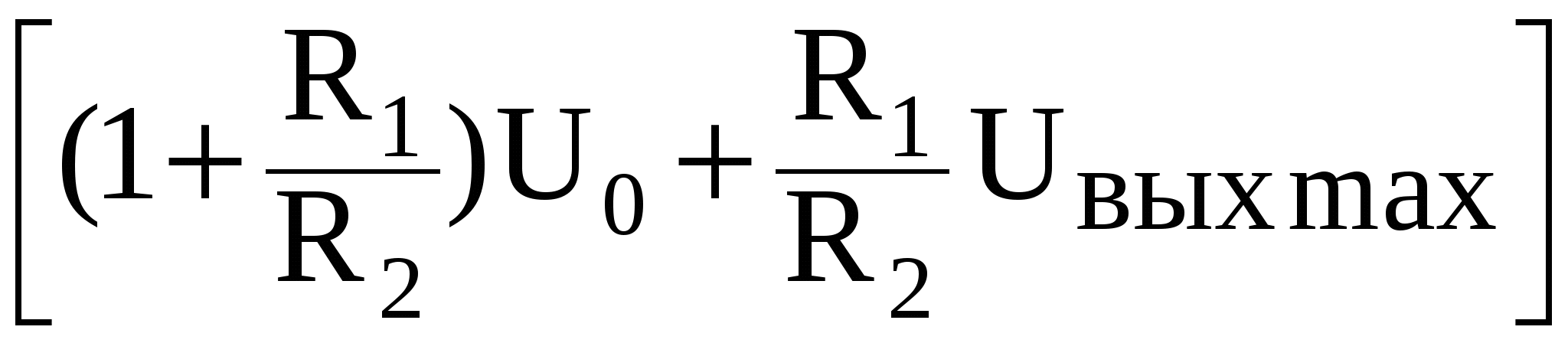 , (5.7)
, (5.7)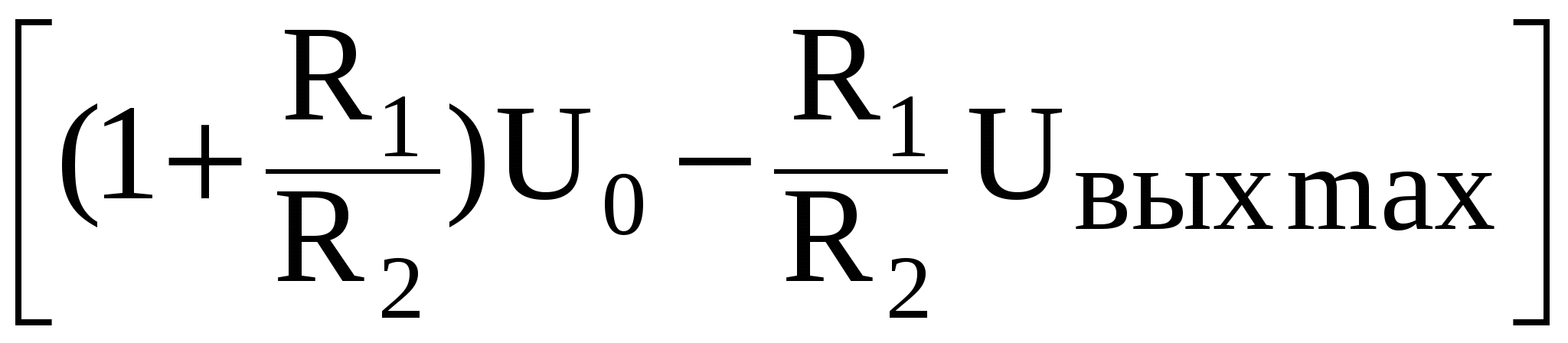 . (5.8)
. (5.8)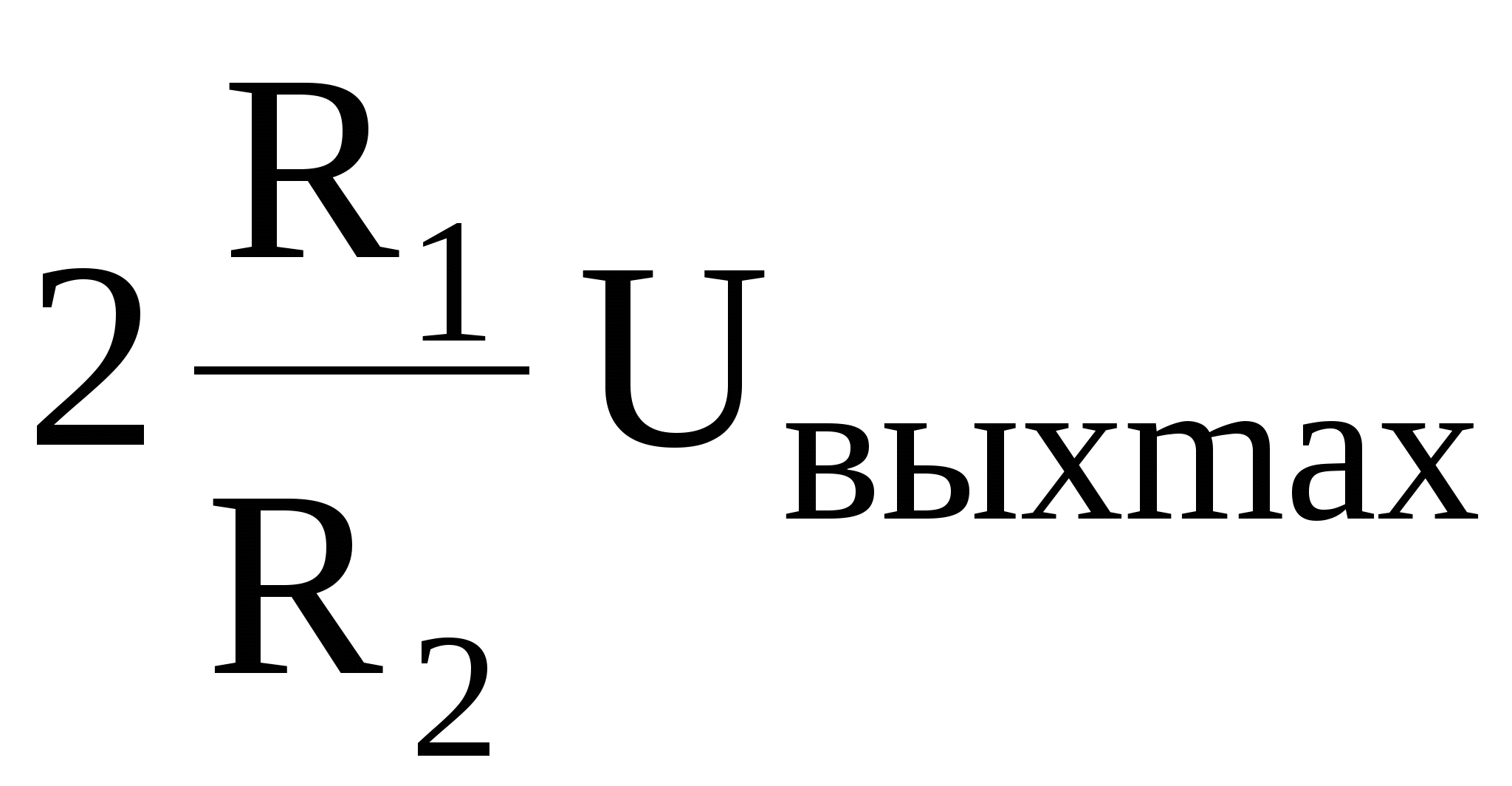 , (5.9)
, (5.9)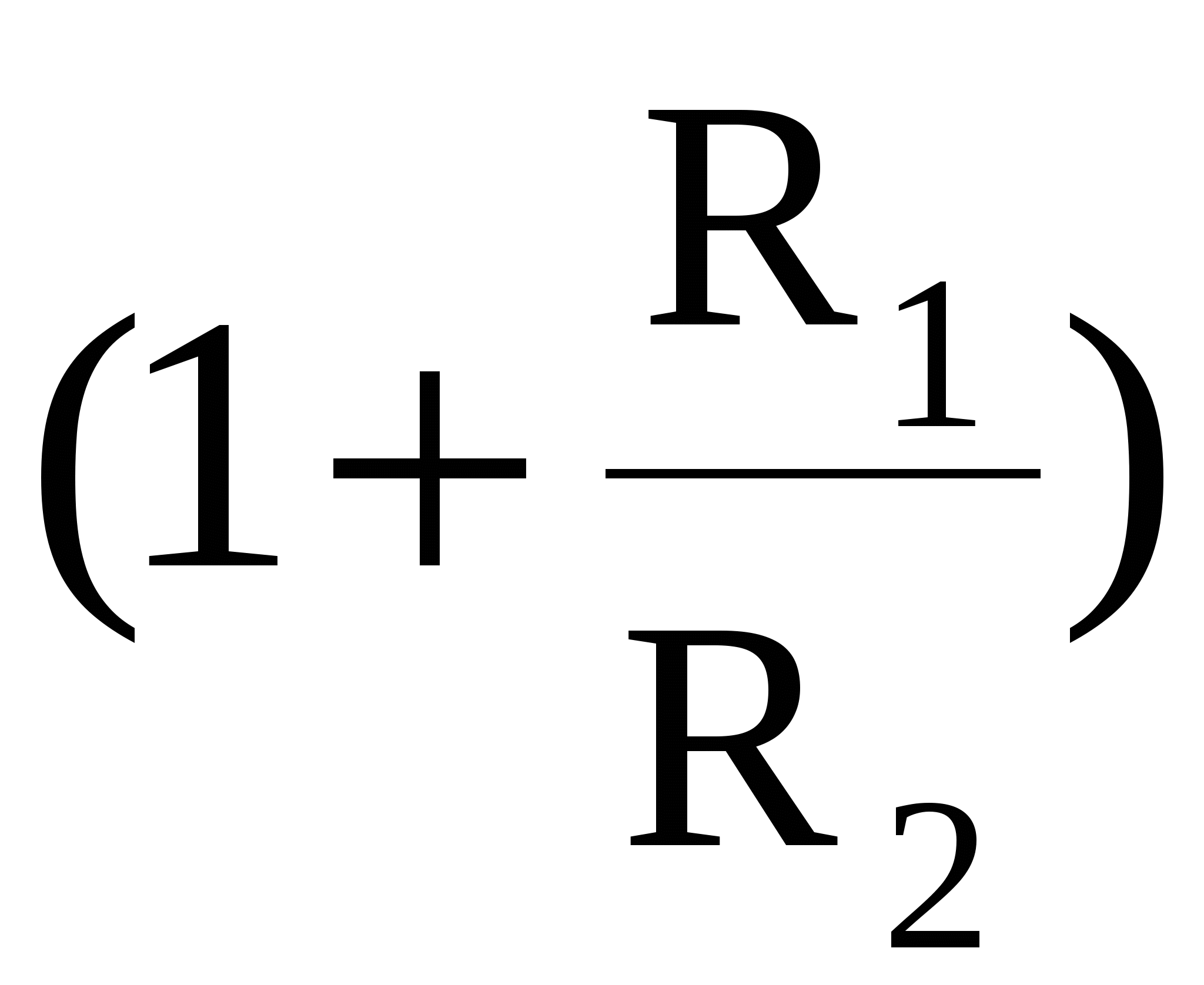 . (5.10)
. (5.10)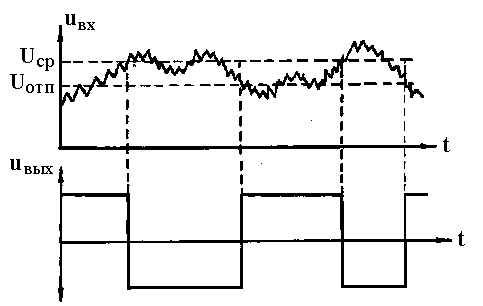
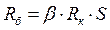
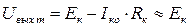
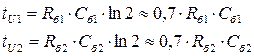
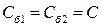 и
и 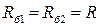 длительность импульса
длительность импульса 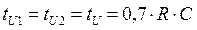 , а периода колебаний
, а периода колебаний 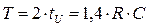 .
.
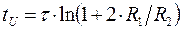
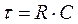
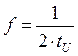
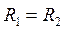 частота генерации
частота генерации 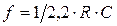 .
.
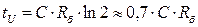
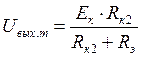
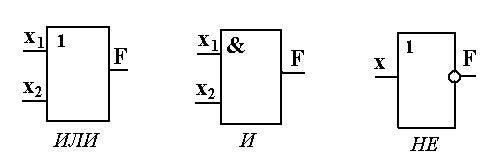
 = 0, гдеi = 1, 2, … n)все диоды будут находиться в закрытом состоянии и на резисторе падение напряжения равно нулю(F = 0).При подаче хотя бы на один вход схемы сигнала положительной полярности диод, установленный на этом входе, перейдет в открытое состояние. Через него и последовательно включенный с ним резисторRбудет протекать ток, падение напряжения на резисторе будет отличаться от нуля.F = 1.
= 0, гдеi = 1, 2, … n)все диоды будут находиться в закрытом состоянии и на резисторе падение напряжения равно нулю(F = 0).При подаче хотя бы на один вход схемы сигнала положительной полярности диод, установленный на этом входе, перейдет в открытое состояние. Через него и последовательно включенный с ним резисторRбудет протекать ток, падение напряжения на резисторе будет отличаться от нуля.F = 1.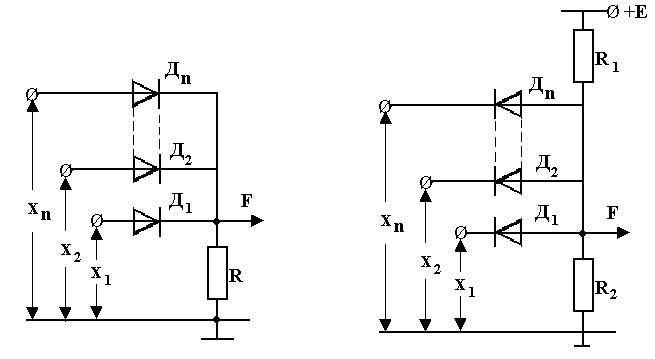
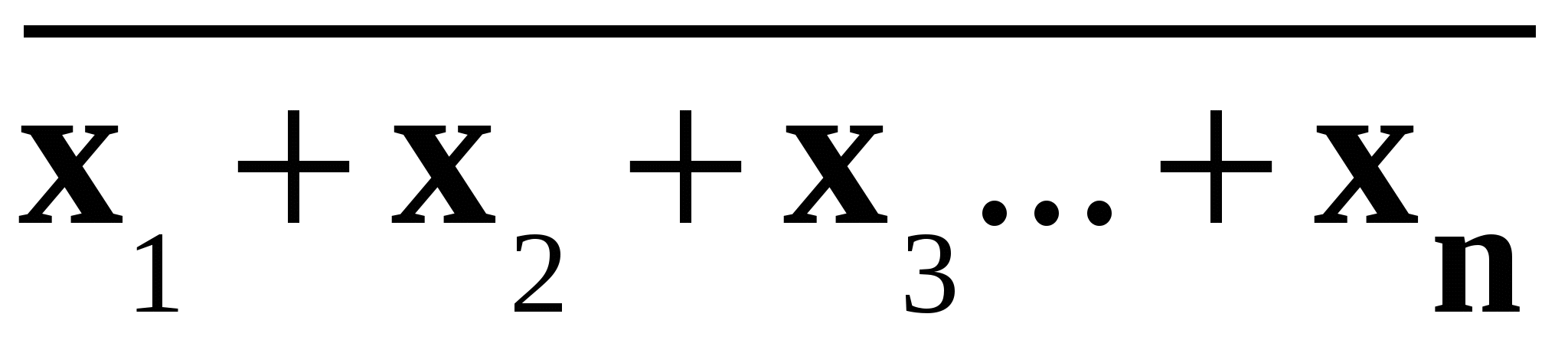 иF =
иF = 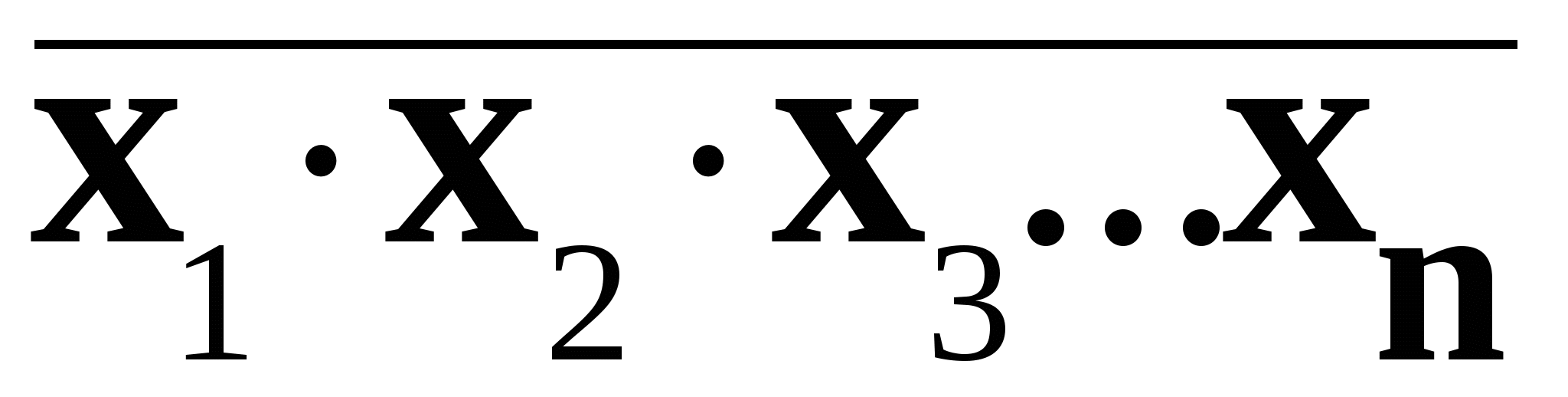 .
.
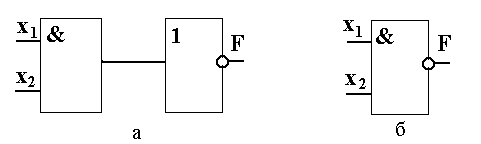
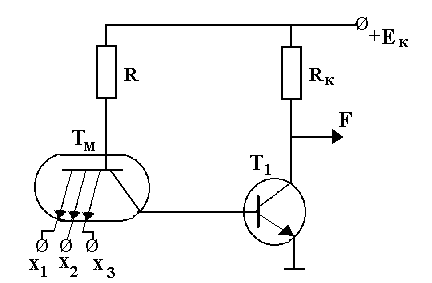
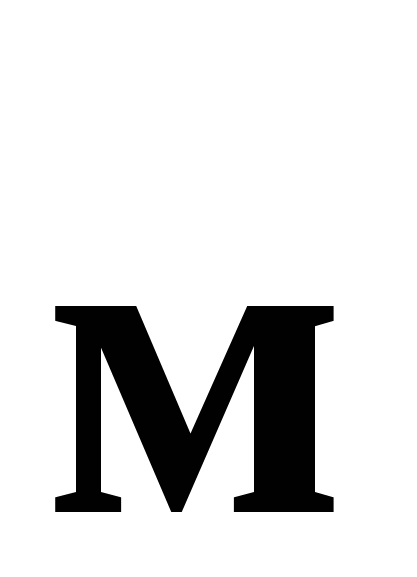 , которым заменяется диодная часть элемента “И-НЕ”, выполняющего операцию “И”. В многоэмиттерном транзисторе эмиттерный слой состоит из нескольких областей при общих базовом и коллекторном слоях. Принцип работы схемы рис. 7.7 следующий. Если на все эмиттерные входы транзистораТ
, которым заменяется диодная часть элемента “И-НЕ”, выполняющего операцию “И”. В многоэмиттерном транзисторе эмиттерный слой состоит из нескольких областей при общих базовом и коллекторном слоях. Принцип работы схемы рис. 7.7 следующий. Если на все эмиттерные входы транзистораТ  (т.е. всеx
(т.е. всеx 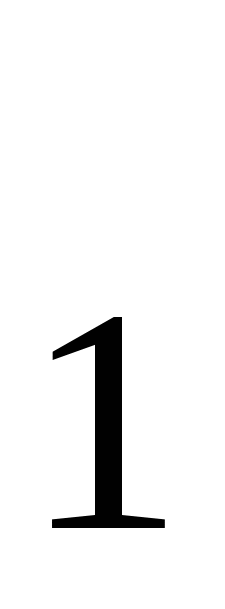 . ТранзисторТ
. ТранзисторТ 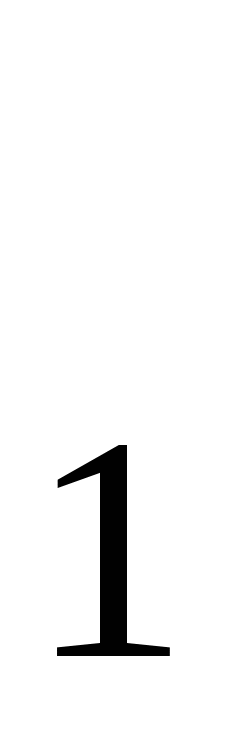 , который выполняет операцию логического отрицания, в этом случае будет находиться в открытом состоянии, и на его выходе напряжение будет практически отсутствовать(F = 0). При отсутствии хотя бы на одном эмиттерном входе транзистораТ
, который выполняет операцию логического отрицания, в этом случае будет находиться в открытом состоянии, и на его выходе напряжение будет практически отсутствовать(F = 0). При отсутствии хотя бы на одном эмиттерном входе транзистораТ 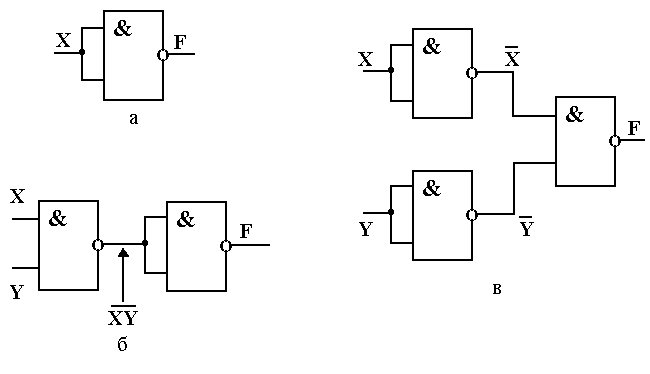
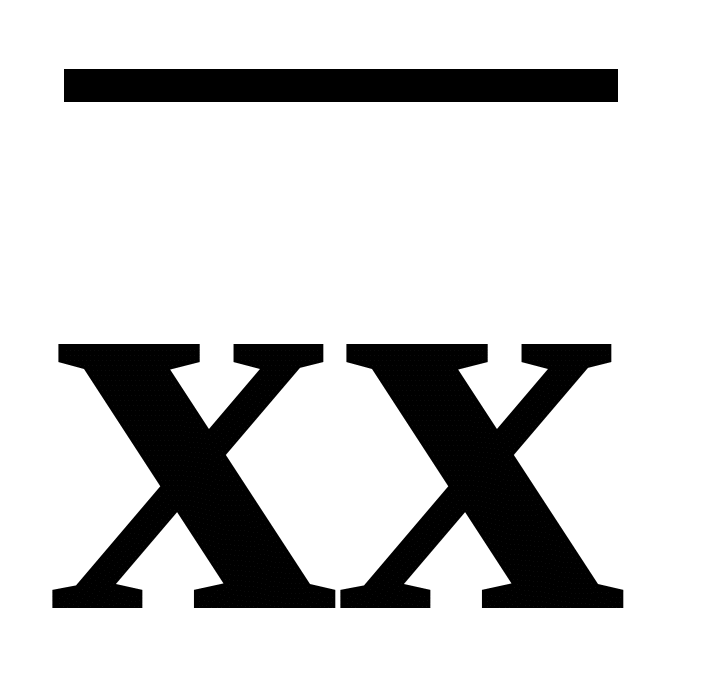 =
=  +
+ 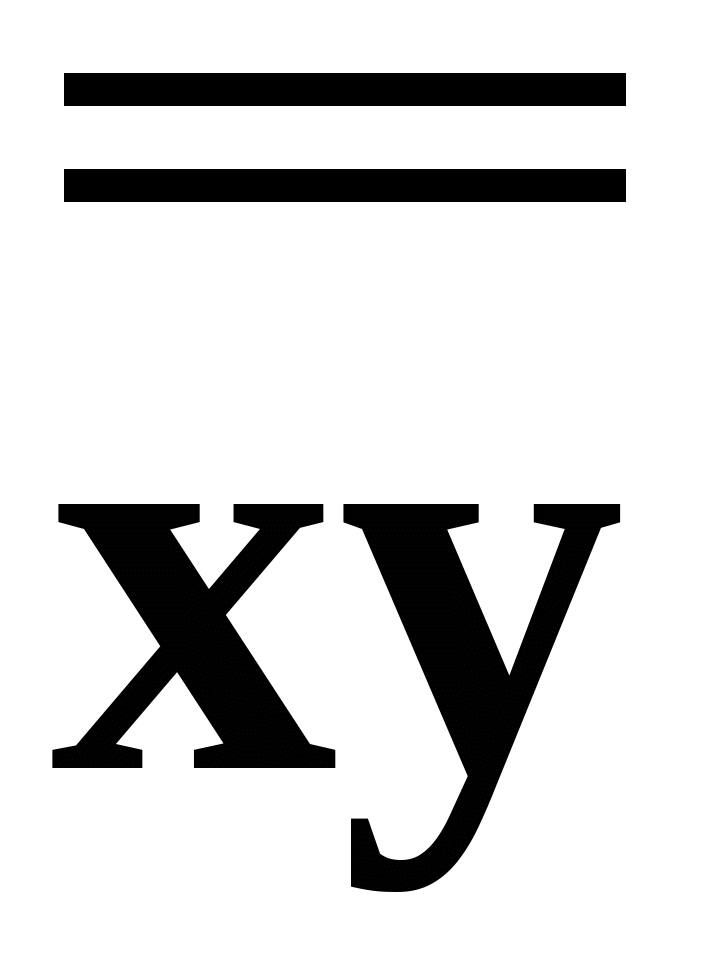 =xy.
=xy. . Тогда последовательное использование тождеств (7.11) и (7.9) позволяет показать, что эта схема реализует операцию логического сложения “ИЛИ”
. Тогда последовательное использование тождеств (7.11) и (7.9) позволяет показать, что эта схема реализует операцию логического сложения “ИЛИ”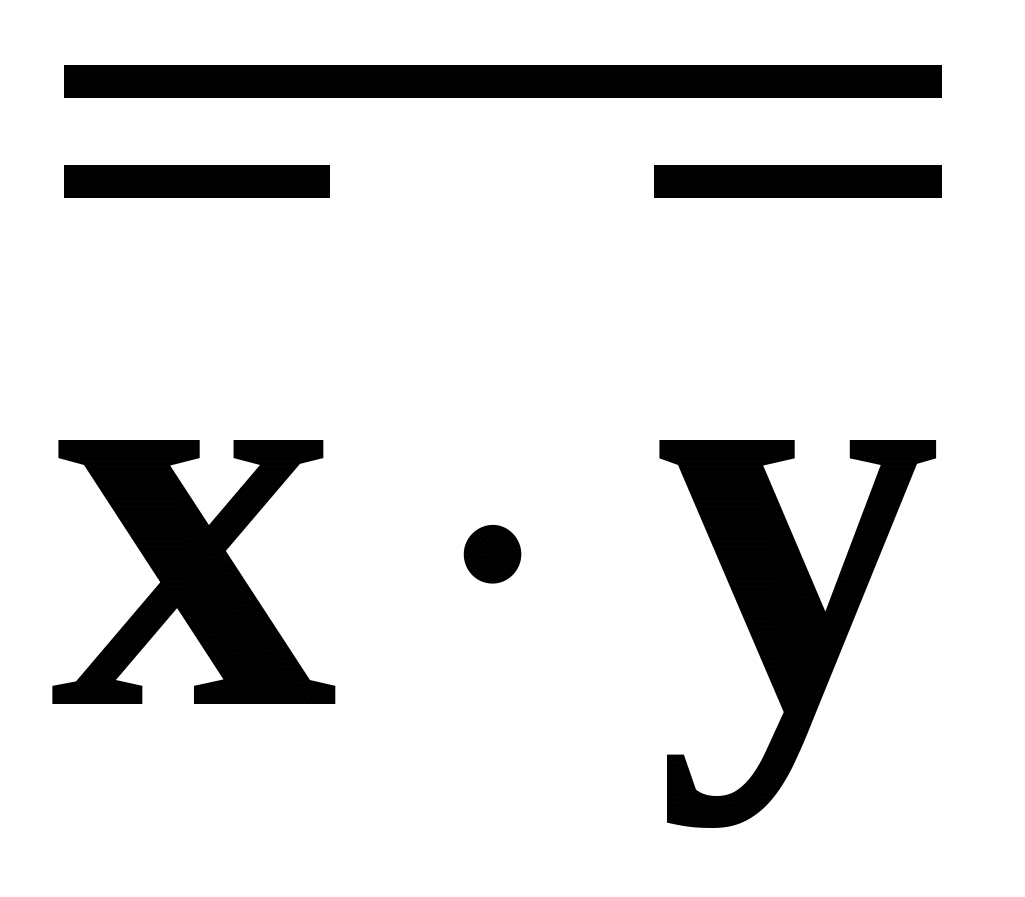
 =
= 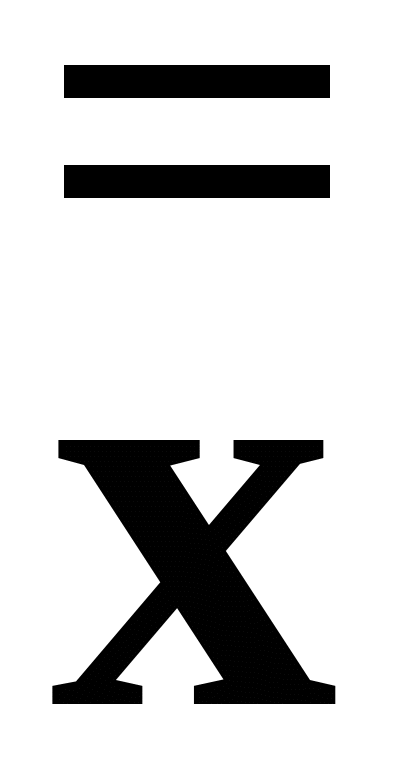 +
+  = x + y.
= x + y.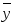 i; (7.1)
i; (7.1)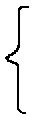
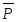 i-1
i-1