
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
КОНТРОЛЬНЫЙ ПРИМЕР ДЛЯ АЛГОРИТМА УТОЧНЕНИЯ КОРНЯ МЕТОДОМ КАСАТЕЛЬНЫХВычислить корень уравнения F(x) = x – sin x – 0,25 = 0 на отрезке [1,1; 1,2] с точностью 10–6. Ответ: х = 1,171229656. Замечание. F¢(x) = 1 – cos x; x0 = b = 1,2. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ 1.Что позволяет найти объединенный алгоритм? 2.Каким способом уточняются значения изолированных корней в объединенном алгоритме? Каковы способы уточнения корней? 3. Как узнать, сменила ли функция знак? 4. Что является признаком окончания цикла в методе половинного деления? 5. На чем основан метод касательных? 6.Как определяют точку начального приближения в методе касательных? 8.Что является признаком окончания вычислительного процесса в методе касательных? Для закрепления изученного материала следует выполнить лабораторную работу №5.
ЛАБОРАТОРНАЯ РАБОТА № 5 Уточнение корней уравнений объединенным методом и методом касательных Задание к лабораторной работе. Заданы два уравнения (см. условие лабораторной работы №4). Для первого уравнения по программе, реализующей объединенный алгоритм, отделить его корни, а затем найти их значения с точностью 0,001. Для второго уравнения аналитически отделить корни, а затем по программе, реализующей метод касательных, найти их значения с точностью 0,001. ЛЕКЦИЯ 5 УТОЧНЕНИЕ ЗНАЧЕНИЯ ИЗОЛИРОВАННОГО КОРНЯ УРАВНЕНИЯ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ В переводе с латыни iteratio означает “повторение”. Метод простых итераций (МПИ) основан на представлении уравнения F(x) = 0 (5) в виде х = f (x). (6). Уравнение (6) равносильно уравнению (5).  Пусть x - корень уравнения (6), а х0 - полученное каким-то способом грубое приближение к корню. Подставим х0 в правую часть (6), получим некоторое число х1 = f (x0). Сделаем то же самое с х1, получим х2 = f(x1) и т. д. Последовательно применяя соотношение хn = f (xn–1) для n = 1,2, ..., получим числовую последовательность х0, х1, ... , хn, ... (7) Она называется последовательностью приближений или итерационной последовательностью. Справедливо утверждение: если последовательность (7) сходится, а функция f(x) непрерывна, то предел последовательности (7) является корнем уравнения (6). Действительно, пусть x = Метод итераций не всегда приводит к уточнению корня. Достаточные условия сходимости итерационного процесса выясняются следующей теоремой (дез доказательства). Теорема. Пусть уравнение х = f (x) имеет единственный корень на отрезке [а, b], и выполняются следующие условия: 1) f(x) определена и дифференцируема на отрезке [a, b]; 2) f (x) Î [а, b] для всех х Î[а, b]; 3) существует такая правильная дробь q, что для всех х из отрезка [а, b] ½f '(x)½ £ q < 1. Тогда итерационная последовательность хn = f (xn–1) (n = 1,2, ...) сходится при любом начальном х0 Î[а, b]. Эта теорема лежит в основе метода простых итераций. Уравнение F(x) = 0 может быть приведено к виду х = f (x) многими способами, главное, чтобы выполнялись условия (1-3) сформулированной теоремы. Уточним значение корня методом итераций на конкретном примере. Пусть уравнение вида (5) следующее: lg (2x + 3) = 1 - 2x. Для нахождения интервала, содержащего корень, применим графический метод. Построим графики функций у1 = lg (2x + 3) и у2 = 1 − 2x. Абсцисса точки пересечения графиков и определит интервал изоляции корня данного уравнения.
Рис.13. Иллюстрация к графическому методу отделения корней
Из графика на рис.13 видно, что корень уравнения (5) содержится в интервале [0; 0,5], т.к. прямая у2 = 1−2x пересекает ось Х в точке (0,5; 0). Уточним значение корня, находящегося в этом интервале с точностью e = 0, 0001. Для уточнения его значения приведем уравнение (5) к виду х = f (x) (6). Для этого оставим слева от знака равенства х, а все остальные члены перенесем вправо от знака равенства, произведя необходимые действия. Получим выражение 2х = 1 - lg (2x + 3), х= Легко показать, что условия теоремы о сходимости итерационного процесса для уравнения (8) выполняются. Следовательно, мы можем для поиска приближенного значения корня применить метод простых итераций. За начальное приближение к корню возьмем левый конец отрезка, содержащего корень, т.е. х0 = 0. Все остальные приближения будем находить по рекуррентной формуле хn+1 = Вычисления следует продолжать до тех пор, пока ½F(x) - x½> e . Результаты промежуточных вычислений представим в таблице 5.1. Таблица 5.1 — Результаты промежуточных вычислений для метода простых итераций
Уточненное значение корня х = 0,2304.
АЛГОРИТМ МЕТОДА ПРОСТЫХ ИТЕРАЦИЙ
ШАГ 1. Вводим исходные данные для нахождения корня, а именно, значения а - левый конец отрезка, содержащего корень, b - правый конец отрезка, e - требуемая точность вычислений. ШАГ 2. Определяем либо подпрограмму, либо функцию для вычисления правой части уравнения (6). ШАГ 3. Организуем счетчик итераций n и полагаем его равным нулю, n=0. ШАГ 4. Берем в качестве начального приближения к корню левый конец отрезка, содержащего корень, т.е. х = а. ШАГ 5. Вычисляем значение функции в точке начального приближения, т.е. у = F(x). ШАГ 6. Сравниваем абсолютную величину разности между у и х с e: если ½у – x½ < e , то переходим на шаг 10. ШАГ 7. Печатаем текущее значение счетчика итераций, приближения к корню и значение функции в этой точке, т.е. n, x, F(x). ШАГ 8. Увеличиваем счетчик итераций на единицу, т.е. n = n + 1. ШАГ 9. Запоминаем текущее значение функции в качестве очередного приближения, т.е. х = F(x). Переходим на шаг 5. ШАГ 10. Выводим на печать найденное значение корня х. ШАГ 11. Конец задачи. В качестве контрольного примера к методу итераций следует взять пример, рассмотренный в данной лекции. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ 1. Каким образом должно быть представлено уравнение, для которого требуется найти корень методом простых итераций? 2. Cформулируйте достаточные условия сходимости итерационного процесса для метода простых итераций. 3. Сформулируйте пошаговый алгоритм нахождения изолированного корня трансцендентного уравнения методом простых итераций. 4. Что является признаком окончания вычислительного процесса в методе простых итераций? |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 219. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
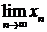 . Перейдем к пределу в равенстве хn = f(xn–1). Тогда
. Перейдем к пределу в равенстве хn = f(xn–1). Тогда  =
= 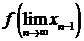 = f(x), т.е. x = f (x).
= f(x), т.е. x = f (x).
 . (8)
. (8) . (9)
. (9)