КОНТРОЛЬНЫЙ ПРИМЕР К АЛГОРИТМУ ОТДЕЛЕНИЯ КОРНЕЙ

ЧИСЛЕННЫЕ МЕТОДЫ

Учебное пособие

Для бакалавров

Строительного института

Екатеринбург 2017

УДК 519.47(075.84)

ББК 143я73

М64

Рецензент:

Доктор физико-математических наук, профессор

В.Н. Сыромятников

    Миронова Л.И.

М64 Численные методы: учебное пособие // конспект лекций и практических заданий / Людмила Ивановна Миронова; Урал. федер. ун-т. – Екатеринбург, 2017, 127 с.

ISBN ________________

В пособии содержится теоретический и практический материал по численным методам. Рассмотрены основные методы приближенных вычислений. Изложение каждого метода заканчивается описанием алгоритма для реализации метода на компьютере.

Теоретический материал изложен в виде лекций, после каждой из которых приведены вопросы для самопроверки. Для каждой теоретической темы разработано практическое задание с вариантами индивидуальных заданий. Выполнение практического задания требует начальных навыков в области работы с MS  Excel.

Пособие предназначено для бакалавров, обучающихся по направлению подготовки «010500.62 – Строительство».

УДК 519.47(075.84)

ББК 143я73

ISBN ________________                             ©Уральский федеральный                              университет, 2017

© Миронова Л.И., 2017

ВВЕДЕНИЕ

    Процесс решения задачи с помощью компьютера включает в себя следующие этапы:

    1. Постановка задачи и построение математической модели.

    2. Разработка алгоритма решения задачи.

    3. Запись алгоритма на языке программирования.

    4. Исполнение программы на компьютере.

    5. Анализ полученных результатов.

    Наиболее сложным и ответственным этапом в этом процессе является этап 1 - построение математической модели, т.е. описание наиболее существенных свойств реального объекта и их взаимосвязь с помощью математических соотношений (это может быть уравнение, система линейных уравнений, система дифференциальных уравнений и т.п.).

    Если выбранная модель груба, то какие бы изощренные методы решения вслед за этим не применялись, результат вряд ли будет удовлетворительным. Этот шаг дает так называемую погрешность модели.

    Определенные трудности вызывает и этап 2 - разработка алгоритма, когда подыскивается метод решения задачи в рамках созданной математической модели. Здесь возникает так называемая погрешность метода.

    Часто оказывается, что даже для достаточно простых моделей не удается получить результат в аналитическом виде (т.е. в виде формулы). В таких случаях весь арсенал методов “точной” математики оказывается беспомощен.

Тогда используют приближенные математические методы, которые позволяют получить вполне удовлетворительные результаты.

    Основными приближенными методами являются численные методы, при использовании которых результат получается путем многократных вычислений. Очевидно, что наиболее естественный путь реализации численных методов – это использование компьютера.

    Использование компьютера влечет за собой (из-за резкого возрастания количества выполняемых операций) увеличение погрешности результата. Появляется так называемая вычислительная погрешность.

    Отметим факторы, влияющие на общую погрешность результата, более подробно.

    Пусть R - точное значение результата решения некоторой задачи. Из-за несоответствия математической модели реальному объекту, а также по причине неточности исходных данных вместо R был получен результат R₁. Возникает абсолютная погрешность. Ее называют неустранимой погрешностью.

    Далее, в рамках разработанной модели мы выбираем некоторый численный метод (еще не приступив к вычислениям) и получаем вместо R₁ результат R₂. Тогда абсолютная погрешность  называется погрешностью метода.

    Наконец, в результате ограничений разрядной сетки машины и неизбежных многократных округлений накапливается погрешность, приводящая к результату R₃ вместо R₂. Абсолютная погрешность  называется вычислительной погрешностью.

        Тогда значение полной абсолютной погрешности . Преобразуем это выражение. Для этого добавим и вычтем из его правой части R₁ и R₂, а затем перегруппируем слагаемые:

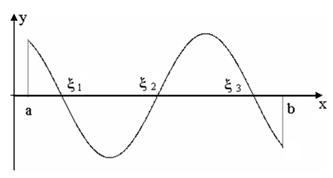
Полная абсолютная погрешность ε не превосходит суммы абсолютной неустранимой погрешности, абсолютной погрешности метода и абсолютной погрешности вычислений.

    Поскольку абсолютные погрешности e₁, e₂ и e₃ в большинстве случаев остаются неизвестными (ибо неизвестно истинное значение результатов R, R₁ и R₂), то на практике удается получить лишь их абсолютные верхние оценки D₁, D₂ и D₃ и приходится довольствоваться лишь оценочными представлениями общей погрешности: e £ D₁+D₂+D₃ ,

где D₁ ³½R₁ - R½, D₂ ³ ½R₂ - R₁½и D₃ ³ ½R₃ - R₂½.

Ниже мы рассмотрим наиболее распространенные численные методы вместе с алгоритмами, их реализующими. По каждому численному методу представлены варианты лабораторной работы, в которой по рассмотренному алгоритму следует составить программу на любом известном студенту языке программирования, решить по ней контрольный пример, рассмотренный в лекции, а затем выполнить индивидуальное задание.

Лекция 1

 РЕШЕНИЕ УРАВНЕНИЙ С ОДНИМ НЕИЗВЕСТНЫМ

        Рассмотрим четыре численных метода решения уравнений с одним неизвестным, а именно:

    1) метод половинного деления,

    2) метод хорд,

    3) метод касательных,

    4) метод простых итераций.

    Пусть дано уравнение

F(х) = 0.                                                (1)

Чтобы решить уравнение (1), надо ответить на следующие вопросы:

    1) Имеет ли оно корни?

    2) Если имеет, то сколько их?

    3) Каковы значения всех корней с заданной точностью?

    Поскольку подавляющее большинство уравнений вида (1) не решается точными методами (путем аналитических преобразований), будем рассматривать названные численные методы.

    Прежде чем приступить к применению этих методов решения уравнения (1), отметим следующий момент. К каждому из этих методов относится этап отделения корней, т.е. установления некоторых промежутков в области определения функции F(х), содержащих по одному корню. Мы рассмотрим два метода «ручного» отделения корней: графический и аналитический.

    Но прежде дадим несколько определений и приведем формулировки теорем (без доказательства), чтобы теоретически обосновать дальнейшие рассуждения.

    Определение 1.Функция у = f(х) называется непрерывной в точке х₀, если при стремлении абсциссы х к значению х₀ордината у = f(х) графика функции стремится к значению f(х₀).

    Иначе свойство непрерывности функции можно выразить так: функция является непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

    Определение 2. Функция называется непрерывной на данном промежутке,если она непрерывна в каждой точке этого промежутка.

    Теорема 1.Если функция f(х) непрерывна на отрезке [a, b] и принимает на концах отрезка значения разных знаков, то внутри этого отрезка существует, по меньшей мере, один корень уравнения (1).

    Иллюстрацией к этой теореме служат рис.1 и рис.2.

Рис.1. Иллюстрация к теореме 1, когда на отрезке [a, b] существуют несколько корней

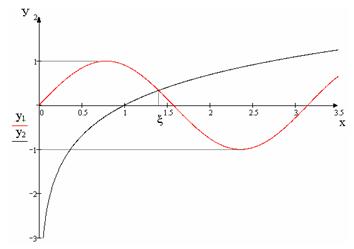
Рис.2. Иллюстрация к теореме 1, когда на отрезке [a, b] существует единственный корень

    Важно уметь отделять промежутки, содержащие по одному корню. Этот вопрос позволяет решить следующая теорема 2. Но сначала дадим несколько определений.

    Определение 3. Функция f(х) называется возрастающей (убывающей)на промежутке [a, b], если для двух любых точек х₁ и х₂ из этого промежутка, таких, что х₁ < х₂ , выполняется неравенство

f(х₁) < f(х₂)  (f(х₁) > f(х₂)).

    Определение 4.Любая возрастающая или убывающая функция называется монотонной.

    Теорема 2.Пусть функция f(х) непрерывна и монотонна на отрезке [a, b] и принимает на его концах значения разных знаков. Тогда внутри отрезка содержится корень уравнения f(х) = 0, и этот корень единственный (рис.2).

    Теорема 3. Если функция f(х) непрерывна на отрезке [a, b], принимает на концах отрезка значения разных знаков и производная f(х) внутри отрезка сохраняет постоянный знак, то внутри отрезка существует корень уравнения f(х) = 0, и притом единственный.

    Рассмотрим графический метод отделения корней.

Т.к. действительные корни уравнения (1) - это точки пересечения графика функции y = F(х) с осью абсцисс, достаточно построить график функции F(х) и отметить на оси Ох отрезки, содержащие по одному корню. Построение графика часто удается упростить, заменив уравнение (1) равносильным уравнением

f₁(х) = f₂(х).                                             (2)

    Построим графики функции f₁(х) и f₂(х), а затем на оси Ох отметим отрезок, на котором содержится абсцисса точки пересечения этих графиков. Рассмотрим

    Пример. Пусть задано уравнение sin 2x - ln x = 0. Это уравнение не является алгебраическим, так как оно содержит трансцендентные функции: логарифмическую и тригонометрическую. Такие уравнения решаются только численно.

    Отделим корни этого уравнения графическим методом. Преобразуем исходное уравнение: sin 2x = ln x.

    Построим графики функций у₁ = sin 2x и у₂ = ln x.

Из графика (рис.3) следует, что исходное уравнение имеет единственный корень x, и он содержится в интервале [1; 1,5]. Говорят, что искомый корень отделен на интервале [1; 1,5].

Рис.3. Иллюстрация к отделению корней графическим методом

Теперь рассмотриманалитический методотделения корней. Покажем, как это делается на конкретном примере. Пусть требуется аналитическим методом отделить корни уравнения

х⁴ – х³ –2х² + 3х – 3 = 0.

f(x) = х⁴ – х³ –2х² + 3х – 3.

Найдем производную f ¢(x) = 4х³ – 3х² – 4х +3.

Найдем её корни: f ¢(x) = 0.

4х³ – 3х² – 4х + 3 = 0,

4х (х² - 1) - 3(х² - 1) = 0,

(х² - 1) (4х - 3) = 0,

х₁ = -1; х₂ = 1; х₃ = 3/4.

В точках х₁, х₂, х₃ функция меняет знак, с учетом этого составим для найденных значений из области определения функции f(x) знаки исходной функции (табл. 2.1).

Таблица 2.1 — Интервалы изменения знаков функции х⁴ – х³ – 2х² + 3х – 3

    Из табл. 2.1 видно, что функция дважды меняет знак, значит, можно утверждать, что она имеет, по меньшей мере, два корня:

х₁ Î [ - ¥; -1] и х₂ Î [1 ; + ¥].

    Сузим эти интервалы, содержащие корни, подбирая такие значения х, при которых сохраняется соответствующий знак функции. Построим табл. 2.2.

Таблица 2.2— Суженные интервалы изменения знаков функции

х⁴ – х³ – 2х² + 3х – 3

    Следовательно, x₁Î[-2; -1] и х₂ Î[1; 2]. Таким образом, мы отделили аналитическим способом два интервала, содержащих корни данного уравнения.

    Для уточнения значений корней следует применить один из методов, которые будут рассмотрены ниже.

    Оба из рассмотренных методов отделения корней не исключают вероятность пропустить корни. Поэтому целесообразно действия подкрепить вычислениями, а именно, следует использовать следующие очевидные положения:

    1) если непрерывная на отрезке [a, b] функция F(x) принимает на его концах значения разных знаков (т.е. F(a) F(b)< 0), то уравнение (1) имеет на этом отрезке, по меньшей мере, один корень;

    2) если функция F(x) к тому же еще и монотонна на интервале [a, b], то корень на отрезке [a, b] единственный.

    Подведем итоги.

    Процесс решения уравнения F(x) = 0 сводится к двум этапам:

    1) отделение корней,

    2) уточнение корней с заданной точностью (ниже мы рассмотрим четыре способа уточнения корней).

    Далее опишем алгоритм отделения корней уравнения F(x) = 0.

Будем считать, что все его корни содержатся на отрезке [А, В], на котором функция определена, непрерывна, и F(А) · F(В) < 0. Требуется отделить все корни уравнения, принадлежащие интервалу [А, В], т.е. указать все отрезки [a, b] Î[А, В], содержащие по одному корню. Для пояснения наших рассуждений начертим рис. 4 .

    Будем вычислять значения F(x), начиная от х = А, двигаясь вправо с некоторым шагом h. Как только обнаружится пара соседних значений F(x), имеющих разные знаки, соответствующие значения аргумента х образуют отрезок, содержащий корень. Далее приведем алгоритма отделения корней. На печать будем выводить значение х₁ – левый конец отрезка, содержащего корень уравнения, и х₂ – правый конец этого отрезка.

Рис.4. Иллюстрация к алгоритму отделения корней уравнения

АЛГОРИТМ ОТДЕЛЕНИЯ КОРНЕЙ УРАВНЕНИЯ

ШАГ 1. Вводим левый конец большого интервала А, правый конец большого интервала В и шаг h.

ШАГ 2. За левый конец малого интервала берем левый конец большого интервала, т.е. х₁ = А, за правый конец малого интервала берем х₂ = х₁ + h.

ШАГ 3. Вычисляем значение функции на левом конце малого интервала, т.е. у₁= F(x₁).

ШАГ 4. Если х₂ < В, то переходим к шагу 5, в противном случае уходим в конец задачи (на шаг 11).

ШАГ 5. Вычисляем значение функции на правом конце малого интервала, т.е. у₂= F(x₂).

ШАГ 6. Если на концах малого интервала значения функции разных знаков (у₁ · у₂ < 0), то выводим на печать х₁ и х₂ (значения левого и правого концов интервала, содержащего корень).

ШАГ 7. В качестве левого конца малого интервала принимаем его правый конец, т.е. х₁ = х₂.

ШАГ 8. Определяем правый конец следующего малого интервала: х₂ = х₁ + h.

ШАГ 9. Перезапоминаем значения функций, т.е. у₁ = у₂.

ШАГ 10. Переход на шаг 4.

ШАГ 11. Конец задачи.

    Замечание. Как можно потерять корни в процессе их отделения?

    Надежность рассмотренного алгоритма отделения корней существенно зависит от характера функции F(х) и выбранной величины шага h. На практике могут возникнуть такие ситуации.

    1. На концах интервала [х, х + h ] функция имеет одинаковые знаки (рис.5). Естественно ожидать, что на этом интервале корней нет. Так можно потерять корни, если не проверять функцию на монотонность.

Рис.5. Во избежание потери корней следует проверять функцию на монотонность (должно быть F(x) ·F(x + h) < 0)

2. Можно пропустить корни на отрезке [х, х+h], даже если соблюдается условие F(x) F(x+h) < 0 (рис. 6). Чтобы избежать такой ситуации, следует h брать достаточно малым.

Рис.6. Во избежание потери корней следует брать h достаточно малым

КОНТРОЛЬНЫЙ ПРИМЕР К АЛГОРИТМУ ОТДЕЛЕНИЯ КОРНЕЙ

        Для уравнения cos x – lg x =0 на отрезке [0,5; 10] отделить интервалы, содержащие изолированные корни.

    ОТВЕТ. Границы интервалов, содержащих искомые корни данного уравнения, таковы:

1,4165 £ х₁ £ 1,4194,

5,5512 £ х₂ £ 5,5532,

6,8622 £ х₃ £ 6,8641.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

    1. В чем заключается процесс построения математической модели?

    2. По какой причине для решения некоторых задач используют численные методы?

    3. Что такое погрешность модели, погрешность метода и вычислительная погрешность?

    4. Что значит «решить уравнение»?

    5. Что значит «отделить корни уравнения»?

    6. Дайте определение функции, непрерывной в точке.

    7. Какая функция называется непрерывной на некотором интервале?

    8. Сформулируйте теорему о существовании корней уравнения.

    9. Какая функция называется возрастающей (убывающей) на некотором промежутке?

    10. Какая функция называется монотонной?

    11. Сформулируйте теорему о существовании единственного корня уравнения.

    12. Опишите процесс отделения корней графическим методом.

    13. В чем заключается аналитический метод отделения корней?

    14. Опишите численный алгоритм отделения корней уравнения.

    14. Как можно потерять некоторые корни уравнения при их отделении?