
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
КОНТРОЛЬНЫЙ ПРИМЕР ДЛЯ МЕТОДА ДИХОТОМИИДля уравнения х - 10 sin x = 0 на интервале [0; 3] уточнить значение корня методом половинного деления с точностью e = 0,01. Ответ : корень х = 2,85. Погрешность Dх =0,00036 УТОЧНЕНИЕ КОРНЕЙ УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ МЕТОДОМ ХОРД Пусть корень x уравнения f (x) = 0 отделен на отрезке [а, b], причем f¢(x) и f ¢¢(x) непрерывны и сохраняют знаки при а £ х £ b. Пусть для определенности f ¢¢(x) > 0 при а £ х £ b. Случай f ¢¢(x) < 0 сводится к рассматриваемому, если записать уравнение в виде -f (x) = 0 .
1) f (a) > 0 (рис.9) 2) f (a) < 0 (рис.10)
Рис. 9. Ситуация, когда f (a) > 0
Рис.10. Ситуация, когда f (a) < 0
Запишем уравнение хорды АВ, проходящей через точки А(а, f (a)) и В(b, f(b)):
Хорде АВ принадлежит точка х1; в ней у = 0. Каждое очередное приближение к корню x находится как точка пересечения хорды АВ с осью абсцисс. Следовательно, можно подставить х = х1 и у = 0 в уравнение хорды. Получим
Выразим отсюда х1 = а – Аналогично можно получить любое приближение хn к корню x. В первом случае (рис.9) неподвижен конец хорды а, и получаем последовательные приближения x0 = b, хn+1 = xn – (xn – a) образующие ограниченную монотонно убывающую последовательность, причем а < x< ... < xn+1 < xn < ... < x1 < x0 =b. Во втором случае (рис.10) неподвижен конец хорды b, и последовательные приближения к корню х0 = a, хn+1 = xn – (b – xn) образующие монотонно возрастающую последовательность, причем  а = x0 < x1 < x2 < ...<xn< xn+1 <...< x < b. Подведем итоги: 1) неподвижен тот конец хорды, для которого знак f (x) совпадает со знаком второй производной f ¢¢(x); 2) последовательные приближения к корню хn лежат по ту сторону корня x, где функция f (х) имеет знак, противоположный знаку ее второй производной f ¢¢(x). В обоих случаях каждое следующее приближение хn+1 ближе к корню x, чем предшествующее хn; 3) для оценки точности приближения можно воспользоваться формулой ½хn – xn–1½< e , где e – заданная предельная абсолютная погрешность, т.к. в этом случае гарантировано, что ½x - xn½< e , Теперь можно сформулировать алгоритм метода хорд. АЛГОРИТМ МЕТОДА ХОРД ШАГ 1. Вводим концы интервала, содержащего корень уравнения и требуемую точность вычислений, а - левый конец интервала, b - правый конец интервала, e - точность. ШАГ 2. Вычисляем значение функции f(x) на левом конце интервала, содержащего корень, т.е. F1 = f(a). ШАГ 3. Вычисляем значение функции f(x) на правом конце интервала, содержащего корень, т.е. F2 = f(b). ШАГ 4. Вычисляем значение 2-й производной (взятой предварительно вручную) в середине отрезка, содержащего корень: F3 = f ¢¢((b - a)/2). ШАГ 5. Организуем счетчик числа приближений; сначала N =0. ШАГ 6. Выясняем, какой конец хорды неподвижен. Для этого проверяем знак произведения F1·F3. Для удобства реализации этого момента в программе введем признак р, который будет принимать некоторые фиксированные значения, например, 1 или 2, в зависимости от того, какой конец хорды неподвижен. Если знак F1 · F3 положителен, то неподвижен конец хорды а, и следует положить х0 = b, р = 2, в противном случае, т.е. когда знак произведения отрицателен, неподвижен конец хорды b и следует положить х0 = а, р = 1. ШАГ 7. Вычисляем значение f (x) в найденной точке х0: F4 = f (х0). ШАГ 8. Определяем, по какой формуле вычислять следующее приближение к корню хn+1. Если р = 1, то используем формулу (4), если р = 2, то (3). ШАГ 9. Выводим на печать текущее значение N, х0, F4, хN+1. ШАГ 10. Увеличиваем номер приближения на 1, т.е. N = N+1. ШАГ 11. Если абсолютная величина разности между х0 и х1 стала меньше e, т.е. если ½х1 - x0½< e, то выводим на печать текущее значение приближения x0 и полученное значение х1, которое и будет искомым значением корня, после чего переходим на ШАГ 12. В противном случае, когда ½хn - xn–1½> e , в качестве х0 берем х1 , т.е. х0 = х1, и переходим на шаг 7. ШАГ 12. Конец задачи.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 208. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 При f ¢¢(x) > 0 кривая выпукла вниз. Если провести хорду АВ, то кривая будет лежать ниже хорды. При этом возможны два случая:
При f ¢¢(x) > 0 кривая выпукла вниз. Если провести хорду АВ, то кривая будет лежать ниже хорды. При этом возможны два случая:

 .
.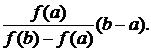
 n=0,1,2… (3)
n=0,1,2… (3)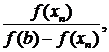 n=0,1,2… (4)
n=0,1,2… (4)