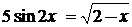Студопедия

КАТЕГОРИИ:

АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Для закрепления изученного материала следует выполнить практическое задание  №1.     

⇐ ПредыдущаяСтр 2 из 7Следующая ⇒

ПРАКТИЧЕСКОЕ ЗАДАНИЕ  № 1

Отделение изолированных корней уравнения «вручную» и с помощью компьютерной программы

Варианты к практическому заданию

Задание 1. Даны два уравнения с одним неизвестным. Для первого из них отделить корни графическим способом, для второго – аналитическим.

Вариант

Уравнения
1 1. 0,5х +1 = (х–2)2 2. 3х4+ 4х3 –12х2 –5 = 0
2 1. х2 – 2 + 0,5х = 0 2. х4 – х – 1 = 0
3 1. 0,5х – 1 = (х+1)2 2. х4 +4х3 – 8х2 – 17 = 0
4 1. (х – 2)2 · 2х = 1 2. 3х4 +4х3 – 12х2+1 = 0
5 1. х2 – 3 + 0,5х = 0 2. х4 – 4х3 – 8х2 + 1 = 0
6 1. (х – 1)2 ·2х = 1 2. х4 – 3х – 1 = 0
7 1. 2х2 – 0,5х – 3 = 0 2. х4 – х3 – 2х2 + 3х – 3 = 0
8 1. х2 ·2х = 1 2. х4 – 19х2 + 6 = 0
9 1. 0,5х – 3 = (х + 2)2 2. 2х4 – х2 – 10 = 0
10 1. (х – 3)2 · 2х = 1 2. х4 – 20х2 + 6 = 0
11 1. х2 – 4 + 0,5х = 0 2. 3х4 – 8х3 – 18х2 + 2 = 0
12 1. 0,5х – 3 = –(х + 1)2 2. 2х4 – х2 – 11 = 0
13 1. (х – 2)2 · 2х = 1 2. х4 – 21х2 + 6 = 0
14 1. 2х2 – 0,5х – 5 = 0 2. х4 + 8х3 + 6х2 – 10 = 0
15 1. 2х2 – 0,5х – 6 = 0 2. х4 – х – 1 = 0
16 1. 0,5х +1 = (х–2)2 2. 3х4+ 4х3 –12х2 –5 = 0
17 1. х2 – 2 + 0,5х = 0 2. х4 – 2х – 1 = 0
18 1. 0,5х – 1 = (х+1)2 2. х4 +4х3 – 8х2 – 17 = 0
19 1. (х – 4)2 · 2х = 1 2. 3х4 +4х3 –12х2 + 1 = 0
20 1. х2 – 3 + 0,5х = 0 2. х4 – 4х3 – 8х2 + 1 = 0
21 1. (х – 5)2 ·2х = 1 2. х4 – 4х – 1 = 0
22 1. 2х2 – 0,5х – 1 = 0 2. х4 – х 3 – 2х2 + 3х – 3 = 0
23 1. х2 ·2х = 1 2. х4 – 18х2 + 6 = 0
24 1. 0,5х – 3 = (х + 2)2 2. 2х4 – х2 – 13 = 0
25 1. (х – 7)2 · 2х = 1 2. х4 – 17х2 + 6 = 0
26 1. х2 – 4 + 0,5х = 0 2. 3х4 – 8х3 – 18х2 + 2 = 0
27 1. 0,5х – 3 = –(х + 1)2 2. 2х4 – х2 – 12 = 0
28 1. (х – 8)2 · 2х = 1 2. х4 – 16х2 + 6 = 0
29 1. 2х2 – 0,5х – 2 = 0 2. х4 + 8х3 + 6х2 – 11 = 0
30 1. 2х2 – 0,5х – 4 = 0 2. х4 – 5х – 1 = 0

Задание 2.Отделить изолированные корни уравнения с помощью компьютерной программы.

    Написать программу, которая на заданном отрезке [A; B] отделяет интервалы, содержащие корни заданного уравнения. Программа должна печатать номер корня, левый конец интервала, содержащего корень, и правый конец интервала, содержащего корень. Если в условии значения А и В не указаны, можно брать любые числа из области определения функции.

Вариант Уравнение Интервал
1 (0,2 х)3 = cos x  
2 х – 10 sin x = 0  
3 2–x = sin x При х < 10
4 2х – 2 cos x = 0 При х > –10
5 lg (x + 5) = cos x При х > –5
6  
7 x sin x – 1 = 0 На отрезке [–10; 10]
8 7 cos x – x = 6  
Вариант Уравнение Интервал
9 sin x – 0,2 x = 0  
10 10 cos x – 0,1 x2 = 0  
11 2 lg (x + 7) – 5 sin x = 0  
12 4 cos x + 0,3 x = 0  
13  
14 2 x2 – 5 = 2x  
15 2–x = 10 – 0,5 x2  
16 (0,2 х) 3 = cos x  
17 х – 9 sin x = 0  
18 3–x = sin x При х < 10
19 2х – 3 cos x = 0 При х > –10
20 lg (x + 3) = cos x При х > –3
21  
22 x sin x – 1 = 0 На отрезке [–10; 10]
23 8 cos x – x = 6  
24 sin x – 0,2 x = 0  
25 10 cos x – 0,1 x2 = 0  
26 2 lg (x + 7) – 4 sin x = 0  
27 4 cos x + 0,5 x = 0  
28  
29 2 x2 – 7 = 2x  
30 2–x = 9 – 0,5 x2  

 


ЛЕКЦИЯ 2

УТОЧНЕНИЕ КОРНЕЙ УРАВНЕНИЯ С ЗАДАННОЙ ТОЧНОСТЬЮ МЕТОДОМ ПОЛОВИННОГО ДЕЛЕНИЯ (МЕТОДОМ ДИХОТОМИИ)

Прежде, чем перейти к описанию методов уточнения корней, дадим определение.

Определение 5.Будем говорить, что корень x уравнения F(x) = 0 вычислен с заданной точностью e, если ½x - x1½£ e , где x1 - приближенное значение корня.

Пусть уравнение (1) имеет на отрезке [a, b] единственный корень. Функция F(x) на этом отрезке пусть будет непрерывна. Разделим отрезок [a, b] пополам точкой с = (а + b)/2. Если F(c) ¹ 0 (что очень вероятно), то возможны два случая:

 

 

 


Рис.7. Функция меняет знак на отрезке [а, с]

 

 


          

  

      

   

            

Рис.8.Функция меняет знак на отрезке [с, b]

  а) F(x) меняет знак на отрезке [а, с] (рис. 7),

    б) F(x) меняет знак на отрезке [с, b] (рис. 8).

    Выбираем тот из отрезков, на котором функция меняет знак, а значит, на нем содержится корень функции. Этот отрезок снова делим пополам, снова проверяем знаки функции на концах полученных отрезков и так дойдем до сколь угодно малого отрезка, содержащего корень уравнения (1).

    Дихотомию можно использовать как метод решения уравнения с заданной точностью. Если на каком-то этапе получен отрезок [a, b], содержащий корень, то за значение корня можно принять х = (a+b)/2. Ошибка при этом не превысит Dх = (b - a)/2.

Далее приведем алгоритм метода половинного деления.

АЛГОРИТМ МЕТОДА ПОЛОВИННОГО ДЕЛЕНИЯ

    ШАГ 1. Вводим концы интервала, содержащего корень уравнения и требуемую точность вычислений, а - левый конец интервала, содержащего корень, b - правый конец интервала, содержащего корень, e - точность вычислений.

    ШАГ 2. Вычисляем координату середины отрезка, а именно

с = (а + b)/2.

    ШАГ 3. Определяем интервал, на котором функция меняет знак. Для этого вычисляем значения функции в точках, например, а и с и выясняем знак их произведения. Если он отрицателен, значит, на этом отрезке функция сменила знак, тогда в качестве правого конца отрезка берем значение с (рис.7), в противном случае значение с берем в качестве левого конеца отрезка (рис.8). Другими словами, если F(a) · F(с) < 0 , то b = с, в противном случае а = с.

    ШАГ 4 . Если ½b-а½ > e, то переходим к шагу 2, в противном случае переходим на ШАГ 5.

    ШАГ 5. Вычисляем приближенное значение корня х = (а + b)/2 и погрешность вычислений Dх = (а - b)/2.

    ШАГ 6. Печатаем х и Dх.

    ШАГ 7. Конец задачи.

Число шагов N @ log2 ((b–a)/e) при использовании дихотомии велико, поэтому сходимость медленная, но при любой длине отрезка она гарантирована. Однако простота реализации метода уменьшает число вспомогательных операций и частично компенсирует увеличение общего времени счета из-за медленной сходимости.




⇐ Предыдущая1234567Следующая ⇒






Последнее изменение этой страницы: 2018-06-01; просмотров: 245.

stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда...