
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исследование чувствительности целевой функции ⇐ ПредыдущаяСтр 6 из 6 В предыдущем пункте было проведено качественное исследование оптимального решения. Никаких цифр, которые показывали бы, как влияют правые части ограничений на оптимальное значение целевой функции, получено не было. Получение таких цифр требует более тонкого математического анализа. Основой для их получения в линейном программировании является следующая теорема: если оптимальное решение x* задачи линейного программирования не вырождено, то Здесь L(x*) – значение целевой функции на оптимальном плане; Как известно, физическая интерпретация производной – скорость. Поэтому Таким образом, для исследования чувствительности целевой функции к изменениям правых частей основных ограничений необходимо найти оптимальный двойственный план (4.2) и исследовать его компоненты. Согласно таблице 3.11 базисными являются переменные x1, x2, x4, x7. Поэтому
Вычислим обратную базисную матрицу
и найдем оптимальный двойственный план
Дадим экономическую интерпретацию полученным результатам. 1-ое ограничение является количественным и связано с наличием заказа на подготовку специалистов по специальности ЭВМ. Это ограничение является существенным, увеличение заказа на 1-го специалиста приводит к уменьшению дохода вуза на  2-ое ограничение является количественным и связано с наличием заказа на подготовку специалистов по специальности ПО. Это ограничение также является существенным, увеличение заказа на 1-го специалиста приводит к уменьшению дохода вуза на 3-ое ограничение, как и два предыдущих, является количественным и связано с ограничением министерства образования на подготовку специалистов на заочной форме обучения. Это ограничение является несущественным, а поэтому целевая функция нечувствительна к его изменению( 4-ое ограничение является ресурсным и связано с объемом финансирования. Этот ресурс является дефицитным. Увеличение финансирования на 1 млн. рублей приводит к возрастанию целевой функции на Выводы, полученные на основе анализа оптимального двойственного плана, полностью соответствуют выводам, сделанным в ходе предварительного анализа оптимального решения.
Исследование устойчивости оптимального базисного плана В соответствии с п. 4.2, изменяя правые части системы ограничений, можно добиться улучшения оптимального значения целевой функции. Однако со значениями правых частей напрямую связан оптимальный план: изменяем количество ресурсов (объем заказов) – изменяется план производства (в нашем случае – план подготовки специалистов). При больших изменениях в наличии ресурсов возможны значительные изменения в оптимальном плане производства: выпуск одних видов продукции придется свернуть, других – наладить. Изменение в структуре производства крайне нежелательны. Как правило, они влекут дополнительные финансовые затраты: на переналадку оборудования, на переобучение персонала и т.п. Поэтому возникла проблема устойчивости оптимального решения к изменениям правых частей ограничений: в каких пределах можно изменять правые части ограничений, чтобы структура оптимального плана не изменилась. Под структурой оптимального плана понимается состав его базисных (ненулевых) и небазисных (нулевых) компонент. В экономической интерпретации эту проблему можно сформулировать так: в каких пределах можно управлять запасами ресурсов (объемами заказов), чтобы при этом не изменилась структура производства? Предположим, что правая часть i-го ограничения bi изменилась на величину Θ, т.е. стала равной bi+Θ, где zi– i-ый столбец обратной базисной матрицы Назовем диапазон возможных значений величины bi интервалом устойчивости к изменениям правой части i-го ограничения и обозначим где |
|||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 322. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (4.1)
(4.1)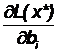 - частная производная целевой функции по переменной bi; yi* - i-ая компонента оптимального двойственного плана, который находится из соотношения
- частная производная целевой функции по переменной bi; yi* - i-ая компонента оптимального двойственного плана, который находится из соотношения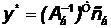 . (4.2)
. (4.2)
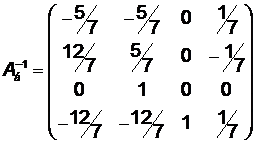
 .
. млн. рублей и, наоборот, уменьшение заказа на 1-го специалиста приводит к увеличению дохода на
млн. рублей и, наоборот, уменьшение заказа на 1-го специалиста приводит к увеличению дохода на  млн. рублей.
млн. рублей. ).
). млн. рублей.
млн. рублей. - соответствующий (новый) оптимальный план. Связь между старым x* и новым
- соответствующий (новый) оптимальный план. Связь между старым x* и новым  , (4.3)
, (4.3) . Равенство (4.3) вместе с прямым ограничением
. Равенство (4.3) вместе с прямым ограничением  дает ответ на поставленную выше проблему: величина изменения правой части i-го ограничения Θ должна быть такой, чтобы выполнялось неравенство:
дает ответ на поставленную выше проблему: величина изменения правой части i-го ограничения Θ должна быть такой, чтобы выполнялось неравенство: (4.4)
(4.4) . Тогда из неравенства (4.4) вытекает следующее соотношение:
. Тогда из неравенства (4.4) вытекает следующее соотношение: , (4.5)
, (4.5) - максимально возможное уменьшение,
- максимально возможное уменьшение,  - максимально возможное увеличение правой части i-го ограничения. При этом
- максимально возможное увеличение правой части i-го ограничения. При этом