
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПОСТАНОВКА И ОБЩАЯ СХЕМА РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯСтр 1 из 6Следующая ⇒ МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «БРЕСТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра информатики и прикладной математики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ к курсовой работе «РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ» по дисциплине «Системный анализ и исследование операций» для студентов специальности «Автоматизированные системы обработки информации» дневной и заочной форм обучения
БРЕСТ 2006 УДК 519.816
Пособие представляет собой руководство по выполнению курсовой работы по дисциплине «Системный анализ и исследование операций» для студентов специальности 1-53 01 02 «Автоматизированные системы обработки информации». В пособии приводятся: общая схема решения оптимизационной задачи; примеры построения математических моделей; пример решения задачи линейного программирования с послеоптимизационным анализом и поиском целочисленного решения; варианты заданий для выполнения курсовой работы; требования к содержанию и оформлению курсовой работы.
Составитель: В.М. Ракецкий, доцент, к.ф.-м.н.
Рецензент: В.М. Мадорский, доцент кафедры информатики и прикладной математики Брестского государственного университета им. А.С. Пушкина, к.ф.-м.н.
Учреждение образования ©«Брестский государственный технический университет», 2006
СОДЕРЖАНИЕ BВЕДЕНИЕ.. 4 1. ПОСТАНОВКА И ОБЩАЯ СХЕМА РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 6 2. ПРИМЕРЫ ФОРМАЛИЗАЦИИ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.. 9 2.1. Задача о распределении ресурсов (или производственная  2.2. Задача о загрузке оборудования. 10 2.3. Задача о рационе. 11 2.4. Задача о раскрое. 12 2.5. Задача о смеси.. 13 2.6. Транспортная задача. 13 3. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.. 15 3.1. Постановка задачи.. 15 3.2. Построение математической модели.. 15 3.3. Решение задачи.. 17 4. ПОСЛЕОПТИМИЗАЦИОННЫЙ АНАЛИЗ РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.. 27 4.1. Предварительный анализ оптимального решения. 27 4.2. Исследование чувствительности целевой функции.. 27 4.3. Исследование устойчивости оптимального базисного плана. 29 5. ПОИСК ОПТИМАЛЬНОГО ЦЕЛОЧИСЛЕННОГО РЕШЕНИЯ.. 33 6. ВАРИАНТЫ ЗАДАНИЙ.. 38 7. ТРЕБОВАНИЯ К СОДЕРЖАНИЮ И ОФОРМЛЕНИЮ КУРСОВОЙ РАБОТЫ... 75 7.1. Содержание курсовой работы... 75 7.2. Требования к оформлению курсовой работы... 76 ЛИТЕРАТУРА.. 79 ПРИЛОЖЕНИЕ.. 80
BВЕДЕНИЕ
В настоящем пособии рассматривается материал, необходимый для выполнения курсовой работы по дисциплине «Системный анализ и исследование операций» для студентов специальности 1-53 01 02 «Автоматизированные системы обработки информации». В любом операционном исследовании реализуются следующие основные этапы: 1) постановка задачи оптимизации; 2) построение математической модели; 3) поиск оптимального решения; 4) проверка и корректировка модели; 5) реализация оптимального решения на практике. Этапы 2 и 3 операционного исследования можно выполнить с использованием математического программирования, объектом исследования которого являются экстремальные задачи при наличии ограничений. Слово «программирование» в названии «математическое программирование» отражает тот факт, что результатами математических исследований являются не только качественные результаты – леммы, теоремы, критерии, но и конструктивные – методы (алгоритмы) решения конкретных задач, возникающих на практике. Поскольку круг прикладных экстремальных задач чрезвычайно широк, в математическом программировании возникли собственные направления, связанные с исследованием специальных классов оптимизационных задач: линейных, нелинейных, динамических, дискретных (целочисленных), стохастических и т.п. Наиболее развитым и законченным разделом математического программирования является линейное программирование, когда в задачах оптимизации находится экстремум линейной целевой функции при линейных ограничениях. Хотя такие задачи являются наиболее простыми из оптимизационных задач, они имеют многочисленные применения в экономике и технике, сфера приложения которых постоянно расширяется. Поэтому линейное программирование, являясь основой современного математического программирования, не представляет нечто застывшее, оно развивается, пополняется новыми методами. В теории линейного программирования доказано, что экстремум целевой функции всегда достигается в угловых точках многогранника допустимых решений. Поэтому решение задачи линейного программирования, в принципе, можно найти перебором угловых точек этого многогранника. Эта простая идея легко реализуется при 2-х, максимум 3-х, переменных (графический метод решения задачи линейного программирования). В общем случае к решению задачи линейного программирования вплотную подошел в 30-40 годах прошлого века советский экономист и математик, лауреат Нобелевской премии Канторович Л.В. Однако довести исследования до алгоритма решения впервые удалось в 1947 г. американскому ученому Дж. Данцигу. Он предложил метод, который стал широко известен под названием «симплекс-метод». Симплекс-метод (СМ) представляет собой процедуру целенаправленного перебора угловых точек (в СМ их называют базисными планами), когда от одной точки к другой переходят только в том случае, если значение целевой функции, по крайней мере, не ухудшается. Для того чтобы «запустить» СМ, необходимо найти начальный базисный план (в ряде случаев он находится достаточно просто). Сам симплекс-метод представляет собой итерационную процедуру, состоящую из 3-х элементов: 1) выполняется оценка оптимальности базисного плана и, если он не оптимален, выбирается направление (ребро, если говорить о многограннике) для перехода к следующему базисному плану; 2) рассчитывается максимально допустимый шаг вдоль выбранного направления; 3) осуществляется переход к новому базисному плану. В настоящее время решают линейные задачи с десятками тысяч переменных и тысячами ограничений. В методических указаниях рассматривается общая схема решения оптимизационных задач (разд. 1), приводятся примеры построения различных математических моделей (разд. 2). Подробно рассмотрен пример решения задачи линейного программирования, который включает: · постановку, построение математической модели и решение нецелочисленной задачи (разд. 3); · послеоптимизационный анализ полученного решения (разд. 4); · нахождение оптимального целочисленного решения (разд. 5). Для выполнения курсовой работы предлагается пакет заданий по решению оптимизационных задач, включающий 104 варианта заданий (разд. 6), излагаются требования по выполнению и оформлению курсовой работы по проблематике линейного программирования (разд. 7). Рекомендуемая студентам литература включает источники по исследованию операций и линейному программированию [1-17]. ПОСТАНОВКА И ОБЩАЯ СХЕМА РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Математическое программирование рассматривает задачи оптимизации. Сущность таких задач можно выразить следующим образом: определить значения переменных x1, x2,…,xn, которые обеспечивают экстремум функции L(x1, x2,…,xn) с учетом ограничений, наложенных на аргументы этой функции – переменные x1, x2,…,xn ( элементы решения ). Функция L, для которой определяется экстремум, называется целевой функцией. Содержательный смысл переменных x1, x2,…,xn и целевой функции L полностью зависит от решаемой задачи. Среди задач математического программирования наиболее изучены задачи линейного программирования, в которых целевая функция L линейно зависит от элементов решения x1, x2,…,xn, а ограничения, накладываемые на элементы решения, имеют вид линейных равенств или неравенств относительно x1, x2,…,xn. Таким образом, в задачах линейного программирования находится экстремум линейной целевой функции при линейных ограничениях. Задача линейного программирования в общей форме формулируется следующим образом: найти значения переменных x1, x2,…,xn, которые доставляют максимальное (минимальное) значение целевой функции и удовлетворяют системе ограничений Здесь n – количество переменных, m - общее количество ограничений, знак В некоторых задачах на все или некоторые переменные может накладываться требование целочисленности. Формулировка задачи (1.1) , (1.2) представляет собой математическую модель задачи, или постановку задачи линейного программирования в общей форме. Допустимое решение задачи линейного программирования – это набор значений переменных x1, x2,…,xn, удовлетворяющих условиям (1.2). Исторически сложилось, что допустимое решение задачи линейного программирования называют планом. Множество всех планов называется областью допустимых решений (ОДР). Оптимальное решение – это такой план, который максимизирует (или минимизирует) функцию (1.1). Обычно задача линейного программирования имеет бесконечное множество всех планов и единственный оптимальный план. Решение задачи линейного программирования состоит в нахождении оптимального плана. Основной метод решения задач линейного программирования – симплекс-метод. Для решения задачи этим методом она должна быть приведена к канонической форме. В этой форме задачи все переменные должны быть неотрицательны, все ограничения имеют вид равенств: При сведении задачи, заданной в общей (произвольной) форме (1.1), (1.2), к канонической форме (1.3) количество переменных, как правило, изменяется, поэтому значения n для (1.1), (1.2) и (1.3) обычно разные. Для приведения задачи к канонической форме требуется привести ограничения-неравенства к ограничениям-равенствам. Для перехода от ограничений-неравенств к равенствам вводятся дополнительные (свободные) переменные. Такие переменные вычитаются из левых частей ограничений «не меньше» и прибавляются к левым частям ограничений «не больше». Общая схема решения задач линейного программирования с использованием симплекс-метода следующая: 1. По содержательной постановке задачи строится ее математическая модель в общей форме. 2. Задача приводится к канонической форме (1.3). 3. Если система основных ограничений задачи (1.3) находится в предпочтительном виде, то выполняется переход к шагу 7. Обычно это возможно для задач, в постановке которых имеются только ограничения вида «не больше». 4. Строится вспомогательная задача линейного программирования. 5. C помощью симплекс-метода находится решение вспомогательной задачи и, тем самым, начальный базисный план исходной задачи. 6. Производится переход от вспомогательной задачи линейного программирования к исходной (в задачу возвращается исходная целевая функция). 7. С помощью симплекс-таблиц находится оптимальный план исходной задачи. 8. Выполняется анализ на чувствительность, т. е. анализ зависимости результатов от изменений в постановке задачи (если это требуется). 9. Находятся интервалы устойчивости оптимального решения к изменениям правых частей. 10. Находится целочисленное решение (если это требуется по содержанию задачи). Для этого применяется метод ветвей и границ или метод Гомори. 11. Производится интерпретация результатов решения задачи, т. е. определяется их содержательный смысл.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 287. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1.1)
(1.1) (1.2)
(1.2) обозначает одну из операций отношения
обозначает одну из операций отношения 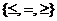 .
. (1.3)
(1.3)