
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Постановка задачи Высшее учебное заведение занимается подготовкой специалистов по 2-м специальностям. В соответствии с имеющимся портфелем заказов необходимо каждый год выпускать не менее 200 специалистов по специальности «Проектирование и производство ЭВМ» (кратко - ЭВМ) и 300 специалистов по специальности «Проектирование и разработка программного обеспечения» (кратко ПО). Подготовка специалистов может вестись по двум формам обучения: дневной и заочной. По требованию министерства образования количество студентов заочной формы обучения не должно превышать 150 человек. За подготовку одного специалиста на дневной форме обучения вуз получает 12 млн. рублей, на заочной - 5 млн. рублей. Затраты на подготовку специалиста при дневной форме обучения составляют 8,8 млн. рублей на специальности ЭВМ и 8,5 млн. рублей на специальности ПО. При заочной форме обучения эти затраты составляют 4,5 млн. рублей на специальности ЭВМ и 4,0 на специальности ПО. Объем финансирования составляет 5500 млн. рублей в год. Составить план подготовки специалистов, при котором доходы вуза будут максимальными.
3.2. Построение математической модели Процесс подготовки специалистов с высшим образованием является долговременным и занимает 4 и более лет. Некоторые из студентов в процессе обучения уходят в академические отпуска, отчисляются и т.п. Однако в постановке задачи отсутствует информация, позволяющая учесть изменение числа студентов от курса к курсу. Поэтому будем предполагать, что число тех студентов, которые поступают на учебу, совпадает с количеством выпускников. Это предположение позволяет рассматривать не общее количество студентов в вузе, а количество студентов, обучающихся на одном курсе. Введем переменные, которые требуется определить:  x1 - количество студентов специальности ЭВМ дневной формы обучения; x2 - количество студентов специальности ЭВМ заочной формы обучения; x3 - количество студентов специальности ПО дневной формы обучения; x4 - количество студентов специальности ПО заочной формы обучения. Тогда x1+ x2 – общее количество студентов специальности ЭВМ,
Учтем ограничение, установленное министерством образования на количество студентов заочной формы обучения. x2+ x4 – общее количество студентов заочной формы обучения. Поэтому
Стоимость подготовки специалистов составит
Очевидно, что все переменные в задаче неотрицательны: xj ≥ 0, j = 1,...,4 Суммы, выплачиваемые вузу за подготовку специалистов, а также затраты вуза на их подготовку, известны. Поэтому можно подсчитать доход вуза от подготовки одного специалиста. Он составляет: § 12 - 8,8 = 3,2 млн. рублей за подготовку на специальности ЭВМ при дневной форме подготовки; § 5 – 4,5 = 0,5 млн. рублей за подготовку на специальности ЭВМ при заочной форме подготовки; § 12 - 8,5 = 3,5 млн. рублей за подготовку на специальности ПО при дневной форме подготовки; § 5 – 4,0 = 1,0 млн. рублей за подготовку на специальности ПО при заочной форме подготовки; Поэтому суммарный доход вуза от подготовки всех специалистов будет равен 3,2x1 + 0,5x2 + 3,5x3 + x4 млн. рублей. Так как доход необходимо максимизировать, то целевую функцию в нашей задаче можно записать так: L =3,2x1 + 0,5x2 + 3,5x3 + x4 → min. Таким образом, математическая модель задачи имеет вид:
Решение задачи Для решения задачи необходимо привести ее математическую модель к канонической форме. Для этого в ограничения ( 3.1) добавим свободные переменные со знаком “-“, а в ограничения (3.2) - свободные переменные со знаком “-“. В результате получим:
Как видно, 3-е и 4-ое ограничения задачи находятся в предпочтительном виде, т. к. в них содержатся переменные, входящие только в одно уравнение и имеющие коэффициент 1 (это переменные x7 и x8). В 1-м и 2-м уравнениях таких переменных нет, т. е. система ограничений не находится в предпочтительном виде. Значит, для решения задачи требуется применить 2-хфазный симплекс-метод. Построим вспомогательную задачу линейного программирования. Для этого в 1-е и 2-е уравнения введем фиктивные переменные x9 и x10. Система ограничений после этого будет выглядеть следующим образом:
Целевая функция вспомогательной задачи представляет собой сумму фиктивных переменных, которую необходимо минимизировать: W =x9 + x10 → min. Начальный базис вспомогательной задачи составляют переменные: 1) в ограничениях, которые находятся в предпочтительном виде, - те переменные, которые обеспечили предпочтительность этих ограничений (в нашем случае это переменные x7, x8); 2) в ограничениях, которые не находятся в предпочтительном виде, - фиктивные переменные (в нашей задаче – переменные x9, x10). Разрешим систему ограничений относительно базисных переменных:
Выразим целевую функцию вспомогательной задачи через небазисные переменные: W = x9 + x10 = 200-x 1-x2+x5+300-x3-x4+x6 = 500-x1-x2-x3-x4+x5+ x6 . Таким образом, вспомогательная задача в симплексной форме будет иметь следующий вид: W = 500-x1-x2-x3-x4+x5+ x6 → min,
Перенесем коэффициенты симплексной формы (3.5) в симплексную таблицу и приступим к решению задачи: Таблица 3.1
Этой симплексной таблице соответствует начальный базисный план вспомогательной задачи:
Этот план не оптимален, так как целевая функция вспомогательной задачи на минимум, а среди коэффициентов целевой функции (строка W вспомогательной задачи) есть отрицательные. Из отрицательных коэффициентов целевой функции необходимо выбрать максимальный по модулю. Поскольку все отрицательные коэффициенты одинаковы, то можем выбрать любой из них, например, в столбце x1. Столбец x1 объявляем ведущим. Рассчитаем максимально допустимый шаг Θ0 вдоль ведущей переменной x1. Для этого в симплексную таблицу добавим столбец, в который будем заносить результаты расчета шага для каждой базисной переменной. Словами правило расчета можно сформулировать следующим образом: если коэффициент в ведущем столбце больше либо равен нулю, то соответствующий шаг равен бесконечности; иначе он равен отношению соответствующего значения в столбце β к значению в ведущем столбце, взятому с противоположным знаком. Максимально допустимый шаг Θ0 вдоль ведущей переменной равен наименьшему из найденных шагов. Формально это правило можно записать с помощью следующих соотношений
Здесь Θi - шаг, рассчитанный по i-ой строке таблицы; βi , ri – элементы i-ой строки таблицы, находящиеся соответственно в столбце β и ведущем столбце таблицы. Если Θ0=∞, то целевая функция неограниченно возрастает (или убывает) на множестве планов задачи. Ее решение в этом случае окончено. Допустим, что Θ0<∞. Строка, содержащая максимально допустимый шаг Θ0 (т.е. содержащая наименьшее из найденных чисел), называется разрешающей. Результаты вычисления максимально допустимого шага для рассматриваемого примера приведены в табл. 3.2. Серым цветом в этой таблице выделены ведущий столбец и разрешающая строка. Элемент, находящийся на пересечении ведущего столбца и разрешающей строки, называется разрешающим. Таким образом, переменная x9 покидает базис, вместо нее в базис вводится ведущая переменная x1. Эта операция сопровождается пересчетом симплексной таблицы, который осуществляется по следующим четырем правилам: Таблица 3.2
1) «новый» разрешающий элемент есть число, обратное к «старому» разрешающему элементу, т.е.
Здесь 2) «новые» элементы разрешающей строки получаются из «старых» элементов делением на «старый» разрешающий элемент, взятый с противоположным знаком, т.е.
Здесь 3) «новые» элементы ведущего столбца получаются из «старых» элементов делением на «старый» разрешающий элемент, т.е.
Здесь 4) Рассмотрим произвольный элемент таблицы, не находящийся ни в ведущем столбце, ни в разрешающей строке. Обозначим его, например, q. Найдем его проекции на ведущий столбец и разрешающую строку. Обозначим их соответственно t и s (см. рисунок ниже).
Пусть
Эту формулу называют правилом прямоугольника. Словами его можно сформулировать так: «новый» элемент симплексной таблицы есть разность между его старым значением и произведением проекций, разделенным на разрешающий элемент. Применим сформулированные выше правила к рассматриваемому примеру. В результате получим таблицу Таблица 3.3
Поскольку фиктивная переменная x9 покинула базис, ее значение стало равным нулю. Это означает, что она выполнила свою функцию и ее можно исключить из дальнейшего рассмотрения, а соответствующий столбец – из таблицы: Таблица 3.4
Таким образом, получено новое базисное решение вспомогательной задачи:
Это решение не является оптимальным решением вспомогательной задачи, т.к. по-прежнему в строке W содержатся отрицательные коэффициенты. Выполняем очередную итерацию. Столбец x3 объявляем ведущим, по результатам расчета максимально допустимого шага получаем, что разрешающей будет строка x8: Таблица 3.5
Переменная x8 покидает базис, вместо нее в базис вводится переменная x3. Однако количество столбцов в новой таблице не уменьшится: переменная x8 – свободная, а не фиктивная. В отличие от фиктивной свободная переменная такая же равноправная переменная, как и x1 – x4, и поэтому не покидает таблицу после вывода из базиса. После пересчета симплексной таблицы получим: Таблица 3.6
Симплексной табл. 3.6 соответствует базисный план вспомогательной задачи
Этот план по-прежнему не оптимален. Столбец x2 выберем в качестве ведущего и рассчитаем максимально допустимый шаг: Таблица 3.7
На основании результатов расчета максимально допустимого шага определяем разрешающую строку x10. После замены в базисе переменной x10 на переменную x2, пересчета симплексной таблицы и исключения переменной x10 из дальнейшего рассмотрения, получим таблицу: Таблица 3.8
Как видно, все искусственные переменные покинули базис и исключены из таблицы. Строка вспомогательной целевой функции W содержит одни нули. Это означает, что решение вспомогательной задачи окончено, первая фаза двухфазного метода завершена, получен базисный план исходной задачи:
Так как все фиктивные переменные покинули задачу, то система основных ограничений вспомогательной задачи совпадает с исходной системой основных ограничений. Искусственная целевая функция с исчезновением фиктивных переменных трансформировалась в нулевую. Поэтому для перехода ко второй фазе симплекс-метода необходимо вернуться к исходной целевой функции. Поскольку исходная целевая функция содержит базисные переменные, их необходимо исключить, выразив через небазисные переменные. С этой целью из последней симплексной таблицы выпишем соотношения, связывающие базисные переменные с небазисными:
Подставляя в исходную целевую функцию вместо переменных x1, x2, x4 соответствующие выражения, получим:
В результате симплексная таблица примет вид: Таблица 3.9
Из таблицы следует, что план x(2) не оптимален, так как среди коэффициентов целевой функции есть отрицательные. Выберем переменную x4 в качестве ведущей и рассчитаем максимально допустимый шаг: Таблица 3.10
Переменная x2 покидает базис, ее заменяет переменная x4. После пересчета таблицы получим: Таблица 3.11
Поскольку строка L таблицы не содержит отрицательных элементов, то базисный план
является оптимальным. Решение задачи окончено. Получено оптимальное решение. Значения основных переменных задачи x1=200, x3= § 200 студентов специальности ЭВМ дневной формы обучения; § § При этом доход вуза составит Естественно, требуется найти целочисленной решение, но об этом в разделе 5. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 348. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (3.1)
(3.1) (3.2)
(3.2) млн. рублей. Поскольку объем финансирования ограничен и равен 5500 млн. рублей, то получаем ограничение
млн. рублей. Поскольку объем финансирования ограничен и равен 5500 млн. рублей, то получаем ограничение (3.3)
(3.3)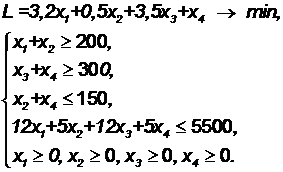 (3.4)
(3.4)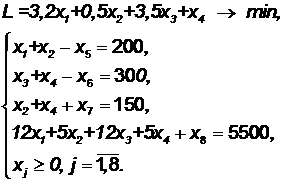


 (3.5)
(3.5)



 - «новый» разрешающий элемент, r - «старый» разрешающий элемент.
- «новый» разрешающий элемент, r - «старый» разрешающий элемент. .
. - «новый» элемент разрешающей строки, s - «старый» элемент разрешающей строки.
- «новый» элемент разрешающей строки, s - «старый» элемент разрешающей строки.
 - «новый» элемент ведущего столбца, t - «старый» элемент ведущего столбца.
- «новый» элемент ведущего столбца, t - «старый» элемент ведущего столбца. - «новый» элемент таблицы. Тогда он находится по формуле
- «новый» элемент таблицы. Тогда он находится по формуле
 β
β
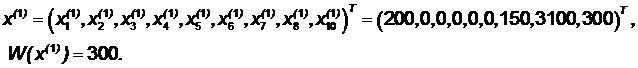
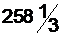

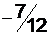









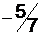


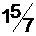










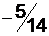


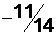
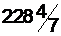

 млн. рублей.
млн. рублей.