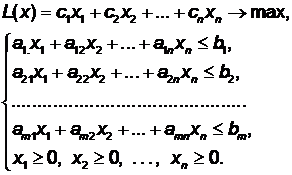ПРИМЕРЫ ФОРМАЛИЗАЦИИ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Задача о распределении ресурсов (или производственная задача)

Имеется m видов ресурсов (под ресурсами понимается сырье, энергия, рабочее время, потребительский спрос и т.д.). Известны запасы каждого ресурса: b_i, i=1,...,m. Ресурсы можно использовать для выпуска n видов продукции. Известна прибыль от выпуска единицы каждого вида продукции: c_j, j=1,...,n. Известны расходы каждого ресурса на единицу каждого вида продукции: a_{i j} , i=1,...,m,  j=1,...,n; здесь a_ij - расход i-го ресурса на выпуск единицы j-го вида продукции (возможно, что некоторые коэффициенты a_{i j} равны 0, если i-ый ресурс для выпуска j-ой продукции не используется). Требуется составить оптимальный план производства, т.е. найти, сколько продукции каждого вида требуется выпускать, чтобы получить максимальную прибыль (при соблюдении ограничений на ресурсы).

 Введем в рассмотрение неизвестные переменные x₁, x₂, …, x_n. Переменная x_j  будет обозначать план выпуска продукции j-го типа, . Тогда c_jx_j – ожидаемая прибыль предприятия от реализации продукции j-го типа, выражение

с₁x₁ +c₂x₂ + . . . +c_nx_n

представляет собой общую прибыль предприятия от реализации всей продукции, произведенной в соответствии с планом x₁, x₂, …, x_n. Максимизации прибыли – цель настоящей задачи. Поэтому можно записать целевую функцию:

L(x)= с₁x₁ +c₂x₂ + . . . +c_nx_n→max.

Сформулируем ограничения, вытекающие из постановки задачи.

Во-первых, для производства продукции используется сырье, запасы которого небезграничны. Рассмотрим более подробно первый вид сырья. a₁₁ – норма расхода этого сырья на производство единицы (штуки, килограмма, литра и т.п.) продукции первого вида. Поэтому a₁₁x₁ – расход сырья 1-го вида на весь выпуск продукции 1-го вида. Аналогично a₁₂x₂ – расход сырья 1-го вида на выпуск продукции 2-го вида, a₁₃x₃ – 3-го вида и т.д. Для реализации всего плана x₁, x₂, …, x_n выпуска продукции потребуется

a₁₁x₁ + a₁₂x₂ + . . . + a_1nx_n

единиц сырья 1-го вида. Естественно эта величина не может превосходить b₁ – количества сырья 1-го вида, имеющегося в запасах у предприятия. Т.о. возникает ограничение

a₁₁x₁ + a₁₂x₂ + . . . + a_1nx_n ≤ b₁.

Рассуждая подобным образом для 2-го, 3-го, . . . , n-го вида сырья, получим ограничения

a₁₁x₁ + a₁₂x₂ + . . . + a_1nx_n ≤ b₁,

a₂₁x₁ + a₂₂x₂ + . . . + a_2nx_n ≤ b₂,

. . . . . . . . . . . . . . . . . . . . . . . . .

a_m1x₁ + a_m2x₂ + . . . + a_mnx_n ≤ b_m.

Во-вторых, необходимо учесть, что искомые переменные не могут принимать отрицательных значений, т.е.

x₁ ≥0, x₂ ≥0, . . . , x_n ≥0.

Таким образом, окончательно математическая модель задачи принимает вид:

В задачу о распределении ресурсов часто входят и другие ограничения. Например, если задано условие, что изделий k-го вида необходимо выпустить не менее s_k единиц, то вводится следующее ограничение:

x_k >= s_k.

 Если задано, что изделия видов p и q должны выпускаться в соотношении s_p / s_q , то вводится следующее ограничение:

x_p/ x_q = s_p/ s_q,

которое приводится к стандартной форме следующим образом:

s_q  x_p – s_p  x_q = 0.